Thu Nov 27 2025 00:00:00 GMT+0800 (中國標準時間)
MLO(Multi-level Optimization)
迭代循环:$i$层的最优参数作为$i+1$层的输入
- 第一级:固定生成模型架构,在 GAN 框架下训练生成器和判别器,生成逼真图像。
- 第二级:用生成的图像 - 掩码对 + 少量真实数据,训练分割模型。
- 第三级:以分割模型的验证损失为目标,优化生成模型的架构,形成迭代闭环。
框架
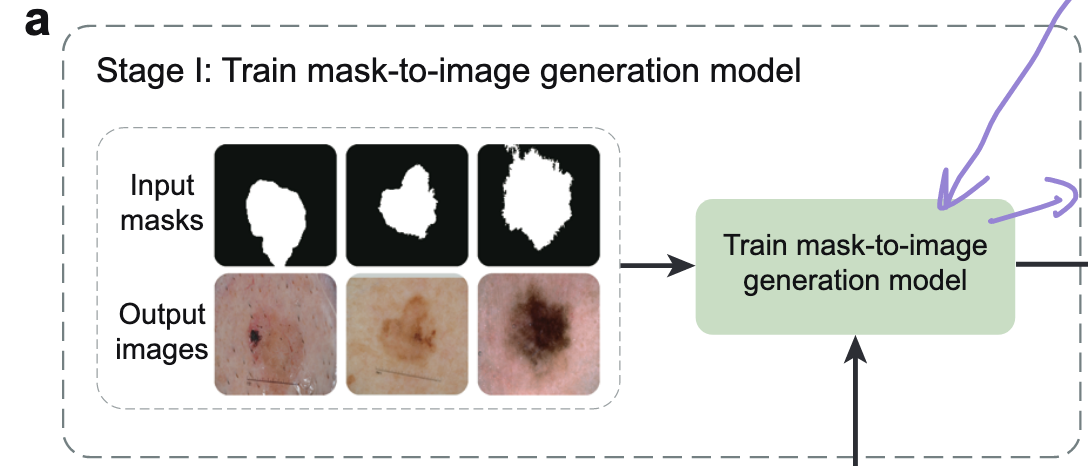
Stage1️⃣:训练 图像生成器(固定架构,先练参数)
- 目标:让生成模型先学会 “根据掩码生成看起来像真实医学图像的图片”,但此时不优化生成模型的架构(仅固定架构 A,练权重参数 G 和判别器 H)。
- 操作:
- 把真实的 “图像 - 掩码对” 反过来用:以真实掩码 M 为输入,真实图像 I 为目标,构建 GAN 的训练数据集(M→I 的映射)。
- 在 GAN 框架下训练:判别器 H 学 “区分真实图像和生成图像”,生成器 G 学 “骗过分判别器”,最终生成器能输出与掩码语义对齐的逼真图像(比如输入 “皮肤病变掩码”,生成对应 dermoscopy 图像)。
- 关键衔接:这一步的生成器参数(G*)会传给第二级,作为生成 “辅助训练数据” 的基础。
这个反过来使用比较有趣:真实人工标注掩码—>图像增强—>生成增强后掩码—>通过生成模型,生成医学图像。
其中“图像增强”有什么用?增强后的掩码与原掩码有何区别?
这个地方使用的是GAN,算是比较老的方法了。
GAN结构中生成模型
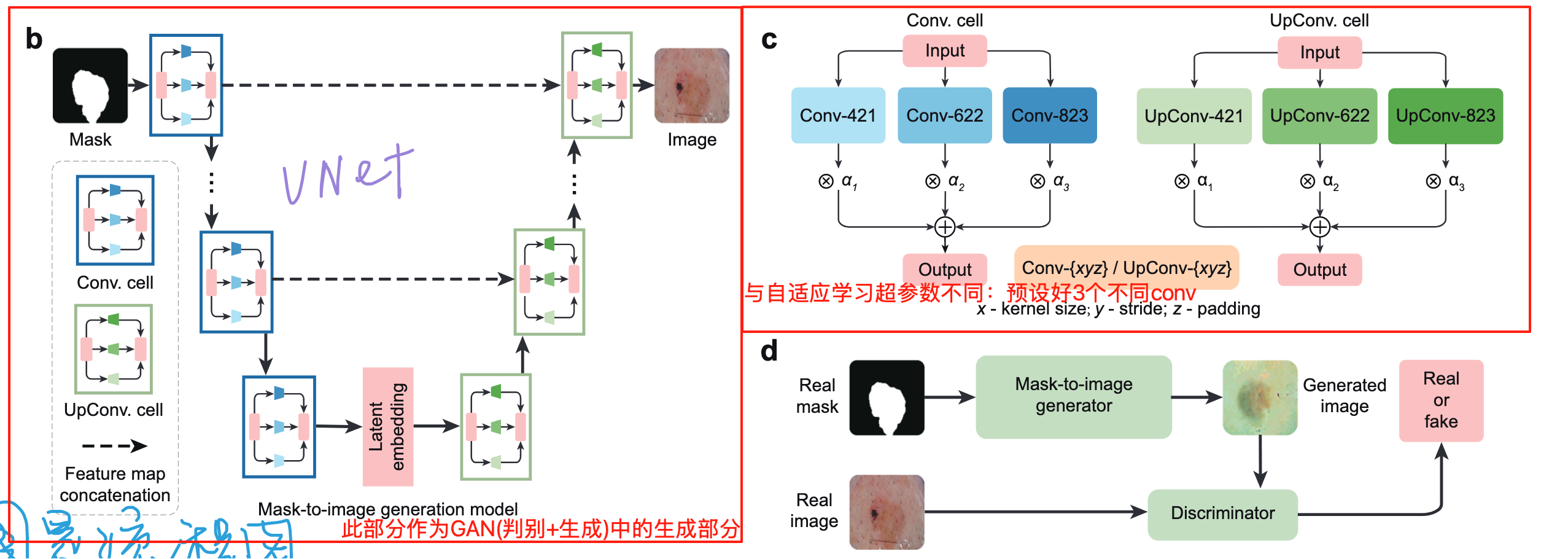
Stage2️⃣:用 生成数据 + 少量真实数据训练分割模型
目标:检验第一级生成的数据是否 “有用”—— 如果生成数据质量高,用它训练的分割模型在真实验证集上表现会好(对应你选中的 “验证性能反映生成数据质量”)。
损失函数:普通的GAN contrastive loss: “最大化区分真实图像和生成图像的损失”
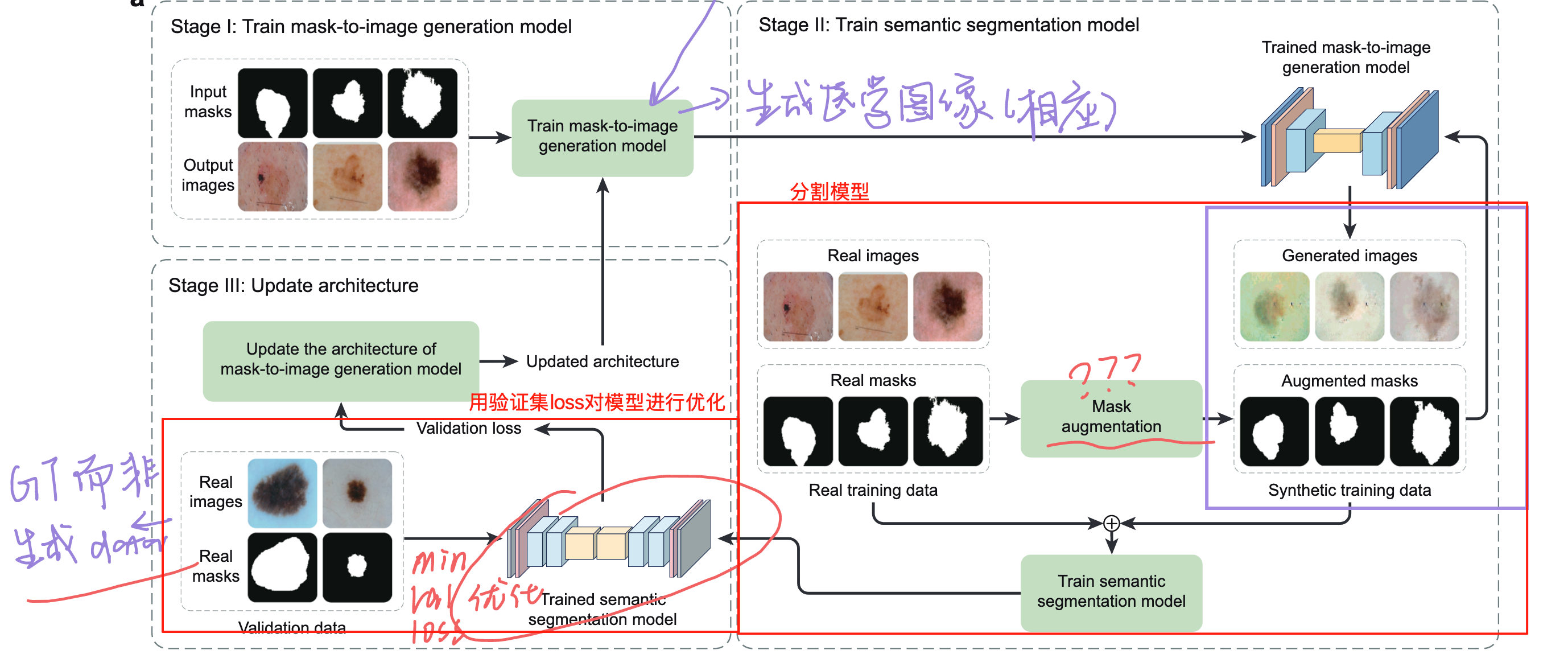
操作:
- 生成辅助数据:用第一级训好的生成器,对真实掩码做基础增强(旋转、翻转等),生成大量 “合成图像 - 合成掩码对”((\hat{I},\hat{M}))。
- 混合训练:把 “合成数据 + 少量真实数据” 一起喂给分割模型(如 UNet/DeepLab),用分割损失(像素级交叉熵)训练分割模型参数 S。
- 验证反馈:用真实医学图像 + 专家标注掩码组成的验证集,评估分割模型的性能(Dice/Jaccard)—— 如果性能差,说明生成数据质量低,需要优化生成模型。
关键衔接:这一步的分割模型验证损失((L_{seg}^{val}))会传给第三级,作为优化生成模型架构的 “信号”。
Stage3️⃣:用分割验证损失,调Stage1️⃣架构
🫵:Stage2️⃣的训练下降是计算的DICE Loss。Val验证集上的结果只能看。
- 目标:解决 “第一级固定架构可能不适配分割任务” 的问题 —— 比如某些架构生成的图像 “看起来真,但对分割模型没用”(比如生成了过多背景噪声,反而干扰病变分割),这一步通过分割验证损失优化架构 A。
- 操作:
- 把第二级的 “分割模型验证损失” 作为优化目标:最小化这个损失(即让分割模型在真实验证集上表现更好),反向调整生成模型的架构 A(比如选择更适合的卷积核大小、激活函数组合)。
- 迭代闭环:架构 A 优化后,重新回到第一级(用新架构 A 再训生成器参数 G),重复 1→2→3,直到分割模型性能收敛。
实验
1. 对各数据集的分割性能进行展示
图2/3/4:2/3展示结果,4展示以少量的数据就可以获得好的分割结果。
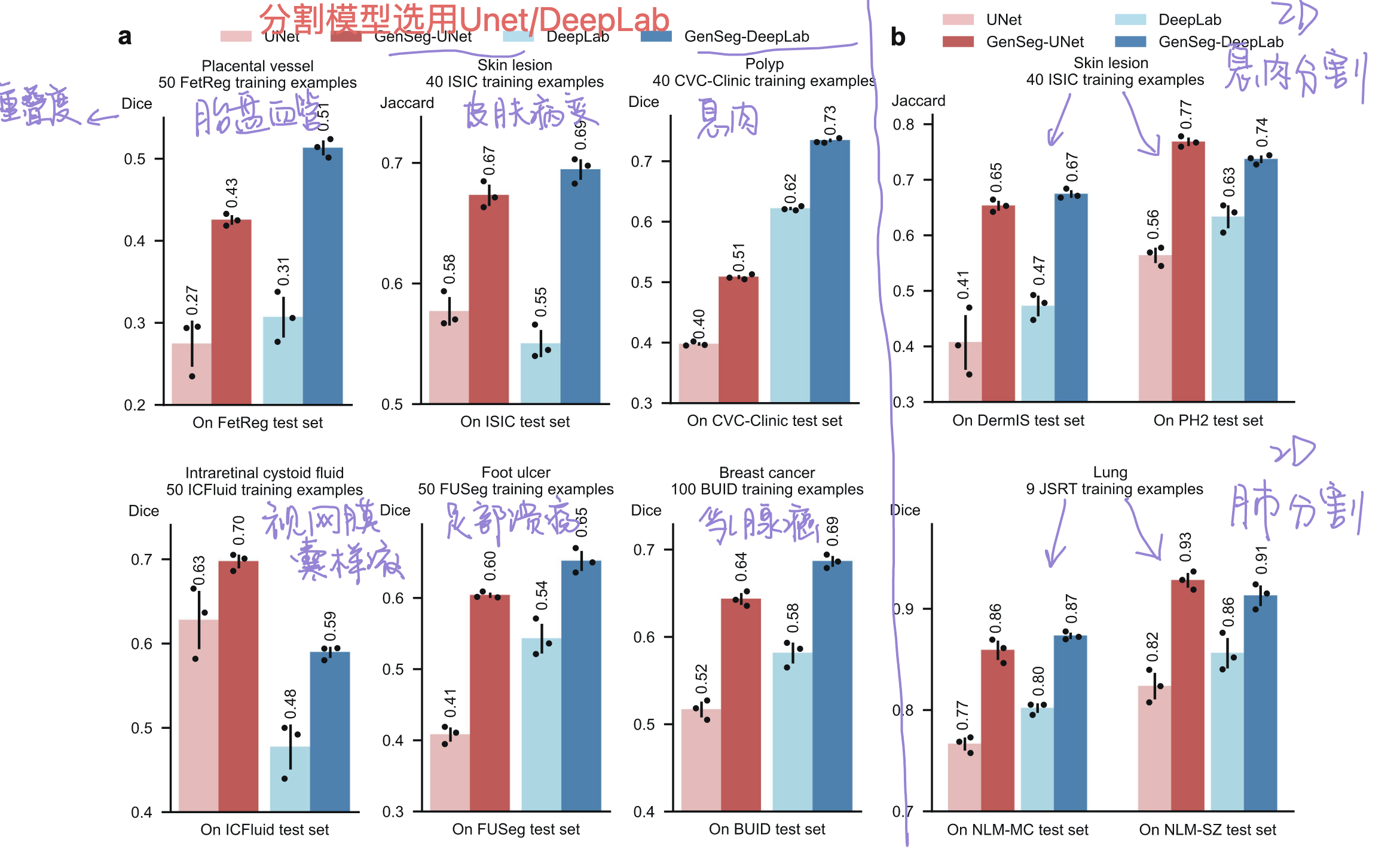
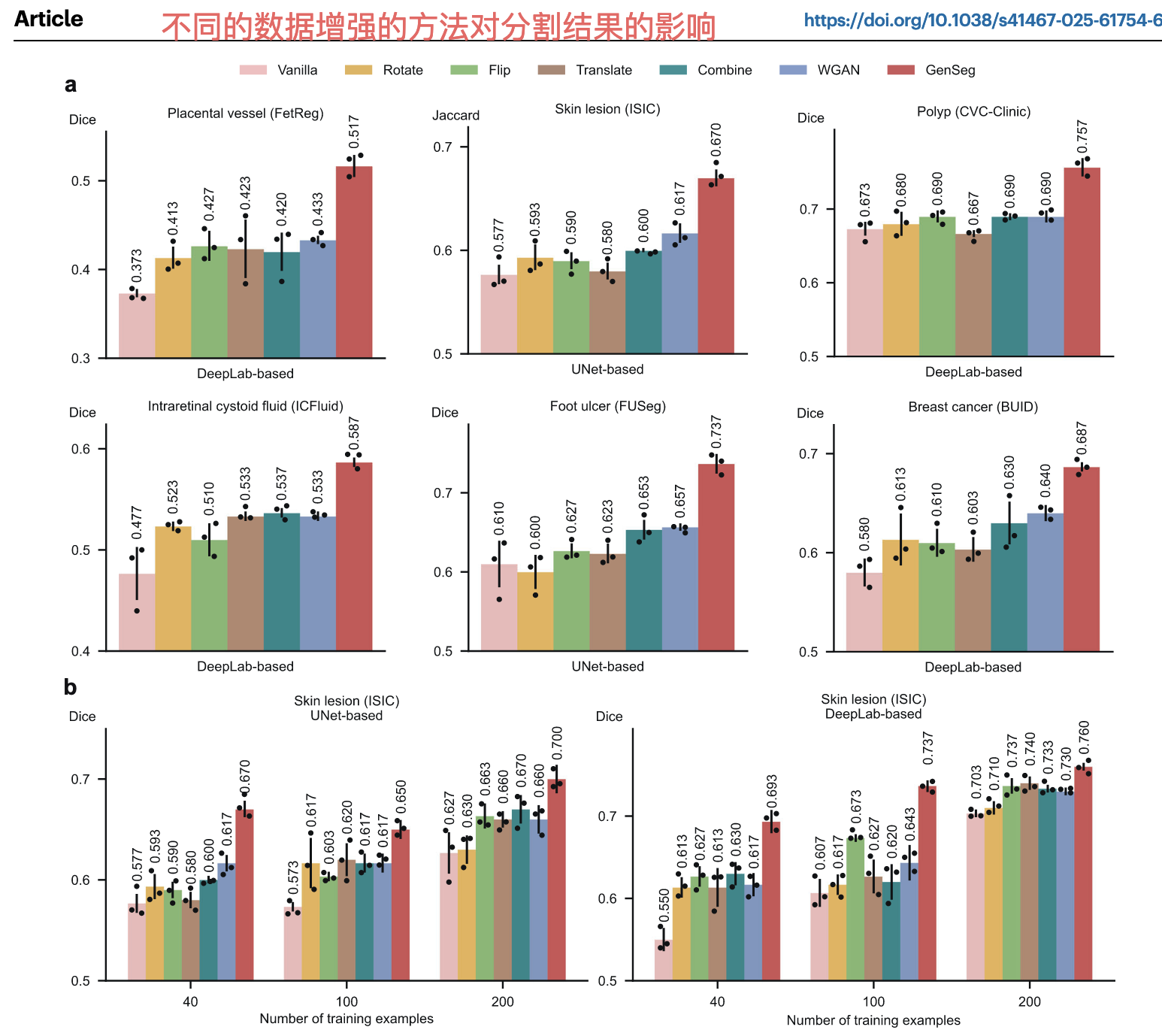
2.对比传统数据增强
目的:医学分割中的常见数据增强方法是旋转、翻转、平移及组合(实际临床研究 / 应用中最易获取的提升方法)。证明方法比这些数据增强方法更有效。
我的疑问
- 要是我的理解没错的话,这个步骤是,先训练图片生成模型GAN,其损失函数是contrastive loss,也就是生成/判别之间的差异;然后得到暂时最优的图片生成模型,以其输出作为训练分割模型的输入,以预测分割与mask之间的差异来优化下降(DICE loss),得到一个最优的分割模型,这个分割模型将在val验证集上计算得到一个loss结果,根据这么一个loss结果,再去优化下降修改生成模型的结果?那么这样的流程不是非常复杂,而且势必会训练得非常慢,而且难以收敛吗?因为为了每得到一个val loss,我都要完整训练两个模型?
对于MLO的理解问题。多水平优化(MLO)不是 “完整训练两个模型再循环”,而是 “增量迭代 + 梯度近似” ,本质是 “小步微调” 而非 “推倒重来”。
- 医学分割与食品计算的区别?医学分割得益于人类具有各种各样的器官以及不同的疾病,所以可以针对每种疾病/器官收集数据,而且这每个数据集都是有用的,因为可以 识别人类的一种疾病。(这如同医院会针对每个身体部位设计不同的科室,但是对于食物就只有营养科),我想知道的是,能不能拔高做食品的意义?如何类推?
| 指标名称 | 英文全称 | 数学公式 | 符号说明 |
|---|---|---|---|
| 均方误差 | Mean Squared Error (MSE) | (MSE = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2) | (y_i):第 i 个样本的真实值;(\hat{y}_i):第 i 个样本的预测值;n:样本总数 |
| 均方根误差 | Root Mean Squared Error (RMSE) | (RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2}) | 同 MSE,为 MSE 的平方根,还原误差的量级维度 |
| 平均绝对误差 | Mean Absolute Error (MAE) | $MAE = \frac{1}{n}\sum_{i=1}^n\vert y_i - \hat{y}_i\vert$ | 同 MSE,采用绝对值计算,降低异常值对误差评估的影响 |
| 平均绝对百分比误差 | Mean Absolute Percentage Error (MAPE) | $MAPE = \frac{1}{n}\sum_{i=1}^n \left\vert\frac{y_i - \hat{y}_i}{y_i} \right\vert\times 100\%$ | 同 MSE,以真实值为基准计算相对误差,需满足(y_i \neq 0) |
| 决定系数 | Coefficient of Determination (R²) | (R^2 = 1 - \frac{\sum_{i=1}^n (y_i - \hat{y}_i)^2}{\sum_{i=1}^n (y_i - \bar{y})^2}) | (\bar{y}):所有样本真实值的均值,衡量模型对数据的解释力 |
| 相关系数 | Correlation | (Correlation = \frac{\sum_{i=1}^n (y_i - \bar{y})(\hat{y}_i - \hat{\bar{y}})}{\sqrt{\sum_{i=1}^n (y_i - \bar{y})^2} \sqrt{\sum_{i=1}^n (\hat{y}_i - \hat{\bar{y}})^2}}) | (\hat{\bar{y}}):所有样本预测值的均值,衡量真实值与预测值的线性关联强度 |
| 中位数相对误差 | Median Relative Error (Median_RE) | $Median_RE = median\left( \left\vert\frac{y_i - \hat{y}_i}{y_i} \right\vert\times 100\% \right)$ | 取相对误差的中位数,进一步降低极端值干扰,更稳健反映模型误差水平 |
现在我有一个方法,叫MCMoE,其相关的代码放在:/Users/schwertlilien/Downloads/test/MCMoE-main的文件夹中。我现在想使用这个方法在我的三模态数据上运行一个回归任务,对毒素进行预测。至于三模态的参考数据集你可以参考/Users/schwertlilien/Downloads/test/multimodalDataset.py。我要怎么做才能在这个方法上训练我的数据集?
why diffusion models …
Epoch: 70 Loss: 0.0466 Train Coef: 0.703 Test Loss: 215125910877.9747 Test Coef: 0.829 R²: 0.5416 RMSE: 463816.65 MAE: 280875.84 MAPE: 2708.91%
warnings.warn(warn_msg)
Epoch: 119 Loss: 0.0438 Train Coef: 0.742 Test Loss: 165065224606.7848 Test Coef: 0.921 R²: 0.6483 RMSE: 406282.22 MAE: 172450.53 MAPE: 1140.81%
1 | graph LR |