2025-4-13-再探DeepSeek之MLA+MoE

4/16：

感觉MoE此处还得修修补补。

4/15:

写了两天了，尊嘟很长。顺便diss一下下面的三篇blog。虽然算是比较偏算法讲解部分，但是还是有错误的。比如：

感觉都存在一定的问题。我上方圈画出来的部分中，比如说：

1. “低秩矩阵”指代不明，若是指的是$W^{UK},W^{UV}$，但是这个又不是用来降维用的；或许只是指明这两个矩阵的秩比较低？？好奇怪，不如说是维数比较低的矩阵。
2. 如果指的是$W^{UK},W^{UV}$的话，二者的维度是$d\times d_c$.
3. 这个错的比较明显：就是$W^{DQ}\in\mathbb{R}^{d_c’\times d},W^{UQ}\in\mathbb{R}^{d_hn_h\times d_c’},W^{QR}\in \mathbb{R}^{d_h^Rn_h\times d_c’}$.

4/13:

推荐三篇博客，看完之后感觉自己什么都不懂（）

只能说要学的东西还是太多了orz orz orz orz orz orz

deepseek技术解读(1)-彻底理解MLA（Multi-Head Latent Attention）

deepseek技术解读(2)-MTP（Multi-Token Prediction）

deepseek技术解读(3)-MoE的演进之路

基本上包含上述的内容+自己理解+补充内容

DeepSeek-MoE

DeepSeek MoE 是 Transformer 架构中的部分，其核心改进在于用 MoE 层 替代了标准的 FFN（Feed-Forward Network）。架构如下。

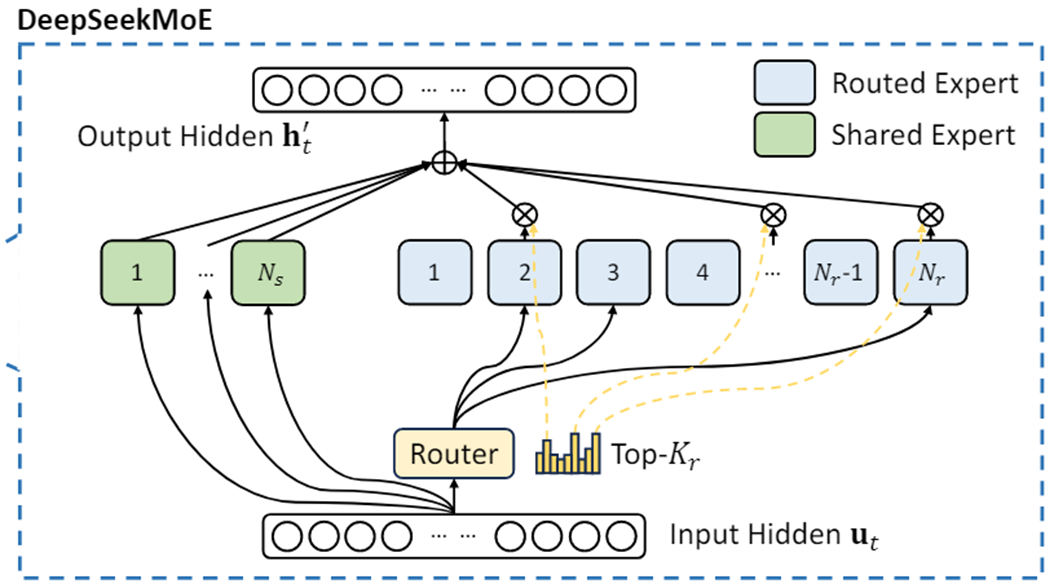
相较于普通的MoE有何区别？值得注意的是，在这三种体系结构中，专家参数的数量和计算成本保持不变。

• 子图(a)展示了具有传统top-2路由策略的MoE层。
• 子图(b)说明了细粒度专家分割策略。
• 子图(c)展示了共享专家隔离策略的集成，构成了完整的DeepSeekMoE架构。

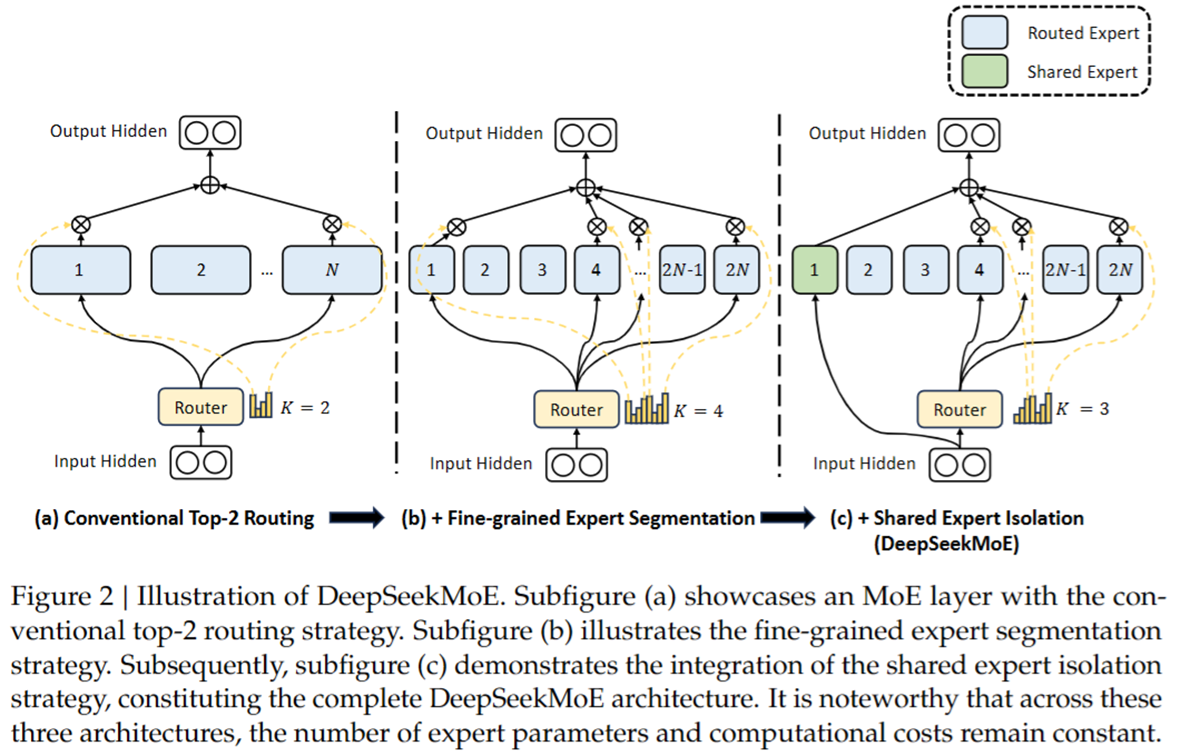
输入：Token Embeddings（词嵌入向量）：经过 Self-Attention 计算后的隐藏状态（hidden states），维度通常为 [batch_size, seq_len, hidden_dim]。对于共享专家直接输入，而走普通专家，则需要先经过 路由（Router） 机制，决定哪些专家（Expert）参与当前 token 的计算。

输出：加权专家输出的组合。每个 token 会被分配给 少数几个专家（如 Top-2），它们的输出按权重组合后，形成最终的输出，维度仍为 [batch_size, seq_len, hidden_dim]。

方面	说明
输入	Token 经过 Self-Attention 后的隐藏状态
输出	由部分专家组合计算的加权输出
MoE 结构	多个专家 + 路由机制，稀疏激活
优势	计算高效、模型容量大、任务适应性强
替代 FFN	FFN 计算密集，MoE 实现动态计算
专家含义	自动学习不同技能，可能对应不同任务模式

每个专家代表什么？

MoE 中的 专家（Expert） 并不是人为设定的，而是在训练过程中 自动学习不同的特征或技能。可以类比为：

• 隐式的专业化分工：
  • 某些专家可能擅长 数学推理。
  • 某些专家可能擅长 代码生成。
  • 某些专家可能擅长 自然语言理解。
• 自动路由机制：
  • Router 会根据输入 token 的语义，自动选择最相关的专家组合。
  • 例如，数学问题可能激活 擅长逻辑推理的专家，而代码生成可能激活 擅长结构化输出的专家。

专家是否真的具有可解释性？

• 部分可解释：一些研究发现，MoE 模型的专家会倾向于处理特定类型的数据（如代码、数学等）。
• 但并非绝对：由于是自动学习，专家的分工可能是 隐式 的，不一定严格对应人类可理解的类别。

例子

假设我们有一句话： “猫喜欢吃鱼，但狗更喜欢啃骨头。” 模型需要处理这句话的每个词（token），并生成对应的语义表示。

FFN处理

在标准 Transformer 中，每个词 都会经过 同一个 FFN 进行计算，就像所有学生（token）都必须听 同一个老师（FFN） 讲课，无论他们是否需要这个知识。

• 输入序列（假设每个词已编码为向量）：
  [猫, 喜欢, 吃, 鱼, 但, 狗, 更, 喜欢, 啃, 骨头]
• FFN 的工作方式：
  • 每个词（如 猫、鱼、狗、骨头）都经过 完全相同的全连接层。
  • 即使 猫 和 鱼 是动物相关词，啃 和 吃 是动作词，它们用的却是 同一套参数，缺乏 specialization（专业化）。

问题：

• 计算量大：所有词都经过 FFN，即使有些计算是冗余的。
• 模型容量受限：FFN 参数固定，难以同时学好不同领域的知识（如动物、动作、对比关系）。

MoE（混合专家）处理

MoE 用 多个专家（Experts） 替代单一 FFN，并引入 路由机制（Router），动态决定每个词由哪些专家处理。 假设我们有以下专家（实际是自动学习的，这里仅举例）：

专家编号	可能擅长的领域（模型自动学习）
Expert 1	动物相关词汇（猫、狗、鱼、骨头）
Expert 2	动作相关词汇（吃、啃、喜欢）
Expert 3	逻辑关系（但、更）
Expert 4	通用词汇（其他）

MoE 的工作流程：

1. 路由（Router）决定分配：对每个词，Router 计算它属于各个专家的概率（如 猫 → 80% Expert 1, 10% Expert 2, 5% Expert 3, 5% Expert 4）。选择 概率最高的 2 个专家（Top-2 Routing，常见设定）。
2. 专家计算：每个词仅由 被选中的专家 处理，其他专家不参与计算（稀疏激活）。
3. 加权组合输出：选中的专家输出按路由权重相加，得到最终表示。

DeepSeekMoE: Route Expert+Shared Expert.共享专家（Shared Expert）的作用类似于一个“全能替补队员”，它既能为特定领域提供辅助支持，又能保证通用知识的覆盖，避免某些token因路由分配不均而“无人处理”。

共享专家是MoE层中一个或多个被所有token共享的专家，无论路由如何分配，它都可能以一定概率参与计算。它不像其他专家那样高度专业化，而是具备通用知识，起到“兜底”作用。

猫 和 鱼 主要由 动物专家（Expert 1） 处理，而 吃 和 啃 主要由 动作专家（Expert 2） 处理。

词（Token）	可能被分配的专家（Top-2）	计算方式
猫	Expert 1（动物） + Expert 4（通用）	由动物专家主导
吃	Expert 2（动作） + Expert 1（动物）	由动作专家主导
鱼	Expert 1（动物） + Expert 4（通用）	由动物专家主导
但	Expert 3（逻辑） + Expert 4（通用）	由逻辑专家主导
狗	Expert 1（动物） + Expert 4（通用）	由动物专家主导
啃	Expert 2（动作） + Expert 1（动物）	由动作专家主导

MoE 相比 FFN 的优势

特性	标准 FFN	MoE
计算方式	所有 token 使用相同的 FFN	每个 token 只激活部分专家
参数效率	参数固定，计算全部激活	参数更多，但计算量可控（稀疏激活）
模型容量	受限于单一 FFN 的尺寸	可扩展（增加专家数量不影响计算量）
训练/推理效率	计算量随模型尺寸线性增长	计算量可控（仅激活部分专家）

MLA

MLA主要是为了减少KV的内存消耗，那么首先想要对LLM中KV占比有一个概念。

LLM模型推理过程

1. Prefill 阶段
   • 给定一段输入 prompt（共 N 个 token），模型一次性并行地处理这 N 个 token，生成第一个输出 token（第 N+1 个 token）的 logits。
   • 这个阶段的注意力计算是全并行的，注意力矩阵是 [N x N]，即每个 token 都能关注 prompt 中的所有 token。
2. Decode 阶段
   • 从第 N+1 个 token 开始，每次只生成一个 token。每一步的输入是之前已经生成的所有 token。
   • 由于自回归的限制，每生成一个 token 都需要依赖前面所有 token 的上下文，导致计算无法并行，每一步必须等待上一步完成。
   • 注意力计算是 [1 x (N + i - 1)]，即当前 token 需要关注前面所有的 token。

LLM基于Transformer，从decoder的结构我们可知：第$t$个token的输出，需要使用Q与前面$1\sim t-1$位置的K,V计算：

1. 计算前面的K,V不受后续的token的影响。（因此可以缓存）
2. 后面计算$t+1\sim N$的tokens，都需要与前面$1\sim t-1$位置的K,V计算。（K,V出现冗余）

Q: 所有的LLM都是基于Transformer的吗？

A: 几乎所有主流 LLM 都是基于 Transformer 架构的，尤其是 decoder-only Transformer。

KV-cache机制

目前主流的KV-cache机制：将前序计算好的KV缓存起来。

缺点：空间换时间。GPU显存也很宝贵。

换句话说:

• 如果不用KV-cache模型直接计算（重复计算前序K,V），是个计算密集型任务；
• 增加了KV-cache，现在K,V不是通过计算得到，而是从「存储介质」里读出来，GPT内核与存储介质之间要频繁读写，这样就变成了一个访存密集型任务。

所以使用了KV-cache的机制，解决的重复计算的问题，但访存的速率也就直接影响到训练和推理的速度。

LLM推理阶段显存使用情况

访存速率分级

由下图的访存带宽可知，卡内的带宽是单机卡间的带宽的3倍，是跨机带宽的20倍，所以我们对于存储的数据应该优先放到卡内，其次单机内，最后可能才考虑跨机存储。

在GPU上部署模型的原则是：能一张卡部署的，就不要跨多张卡；能一台机部署的，就不要跨多台机。这是因为“卡内通信带宽 > 卡间通信带宽 > 机间通信带宽”，由于“木桶效应”，模型部署时跨的设备越多，受设备间通信带宽的的“拖累”就越大

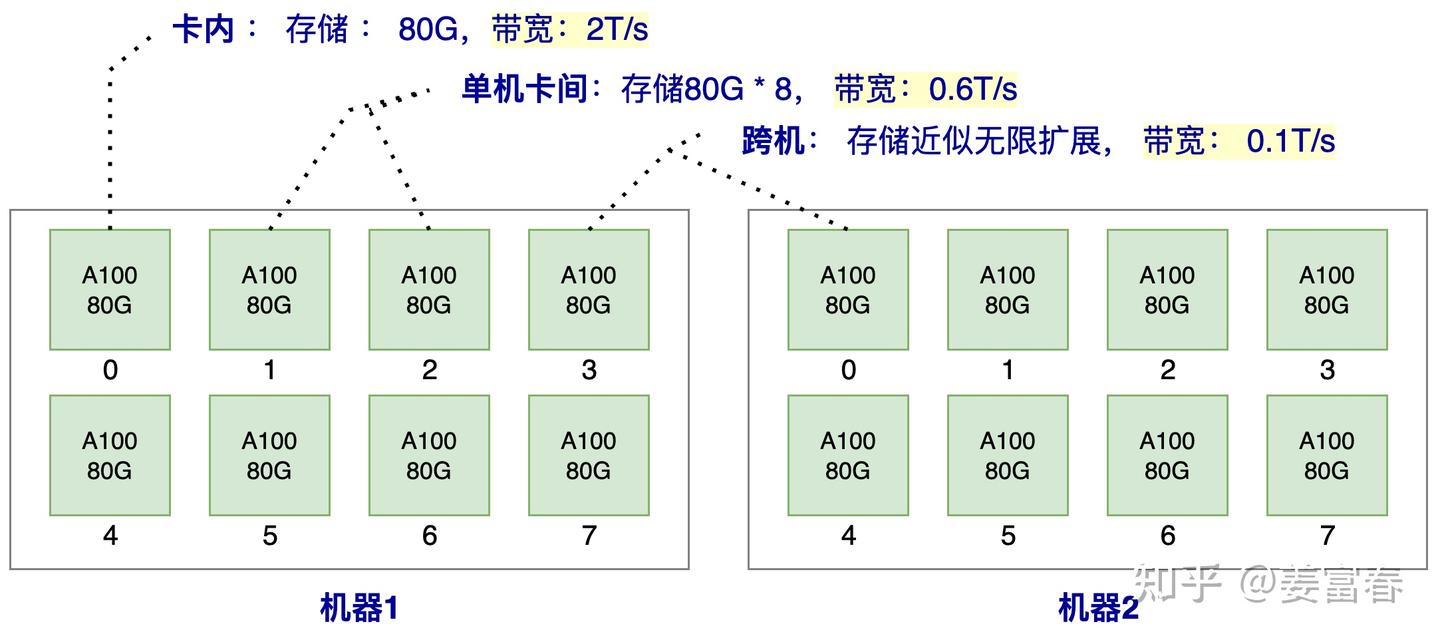
【到了熟悉的计组时间(>v<) !】

通用的GPU的存储介质除了显存，还有SRAM（Static Random Access Memory）/DRAM（Dynamic Random Access Memory），二者是一个“速度-容量-成本”之间的权衡组合。

• SRAM 快但贵，用来加速
• DRAM 慢但大，用来存储

特性	SRAM	DRAM
类型	静态随机存储	动态随机存储
是否需刷新	否	是
速度	快（低延迟）	慢（高延迟）
成本	高	低
密度	低	高
容量	小（KB~MB）	大（GB 级）
常见用途	Cache、寄存器、Shared Memory	显存（GDDR/HBM）、主存（DDR）
GPU 中的体现	L1/L2 Cache, Registers, Shared Mem	Global Memory, 显存

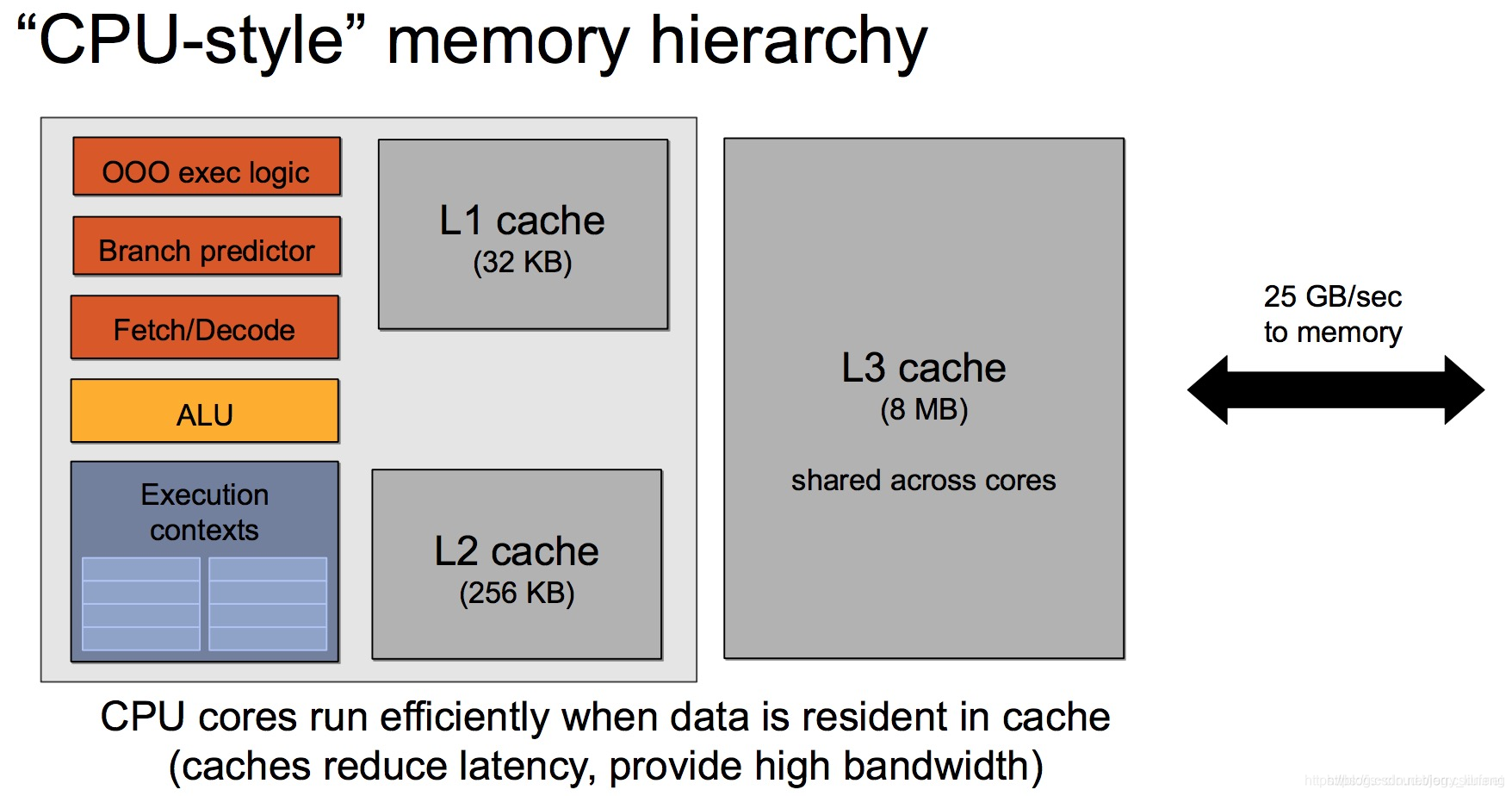
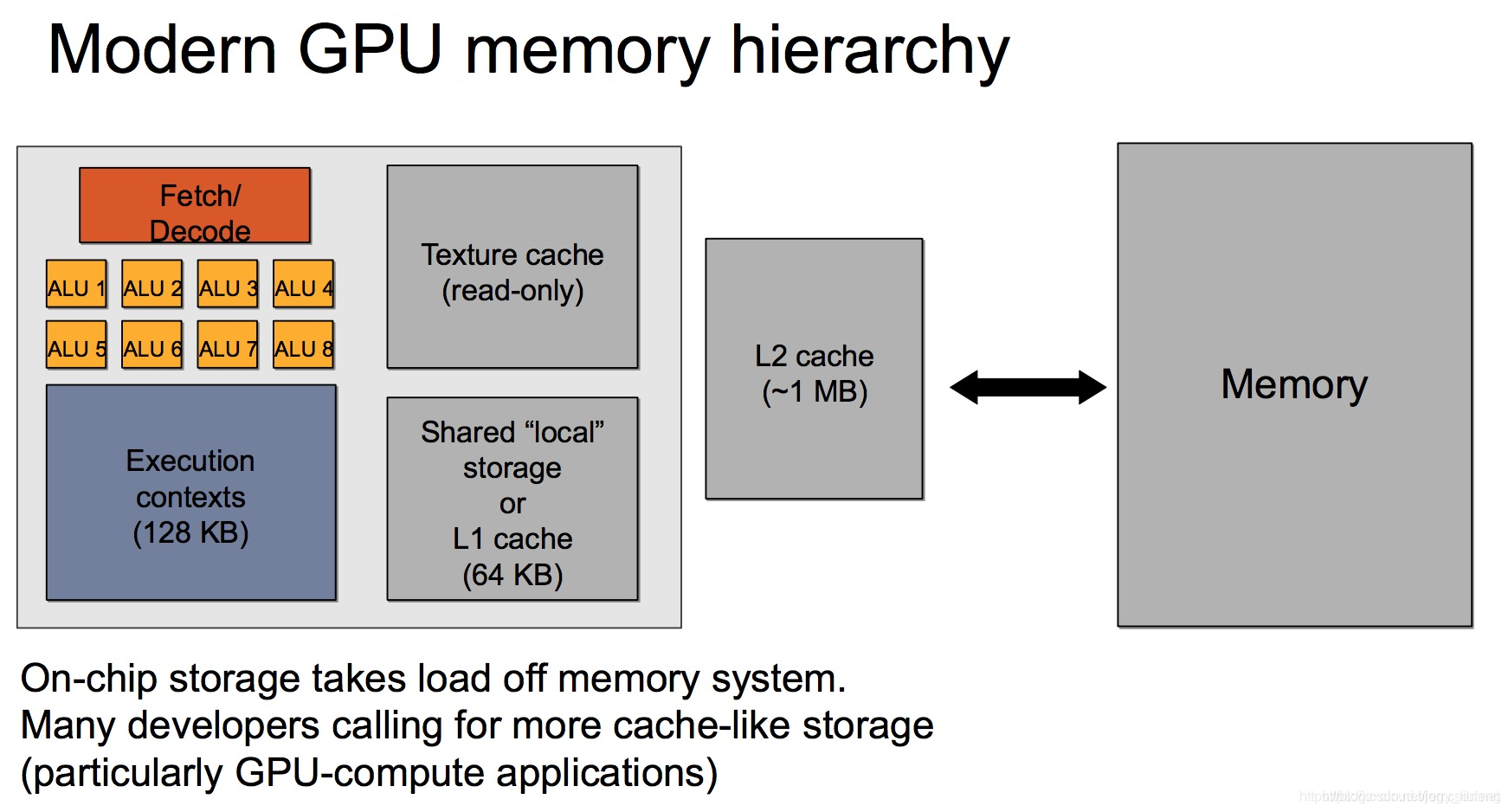
Q: 话说回来，不同厂家的GPU的内部架构都不同，所以呢？？

A: 不同厂商（比如 NVIDIA、AMD、Apple、Google TPU、华为昇腾）在 GPU 或 AI 加速器上的 架构设计差异巨大，但在存储层级的设计上，确实存在一个“通用范式”：由快而小的 SRAM（如 Registers、Shared Memory、L1/L2 Cache）构成近端缓存层，由慢而大的 DRAM（如 Global Memory 或 HBM）构成主存层。

通用 GPU 存储层级（从快到慢）：

存储层级	类型	作用	典型介质	延迟/带宽	容量级别
寄存器	SRAM	单个线程/线程组的局部变量	SRAM	极低/极高	KB/线程组
Shared Memory / Local Data Store	SRAM	一个线程块/工作组共享	SRAM	极低/高	64~128KB
L1 Cache	SRAM	核心级缓存	SRAM	低	~128KB
L2 Cache	SRAM	多核心共享缓存	SRAM	中	数 MB
Global Memory / 显存	DRAM	所有线程可访问的数据区	GDDR / HBM	高	GB 级
Host Memory	DRAM	主机 RAM（通过 PCIe/NUMA）	DDR4/5	非常高	多 GB

---

不同厂商的差异主要体现在：

厂商	特点或差异化设计
NVIDIA	CUDA 架构明确划分 Registers、Shared Memory、L1/L2、Global Memory。Ampere 开始用 HBM。
AMD	ROCm 架构类似，使用 LDS（Local Data Store）等概念来等价 Shared Memory。
Apple M 系列	统一内存架构（UMA），CPU/GPU 共享物理内存，省去拷贝但牺牲带宽。
TPU (Google)	大量使用 on-chip SRAM，结构非 Transformer-like，但仍保有近似层级。
华为 昇腾 / 寒武纪	加入 AI Core Buffer，模型层输出缓存有定制优化。

尽管名称、调度方式不同，但它们都遵循“小而快的近端缓存 + 大而慢的远端主存”这一通用理念。

模型推理阶段显存分配

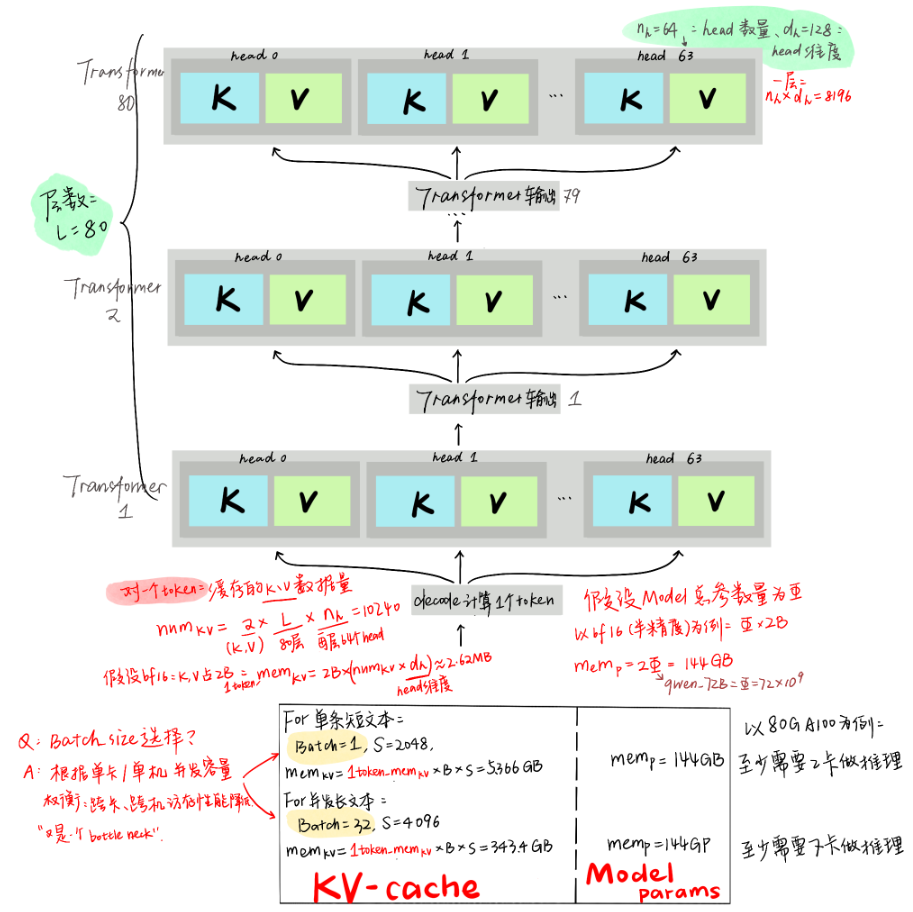
减少KV Cache的目的: 就是要实现在更少的设备上推理更长的Context，或者在相同的Context长度下让推理的batch size更大，从而实现更快的推理速度或者更大的吞吐总量。

推理阶段主要有三部分数据会放到显存里。

• KV Cache ： 如上一节所述，前序token序列计算的K,V结果，会随着后面tokent推理过程逐步存到显存里。存储的量随着Batch，Sequence_len长度动态变化。
• 模型参数：包括Transformer、Embedding等模型参数会存到显存里。模型大小固定后，这个存储空间是固定的。
• 运行时中间数据： 推理过程中产出的一些中间数据会临时存到显存，即用即释放，一般占用空间比较小。

因此，主要存储消耗是：KV cache和模型参数。

共享KV优化显存方法：MQA/GQA

• MQA（Multi-Query Attention）：每一层的所有Head，共享同一个K,V来计算Attention。相对于MHA的单个Token需要保存的KV数（ $2∗l∗n_h$ ）减少到了（ $2*l$ ）个，即每一层共享使用一个K向量和一个V向量。
• GQA（Group-Query Attention）：GQA是平衡了MQA和MHA的一种折中的方法。不是每个Head一个KV，也不是所有Head共享一个KV，而是对所有Head分组，比如分组数为 $g$ ，每组： $n_h/g$个Head 共享一个KV。
  • 当 $g=1$ 时，GQA就等价于MQA;
  • 当 $g=n_h$时， GQA就等价于MHA。

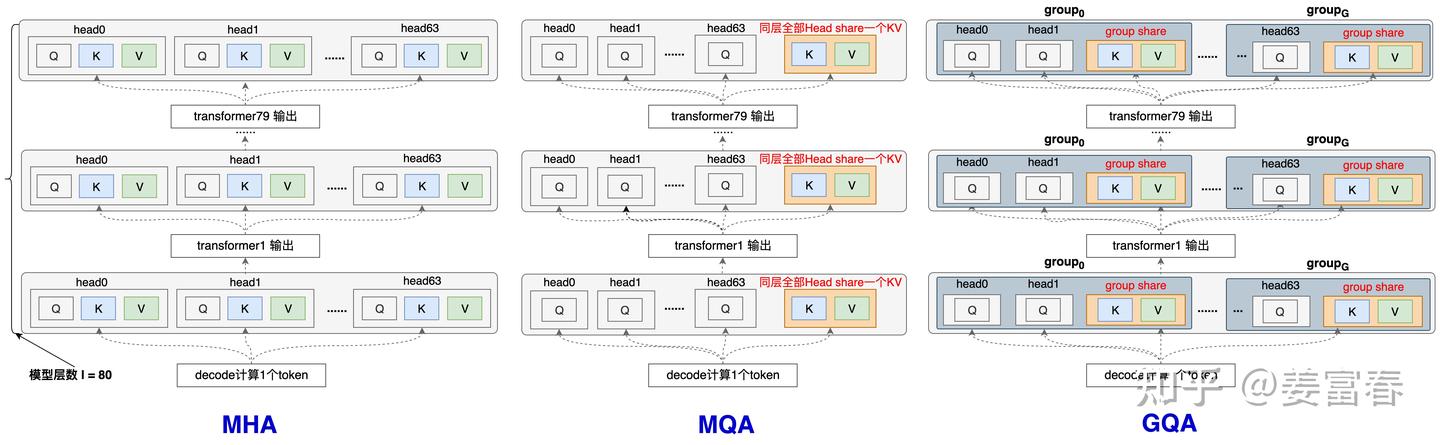
	KV cache缓存量
MHA	$2ln_h$
MQA	$2*l$
GQA	$2lg,1\le g\le n_h$

MLA优化KV-cache

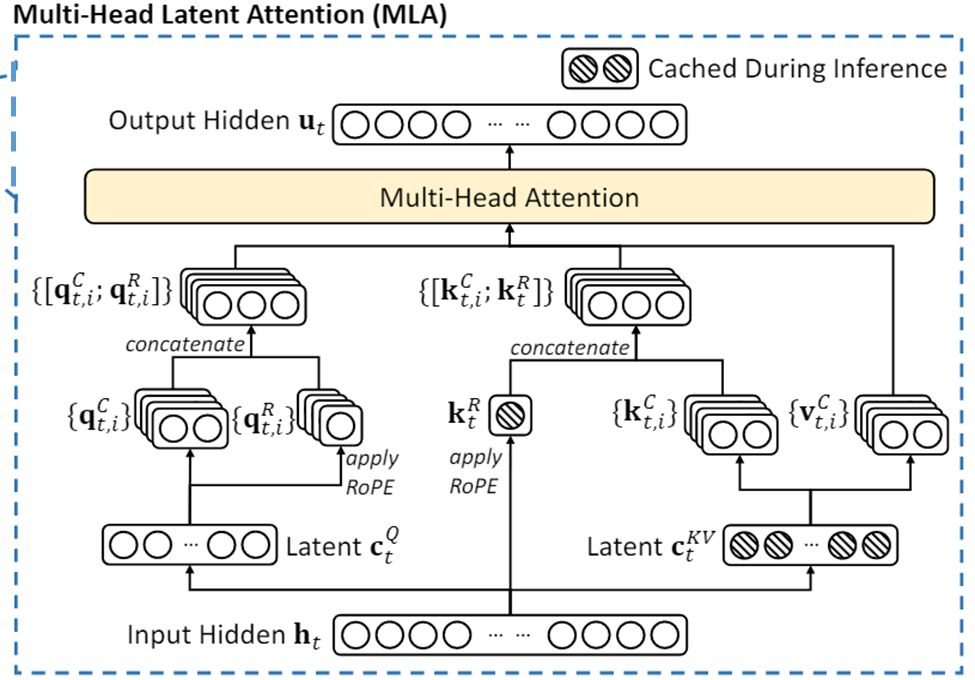
每个Transfomer层中，只缓存了$\mathbf{c}^{KV}_t,\mathbf{k}^R_t$:

• $\mathbf{c}^{KV}_t$: $dim=d_c=4*d_h=512$
• $\mathbf{k}^R_t$: $dim=d_h^R=d_h/2=64$

对比MQA（每层KV：$2d_h=256$），MLA相当于增加了2.25倍的存储。

Q: 但DeepSeek描述自己的方法不仅比MQA强，而且比非共享KV的原始MHA也要强，这是为什么？？

A: MLA具有恢复全K,V的能力。特征表达能力显著比GQA、MQA要强。

MLA 中 KV 的计算流程：通过低秩压缩 $\rightarrow$ 缓存一个小维度的中间变量 $\rightarrow$ 后续再恢复出完整维度的 $K$、$V$。

好，回到公式来看看到底为什么。

$$\begin{align*} \mathbf{c}_t^Q &= W^{DQ}\mathbf{h}_t, \tag{1}\\ [\mathbf{q}_{t,1}^C; \mathbf{q}_{t,2}^C; \cdots; \mathbf{q}_{t,n_h}^C] = \mathbf{q}_t^C &= W^{UQ}\mathbf{c}_t^Q, \tag{2}\\ [\mathbf{q}_{t,1}^R; \mathbf{q}_{t,2}^R; \cdots; \mathbf{q}_{t,n_h}^R] = \mathbf{q}_t^R &= \text{RoPE}(W^{QR}\mathbf{c}_t^Q), \tag{3}\\ \mathbf{q}_{t,i} &= [\mathbf{q}_{t,i}^C; \mathbf{q}_{t,i}^R], \tag{4}\\ \mathbf{c}_t^{KV} &= W^{DKV}\mathbf{h}_t, \tag{5}\\ [\mathbf{k}_{t,1}^C; \mathbf{k}_{t,2}^C; \cdots; \mathbf{k}_{t,n_h}^C] = \mathbf{k}_t^C &= W^{UK}\mathbf{c}_t^{KV}, \tag{6}\\ \mathbf{k}_t^R &= \text{RoPE}(W^{KR}\mathbf{h}_t), \tag{7}\\ \mathbf{k}_{t,i} &= [\mathbf{k}_{t,i}^C; \mathbf{k}_{t,i}^R], \tag{8}\\ [\mathbf{v}_{t,1}^C; \mathbf{v}_{t,2}^C; \cdots; \mathbf{v}_{t,n_h}^C] = \mathbf{v}_t^C &= W^{UV}\mathbf{c}_t^{KV}, \tag{9}\\ \mathbf{o}_{t,i} &= \sum_{j = 1}^{t} \text{Softmax}_j \left( \frac{\mathbf{q}_{t,i}^T \mathbf{k}_{j,i}}{\sqrt{d_h + d_h^R}} \right) \mathbf{v}_{j,i}^C, \tag{10}\\ \mathbf{u}_t &= W^O [\mathbf{o}_{t,1}; \mathbf{o}_{t,2}; \cdots; \mathbf{o}_{t,n_h}] \tag{11} \end{align*}$$

对于输入$h_t$进行低秩压缩，将$d$维($d=d_h*n_h$, 隐含层维度)输入经过$W^{DKV}\in \mathbb{R}^{d_c\times d}$变换矩阵后得到$\mathbf{c}^{KV}_t$。

$$\begin{align} \mathbf{c}_t^{KV} &= W^{DKV}\mathbf{h}_t, \tag{5}\\ [\mathbf{k}_{t,1}^C; \mathbf{k}_{t,2}^C; \cdots; \mathbf{k}_{t,n_h}^C] = \mathbf{k}_t^C &= W^{UK}\mathbf{c}_t^{KV}, \tag{6}\\ [\mathbf{v}_{t,1}^C; \mathbf{v}_{t,2}^C; \cdots; \mathbf{v}_{t,n_h}^C] = \mathbf{v}_t^C &= W^{UV}\mathbf{c}_t^{KV}, \tag{9} \end{align}$$

然后再通过两个变换矩阵$W^{UK},W^{UV}\in\mathbb{R}^{d\times d_c}$，$\mathbf{c}^{KV}_t$得到$\mathbf{k}_{t}^C,\mathbf{v}_{t}^C$，又将KV的维度扩展回$d$(相当于MHA的每个Head都有单独的K,V)。

DeepSeek-V3: $d=7168,d_c=512$

对比MLA/MHA的KV变换矩阵参数：

两个矩阵$W^{UK},W^{UV}$参数量：$2dd_c=27168512$

正常MHA的参数量是(KV)：$2d\times d =27168*7168$

模型	K/V 生成方式	用了什么参数？	产生的激活值维度（KV Cache）	对比焦点
标准 MHA	每个 token 的输入 $h_t \in \mathbb{R}^d$ 乘上 $W^K, W^V \in \mathbb{R}^{d \times d}$ 得到 K, V	参数量：$2d \times d$	缓存每层、每 token 的 K/V（共 $2 \times L \times d$）	参数量 vs MLA
MLA	先压缩为 $c^{KV}_t \in \mathbb{R}^{d_c}$，再用 $W^{UK}, W^{UV} \in \mathbb{R}^{d \times d_c}$ 展开	参数量：$2d \times d_c$（更少）	最终 K/V 维度仍为 $d$，缓存量并未真正减少	参数量少但缓存未省

Q: 对于MHA的维度？

A：解释:此处主要对比的是变换矩阵的参数量（此矩阵必然被加载进显卡，然后与input进行矩阵运算）

MHA得到QKV的计算公式如下（Linear Layer）：

$$\begin{align*} Q &= XW^Q \\ K &= XW^K \\ V &= XW^V \end{align*}$$

在标准 MHA 中，Query、Key、Value 向量是分别由输入 $X$ 通过线性层 $W^Q, W^K, W^V$ 得到的。虽然这三个矩阵的形状通常都是 $d \times d$，但它们的参数是各自独立的，不共享。KV部分的参数总量就是 $2 \times d \times d$，构成模型参数的一部分。

在看一下Q的优化：

$$\begin{align*} \mathbf{c}_t^Q &= W^{DQ}\mathbf{h}_t, \tag{1}\\ [\mathbf{q}_{t,1}^C; \mathbf{q}_{t,2}^C; \cdots; \mathbf{q}_{t,n_h}^C] = \mathbf{q}_t^C &= W^{UQ}\mathbf{c}_t^Q, \tag{2}\\ [\mathbf{q}_{t,1}^R; \mathbf{q}_{t,2}^R; \cdots; \mathbf{q}_{t,n_h}^R] = \mathbf{q}_t^R &= \text{RoPE}(W^{QR}\mathbf{c}_t^Q), \tag{3} \end{align*}$$

对比MLA/MHA Query部分的参数量：

DeepSeek-V3中$d_q=1536$，$W^{DQ}\in\mathbb{R}^{d_c’\times d},W^{UQ}\in\mathbb{R}^{d_hn_h\times d_c’},W^{QR}\in \mathbb{R}^{d_h^Rn_h\times d_c’}$

MLA: 合计参数量 ≈ 27.5M

• $W^{DQ}$: $d_c’ \times d = 1536 \times 7168 \approx 11M$
• $W^{UQ}$: $d_h n_h \times d_c’ = 7168 \times 1536 \approx 11M$
• $W^{QR}$: $d_h^R n_h \times d_c’ = 3584 \times 1536 \approx 5.5M$（$d_h^R = d_h/2 = 64$, $n_h=56$）

MHA: $d \times d = 7168 \times 7168 \approx 51M$

RoPE位置编码：

$$\begin{align} [\mathbf{q}_{t,1}^R; \mathbf{q}_{t,2}^R; \cdots; \mathbf{q}_{t,n_h}^R] = \mathbf{q}_t^R &= \text{RoPE}(W^{QR}\mathbf{c}_t^Q), \tag{3}\\ \mathbf{k}_t^R &= \text{RoPE}(W^{KR}\mathbf{h}_t), \tag{7}\\ \end{align}$$

$q_t^R,k_t^R\in\mathbb{R}^{d^R_h},d^R_h=\frac 12 d_h=64$

这部分计算的 ktR 实际是个MQA的计算方式，同一层中，所有的Head共享同一个 k

---

🧠 背后推理逻辑：

一、观察 $q_t^R$ 和 $k_t^R$ 的计算方式

我们对比公式 (3) 和公式 (7)：

(3)：

$$\mathbf{q}_t^R = [\mathbf{q}_{t,1}^R; \cdots; \mathbf{q}_{t,n_h}^R] = \text{RoPE}(W^{QR} \mathbf{c}_t^Q)$$

• 输出是一个大向量 $\mathbf{q}t^R$，**明确分成多个 head（$\mathbf{q}{t,i}^R$）**，所以每个 head 都有自己独立的 query。
• 暗示 $W^{QR}$ 的输出维度是 $n_h \cdot d_h^R$。

(7)：

ktR=RoPE(WKRht)\mathbf{k}_t^R = \text{RoPE}(W^{KR} \mathbf{h}_t)

• 注意这里 没有类似的分头结构：没有写成 $[\mathbf{k}{t,1}^R; \cdots; \mathbf{k}{t,n_h}^R]$。
• 它只是一个单一的向量 $\mathbf{k}_t^R$，没有拆成 per-head 的形式。

➡️ 这就是关键区别：query 有多头结构，而 key 没有。

---

二、从维度推出“共享”

你还给出了维度：

$q_t^R, k_t^R \in \mathbb{R}^{d_h^R}$，且 $d_h^R = \frac{1}{2} d_h = 64$

这表示每个 head 的维度是 64，但 $k_t^R$ 只有一个向量。

如果是普通多头注意力：

• 每个 head 应该有自己的 $k_{t,i}^R \in \mathbb{R}^{d_h^R}$。
• 那么就应该有 $n_h$ 个这样的 key 向量，即：$[\mathbf{k}{t,1}^R; \cdots; \mathbf{k}{t,n_h}^R]$

但现在：

• 只有一个 $k_t^R \in \mathbb{R}^{d_h^R}$，那就说明 它没有为每个 head 分配一份，所有 head 共享这一份。

---

三、总结推理链：

1. 公式 (3) 明确拆了多个 head 的 $q$。
2. 公式 (7) 没有拆头，只有一个 $k$ 向量。
3. 维度信息 表明 $k_t^R$ 是一个单向量，而不是 per-head 的矩阵或拼接结构。
4. 所以可以得出推论：这是 MQA 中共享 key 的结构。

因此：