2025-4-10-Transformers without Normalization

Zhu, Jiachen, et al. Transformers without Normalization.

一句话概括：我们使用tanh函数取缔了Transformer中的Normalization Layer。

image-20250410150011602

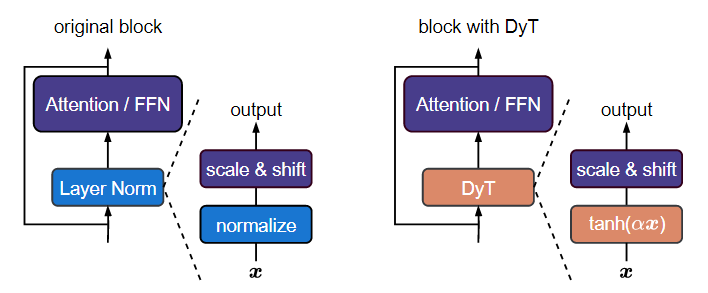
Normalization Layer	Tanh函数
缩放输入激活值	\(\text{DyT}(\alpha x)\),\(\alpha\)是可学习参数、用于调整尺度
压缩极端值	Tanh函数\(\in (0,1)\)，完成压缩极端值

好处：

1. 不需要调整原有架构上超参
2. 提高训练/推理速度

Normalization Layer

对于语言模型，输入是\((B,T,C)\):

• B: Batch数。
• T:Token个数。the number of tokens.
• C: Token Vec向量维度。the number of channels.

\[ \text{normalization}(x)=\gamma *(\frac{\mathbf{x-\mu}}{\sqrt{\sigma^2+\epsilon}})+\beta \]

\(\gamma,\beta\)分别是缩放、平移参数；\(\mu,\sigma^2\)是输入服从分布\(\mathbf{x}\sim N(\mu,\sigma^2)\).

LN的仿射变换？

仿射变换指的就是这个部分： \[ \gamma \cdot \text{normalized\_x} + \beta \] 这一步让模型在对输入进行归一化的基础上，仍然能通过可学习参数\(\gamma\) 和 \(\beta\) 恢复或调整原始特征的尺度和偏移，从而不会因为归一化而限制模型的表示能力。

在标准化（normalization）过程中，目标是对输入数据进行处理，使得它们具有均值为零，方差为一的分布，以此来加速训练过程并提高模型的稳定性。

不同类型的归一化

根据(B,T,C)不同的维度进行归一化：

image-20250410155835785

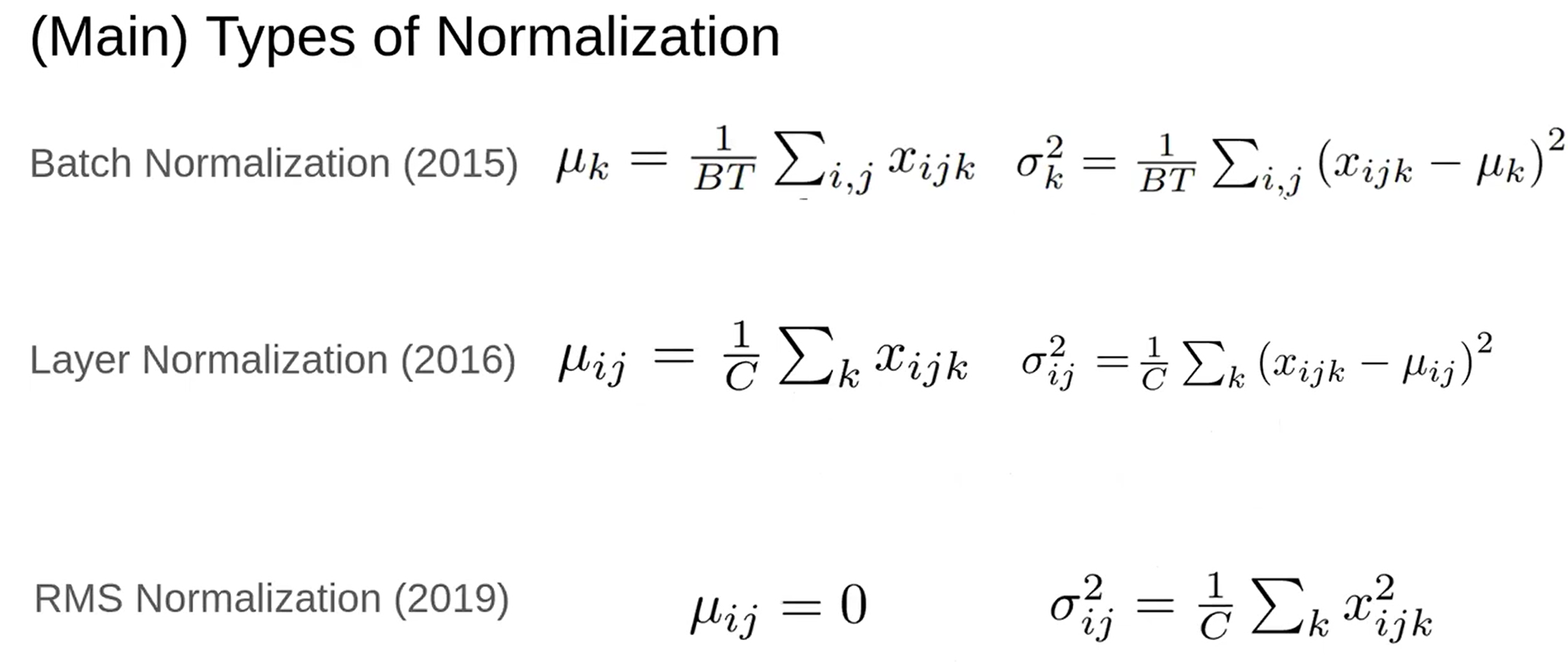
• 批量归一化（BN）：在批量维度上计算均值和方差。虽然BN在卷积神经网络（ConvNet）中使用广泛，但在Transformer模型中应用时存在局限性，因为它需要跨批次和token维度计算统计量。
• 层归一化（LN）：LN独立地对每个token进行归一化计算，计算每个token的均值和方差，因此非常适合Transformer模型。
  • 均方根归一化（RMSNorm）：RMSNorm通过去掉均值中心化步骤，仅使用输入的均方根进行归一化，简化了LN。
  • RMSNorm因其简单和高效，在Transformer模型中逐渐受到欢迎(LLaMA,QWen,DeepSeek,...)。

实验部分：从理论的角度解释

实验1：对不同的transformer架构、在不同的层数、对经过LN前后的输入输出展示：可以看到一开始，在Layer5的时候比较趋向于Linear-Shape，但是往后走，比较偏向于S-Shape。这个曲线与Tanh函数的曲线比较相似。

image-20250410160045586

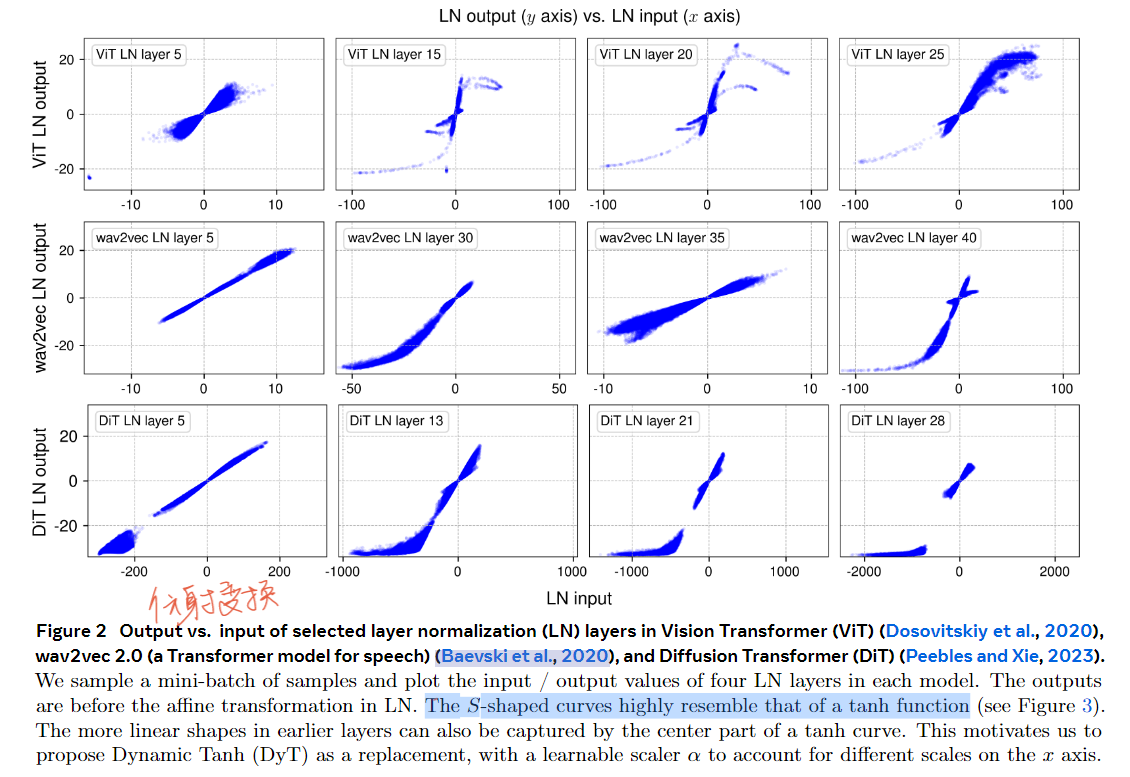
实验2：分别对Token/Channel进行上色。左2图：不同的Tokens上色之后是成直线的、但是所有的Tokens叠加起来是S-Shape；右2图：每个Channel都在不同的区域内是曲线、是Tanh函数(或者说是整条曲线)的部分组成。

image-20250410160717541

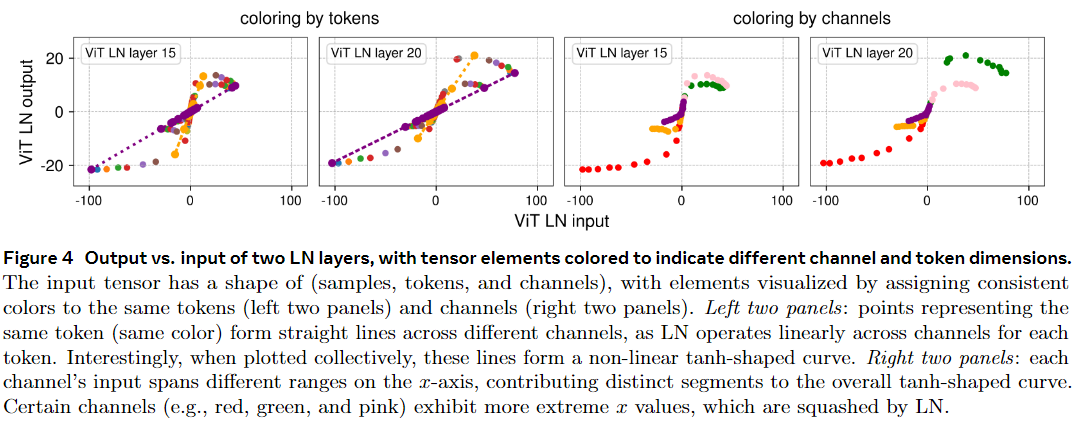
DyT: Dynamic Tangent Hyperbolic

受归一化层与缩放后的双曲正切（tanh）函数形状相似性的启发，此文提出动态双曲正切（DyT）作为归一化层的直接替代品。给定一个输入张量 \(x\)，DyT层定义如下： \[ DyT(x) = \gamma * \tanh(\alpha x) + \beta \quad (2) \] 其中，\(\alpha\) 是一个可学习的标量参数，它能够根据输入范围对输入进行不同的缩放，以处理不同的 \(x\) 尺度（见图2）。这也是我们将整个操作命名为“动态”双曲正切的原因。\(\gamma\) 和 \(\beta\) 是可学习的逐通道向量参数，与所有归一化层中使用的参数相同 —— 它们使输出能够缩放回任意尺度。这有时被视为一个独立的仿射层；出于我们的目的，我们将它们视为DyT层的一部分，就像归一化层也将其包含在内一样。有关DyT在类似PyTorch伪代码中的实现，请参见算法1。

image-20250410161634227

实验：将原始架构中的 LN 或 RMSNorm 替换为 DyT 层

视觉模型

ViT/ConvNeXt-监督学习

我们在 ImageNet-1K 分类任务上训练“Base”和“Large”大小的 Vision Transformer (ViT) (Dosovitskiy et al., 2020) 和 ConvNeXt (Liu et al., 2022) (Deng et al., 2009)。这些模型因其流行和不同的操作而被选中：ViT 中的注意力和 ConvNeXt 中的卷积。

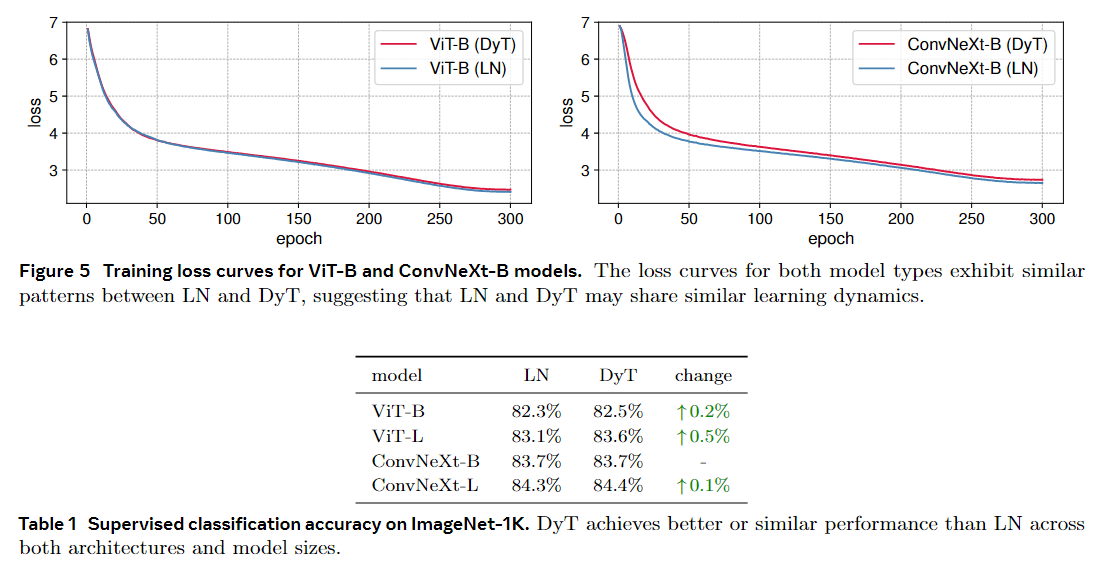
表 1 报告了 top-1 分类精度。DyT 在架构和模型大小上的表现略好于 LN。

图 5 中进一步绘制了 ViT-B 和 ConvNeXt-B 的训练损失。

曲线表明，DyT 和基于 LN 的模型的收敛行为是高度对齐的。

image-20250410161926221

MAE/DINO-半监督学习

我们用两种流行的视觉自监督学习方法进行了基准测试:掩模自编码器(MAE) (He et al.， 2022)和DINO (Caron et al.， 2021)。默认情况下，两者都使用 Vision Transformers 作为主干，但具有不同的训练目标：MAE 使用重建损失进行训练，DINO 使用联合嵌入损失（LeCun，2022）。遵循标准的自监督学习协议，我们首先在 ImageNet-1K 上预训练模型，不使用任何标签，然后通过附加分类层并使用标签对其进行微调来测试预训练模型。微调结果如表2所示。DyT在自监督学习任务中始终与LN相当。

image-20250410163238851

Diffusion Model

我们在 ImageNet-1K 上训练三个大小为 B、L 和 XL 的扩散 Transformer (DiT) 模型（Peebles 和 Xie、2023）（Deng 等人，2009）。补丁大小分别为 4、4 和 2。请注意，在 DiT 中，LN 层的仿射参数用于 DiT 中的类条件，我们将它们保持在我们的 DyT 实验中，仅用 tanh(αx) 函数替换归一化变换。训练后，我们使用标准的 ImageNet“参考批次”评估 Fréchet Inception Distance (FID) 分数，如表 3 所示。 Dyt 比 LN 实现了相当或更好的 FID。

image-20250410163431536

大语言模型

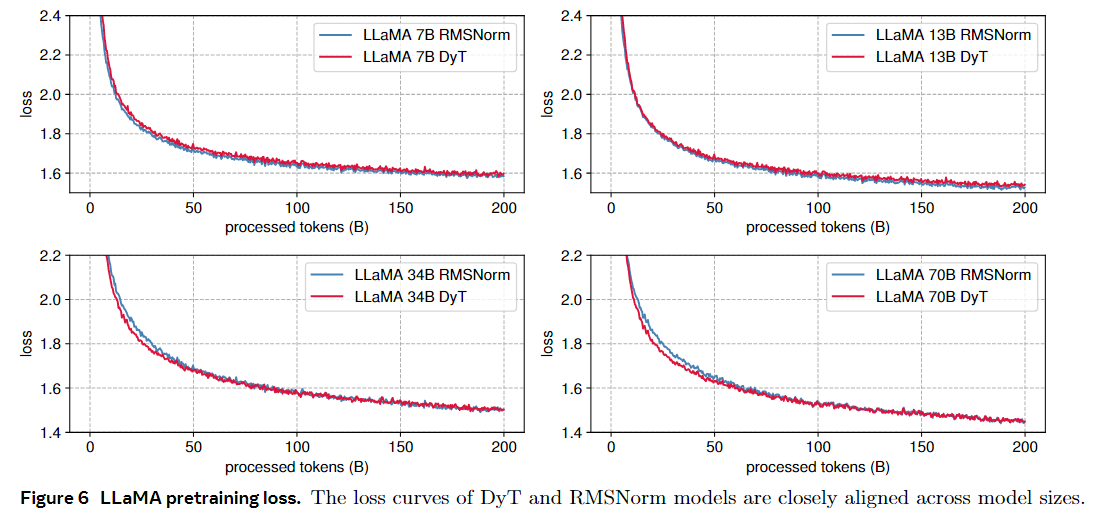
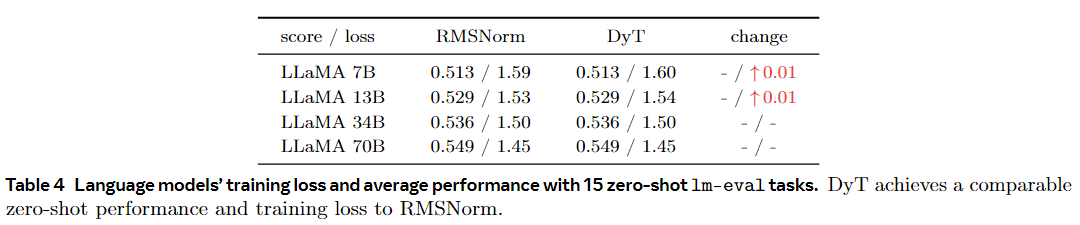
我们预训练 LLAMA 7B、13B、34B 和 70B 模型（Touvron 等人、2023a、b；Dubey 等人、2024），以评估相对于 RMSNorm 的 DyT 性能（Zhang 和 Sennrich，2019 年），LLAMA 中使用的默认归一化层。这些模型是在 Pile 数据集 (Gao et al., 2020) 上训练的，具有 200B 个标记，遵循 LLAMA (Touvron et al., 2023b) 中概述的原始配方。在 DyT 的 LLAMA 上，我们在初始嵌入层之后添加了一个可学习的标量参数，并调整 α 的初始值，如第 7 节所述。我们报告了训练后损失值，并遵循 OpenLLaMA (Geng and Liu, 2023) 对来自 lm-eval 的 15 个零样本任务的模型进行基准测试（Gao et al.）。如表 4 所示，DyT 在所有四种模型大小上的表现与 RMSNorm 相当。图 6 说明了损失曲线，展示了所有模型大小的类似趋势，训练损失在整个训练过程中紧密对齐。

image-20250410163534309

image-20250410163606996

消融实验

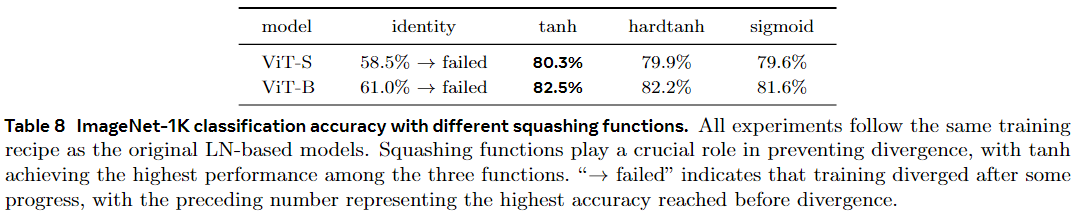
首先评估它们的计算效率，然后是两项研究检查了 tanh 函数和可学习尺度 α 的作用。最后，展示了与以前旨在删除归一化层的方法的比较。

DyT函数的效率

我们使用 RMSNorm 或 DyT 对 LLAMA 7B 模型进行基准测试，通过使用 4096 个标记的单个序列测量 100 次前向传递（推理）和 100 次前向后向传递（训练）所花费的时间。表 7 报告了在 BF16 精度的 Nvidia H100 GPU 上运行时所有 RMSNorm 或 DyT 层以及整个模型所需的时间。与 RMSNorm 层相比，DyT 层显着减少了计算时间，在 FP32 精度下观察到了类似的趋势。DyT可能是面向效率的网络设计的有前途的选择。

image-20250410171128597

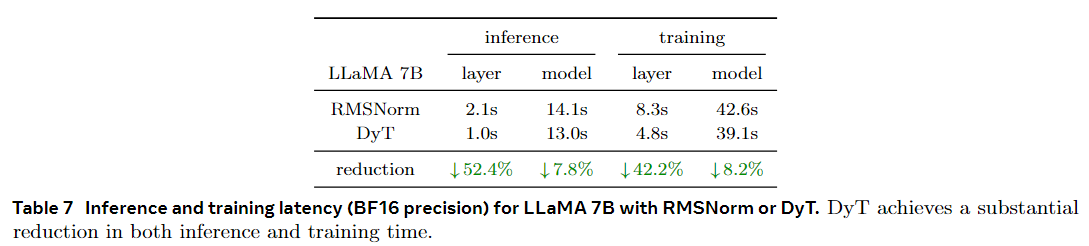
Layer是一层Transformer使用的时间、Model则是整体使用的时间(我猜是一个epoch)

话说，论文中只说了Tanh函数相较于Normalization Layer会降低时间。但是没有对降低时间的理由/原因进行推断呢。也就是只给出了结果，没有给出WHY。

对DyT中Tanh、\(\alpha\)存在的必要性

而进行的消融实验。

image-20250410173013594

image-20250410173021943

image-20250410173050434

\(\alpha\)取值

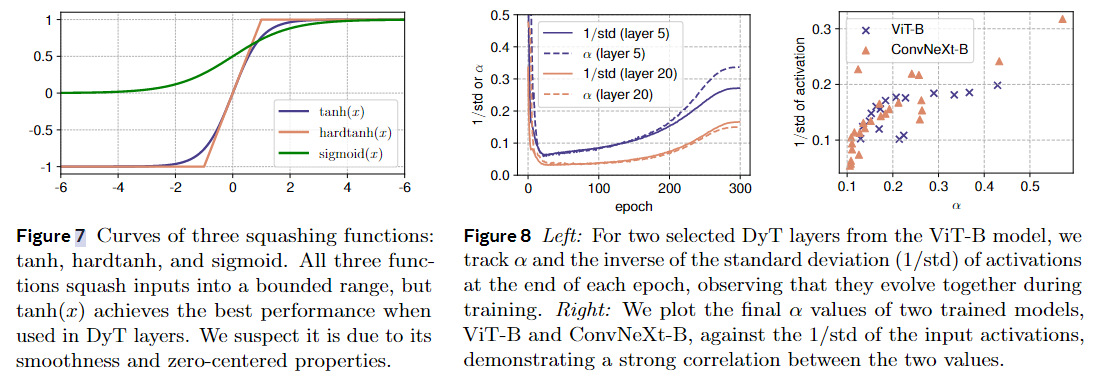
对于图8：左：对于来自 ViT-B 模型的两个选定的 DyT 层，我们跟踪每个 epoch 结束时激活的标准偏差 (1/std) 的倒数，观察到它们在训练期间一起进化。右图：我们根据输入激活的 1/std 绘制了两个训练模型 ViT-B 和 ConvNeXt-B 的最终 α 值，证明了两个值之间的强相关性。

• 在训练期间：我们发现这个 \(\alpha\) 的值会跟着一个叫 “激活的标准偏差的倒数（1/std）” 的东西变。就好比你在游戏里角色的一个能力值（\(\alpha\)），会根据游戏里另一个条件（1/std）变化。从图 8 左边可以看到，一开始 \(\alpha\) 的值会变小，然后又会变大，一直在随着 1/std 的变化而变来变去。这说明 \(\alpha\) 很重要，它能让模型里的数据（激活）保持在一个合适的范围，这样模型就能更好地学习，变得更厉害，训练也能更稳定有效。
• 训练后：等模型训练好了，我们再看这个 \(\alpha\) 的最终值。发现它和 1/std 还有关系呢。如果 1/std 的值大，\(\alpha\) 的值也会大；如果 1/std 的值小，\(\alpha\) 的值也小。而且我们还看到，模型里更深的层次（可以理解成游戏里角色更高级的技能部分），它们的数据变化范围（激活的标准偏差）更大。

最后，\(\alpha\) 这个参数的作用有点像给模型的数据做整理（归一化），但和另一种叫层归一化（LN）的整理方式不一样。LN 是一个一个地整理数据（对每个标记的激活进行归一化），而 \(\alpha\) 是把所有的数据一起整理（对整个输入激活进行归一化）。并且，\(\alpha\) 自己没办法把特别大或者特别小的数据（极值）以一种复杂的方式（非线性方式）变小。(仅 α 不能以非线性方式抑制极值。)

\(\alpha\)初始化

我们发现调整 α（表示为 \(\alpha_0\)）的初始化很少导致显着的性能改进。唯一的例外是 LLM 训练，仔细调整 \(\alpha_0\) 会产生显着的性能提升。在本节中，我们将详细介绍我们的发现对 α 初始化的影响。

非大语言模型

非LLM模型对\(\alpha_0\)相对不敏感。图9显示了不同\(\alpha_0\)对不同任务验证性能的影响。

image-20250410232300835

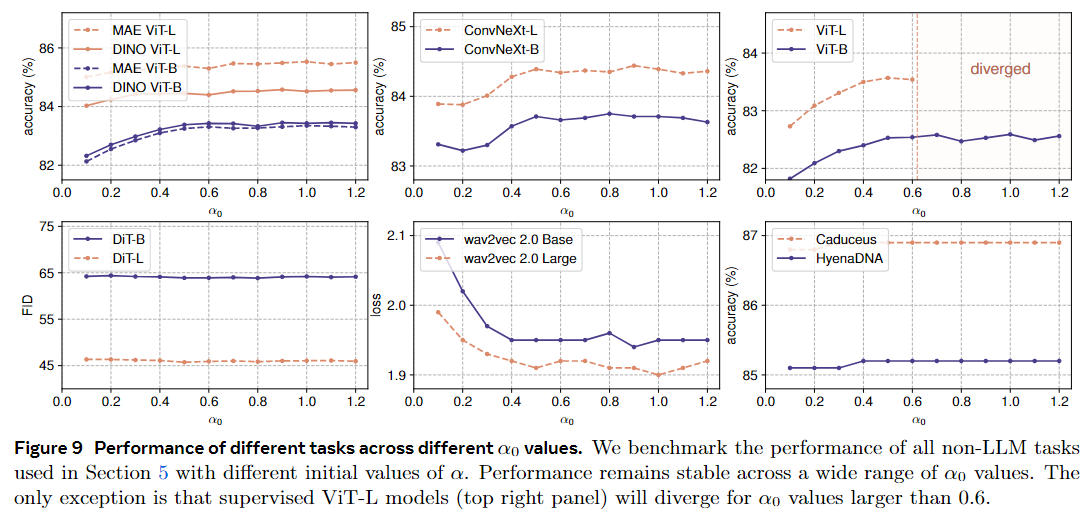
所有实验都遵循各自配方的原始设置和超参数。我们观察到性能在广泛的 \(\alpha_0\) 值范围内保持稳定，值在 0.5 和 1.2 之间通常会产生良好的结果。我们观察到调整 \(\alpha_0\) 通常仅影响训练曲线的早期阶段。主要例外是有监督的 ViT-L 实验，当 \(\alpha_0\) 超过 0.6 时，训练变得不稳定并发散。在这种情况下，降低学习率会恢复稳定性，如下所述。较小的 \(\alpha_0\) 会导致更稳定的训练。基于之前的观察，我们进一步分析了导致训练不稳定的因素。我们的研究结果表明，增加模型大小或学习率需要降低 \(\alpha_0\) 以确保稳定的训练。相反，较高的 \(\alpha_0\) 需要较低的学习率来减轻训练不稳定性。

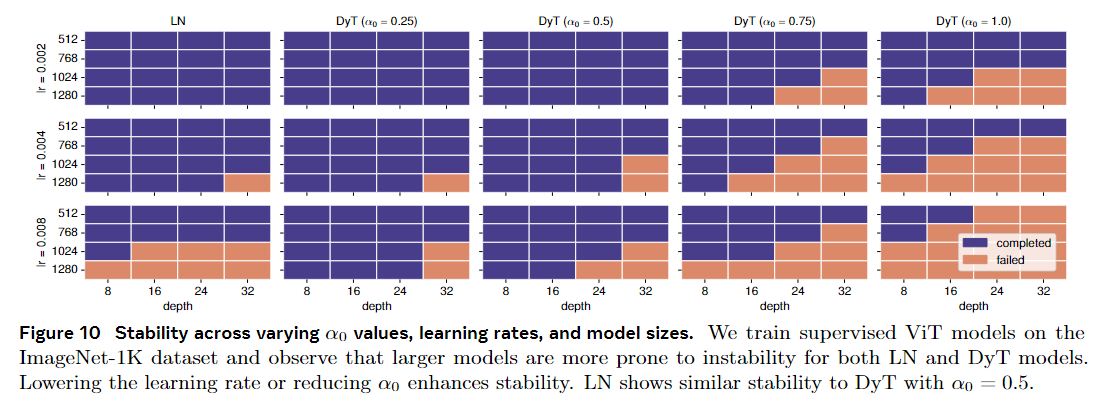
图 10 显示了使用 ImageNet-1K 数据集消融监督 ViT 的训练稳定性。我们改变学习率、模型大小和 \(\alpha_0\) 值。训练更大的模型更容易失败，需要更小的 \(\alpha_0\) 值或学习率来稳定训练。类似的不稳定性模式在可比较的条件下在基于 LN 的模型中也观察到，设置 \(\alpha_0\) = 0.5 会产生类似于 LN 的稳定性模式。

image-20250410232248939

大语言模型

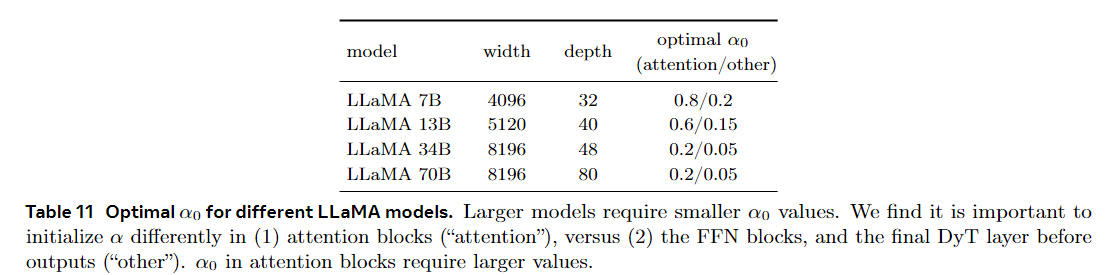
调整\(\alpha_0\)可以提高LLM的性能。如前所述，\(\alpha_0\) = 0.5 的默认设置通常在大多数任务中表现良好。然而，我们发现调整\(\alpha_0\)可以显著提高LLM的性能。我们通过预训练 30B 个标记并比较它们的训练损失来调整 LLAMA 模型的 \(\alpha_0\)。表 11 总结了每个模型的调整后的 \(\alpha_0\) 值。出现了两个关键发现：

1. 较大的模型需要较小的 \(\alpha_0\) 值。一旦为较小的模型确定最佳 \(\alpha_0\)，就可以相应地减小较大模型的搜索空间。
2. 注意块的\(\alpha_0\)值越高，性能越好。

我们发现，在注意块中使用 DyT 层的更高值初始化 α，在其他位置（即，在 FFN 块中或最终线性投影之前）中 DyT 层的较低值可以提高性能。

image-20250410232341407

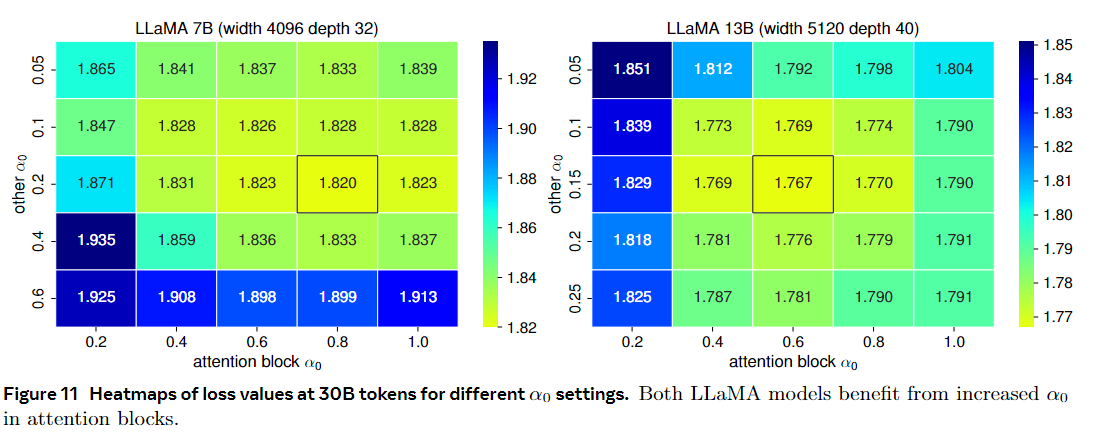
为了进一步说明 \(\alpha_0\) 调整的影响，图 11 显示了两个 LLAMA 模型损失值的热图。两种模型都受益于注意块中更高的 \(\alpha_0\)，导致训练损失减少。

image-20250410232351568

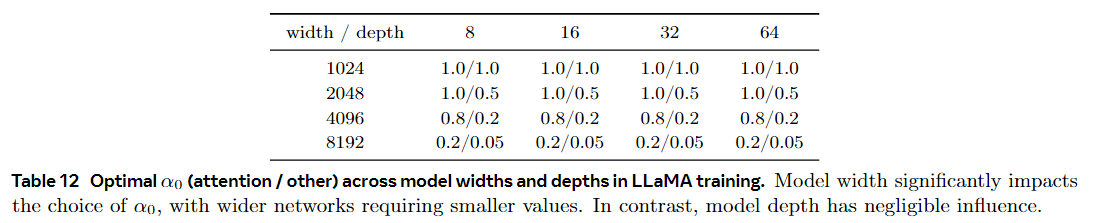
模型宽度主要确定 \(\alpha_0\) 选择。我们还研究了模型宽度和深度对最优\(\alpha_0\)的影响。我们发现模型宽度对于确定最佳\(\alpha_0\)至关重要，而模型深度的影响最小。表 12 显示了不同宽度和深度的最佳 \(\alpha_0\) 值，表明更广泛的网络受益于较小的 \(\alpha_0\) 值以获得最佳性能。另一方面，模型深度对 \(\alpha_0\) 的选择的影响可以忽略不计。

如表 12 所示，网络越宽，“attention”和“other”的初始化越不均匀。我们假设与其他模型相比，LLM α 初始化的灵敏度与其过大的宽度有关。

image-20250410232430752

局限与结论

我们使用 LN 或 RMSNorm 对网络进行实验，因为它们在 Transformer 和其他现代架构中很受欢迎。初步实验（见附录 C）表明 DyT 难以直接在 ResNets 等经典网络中替换 BN。它仍有待更深入地研究 DyT 是否以及如何适应具有其他类型的归一化层的模型。

在这项工作中，我们展示了现代神经网络，特别是 Transformer，可以在没有归一化层的情况下进行训练。这是通过 Dynamic Tanh (DyT) 完成的，这是传统归一化层的简单替换。它通过可学习的比例因子 α 调整输入激活范围，然后通过 S 形 tanh 函数压缩极值。尽管函数更简单，但它有效地捕获了归一化层的行为。在各种设置下，DyT 匹配的模型或超过其归一化对应物的性能。这些发现挑战了对训练现代神经网络中归一化层的必要性的传统理解。我们的研究也有助于理解归一化层的机制，这是深度神经网络中最基本的构建块之一。