3.28：

难绷，一直在补坑。。。

这个补完了：AI Agent介绍

3.29：

这几天一直在看Reinforcement Learning。是的，我的框架还没搭好，原因是看的太浅了，不了解RL的一些执行细节，虽然之前有看过Markov Process，但是又是一段时间过去了，忘的都差不多了。

于是来写RL的一些东西。参考来自于李宏毅的RL介绍。

Reinforcement Learning

一句话介绍：不知道正确的答案，借由与环境互动、根据得到的奖励知道：什么是好的、什么是不好的。

区分ML/RL:

ML：找一个function(映射输入/输出)-->定义loss函数-->最优化

RL：代理或是叫智能体(Agent)与环境(Env)互动(Observation/Action)，相互影响(Reward)

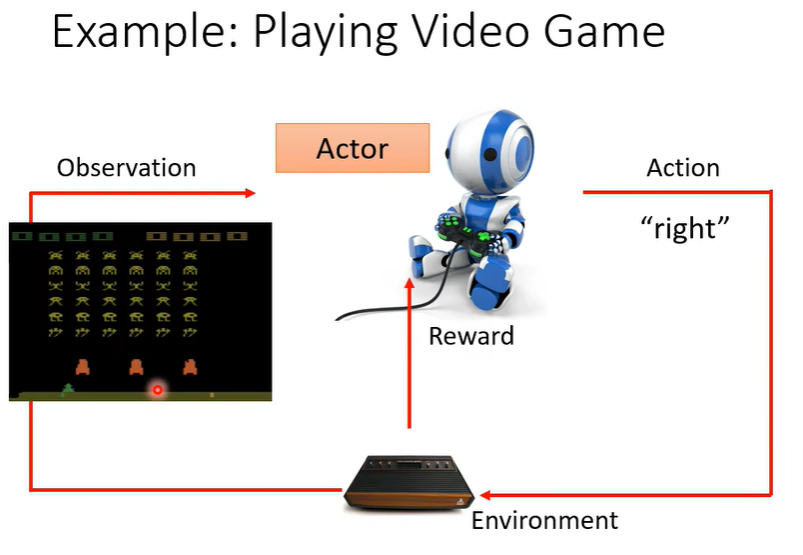
介绍一些术语

Actor/Agent：执行动作的主体，叫做代理或是智能体(下文都称之为智能体)。

Environment：外部的环境。既会影响智能体的行为、又会被智能体执行的行为所影响。

Observation/State：智能体通过环境得到现在的外部的状态、或许还包括了过去对外部状态的观测。

Action：智能体决定执行的动作、会影响到外部的环境。

Policy：智能体A不同于其他智能体B，对于智能体如何决定执行的动作、以及动作又会怎么影响环境(Reward)的整体。可以说是整个模型。通过Reward的optimization可以更新。

Episode：一个episode指的是一句游戏从开始到结束、其中经过的所有的状态以及动作的时间。可以得到一系列\(\{s,a\}\)(状态-动作)的集合。

Trajectory：指一个智能体在环境中进行了一系列动作是所经历的状态、动作、奖励的序列。一般是一个episode可以得到的一系列\(\{s,a\}\)的集合是一个Trajectory。用于训练智能体、学习从状态到动作、最终最大化总体奖励。

Reward：抽象的程度比较高，总的来说就是批判智能体执行当前动作的评价标准。与此相关的概念有：

discount cumculated function: 在状态\(s\)下采取动作\(a\)后，期望获得多少的奖励。
value function：在状态\(s\)下，无论采取什么动作，期望的奖励是多少（对于当前状态的评估，一般是平均期望奖励）。
Advantage function：\(A(s,a)\)表示某个特定动作\(a\)相对于其他动作的优劣程度。

RL与ML之间的联系

对于强化学习来说，实际上比较类似于分类任务，对于给定的输入in:Env-->Observation/State，预测out:Action。并给出不同Action的置信度(然后Agent按照不同Action得到的置信度sample、从Action的distribution中sample)。

要是输入是img，那么和ML也没什么不同。

\[ \text{Action}=f(\text{Observation}) \]

目标: 找到最佳policy(model),\(\max\text{Reward}\)。

对于\(f\)，假如输入是图片、那么需要使用CNN/ViT提取特征；

假如我们想更进一步看到历史的图片，那么可能会选取RNN提取特征。

定义loss

对于RL：经过observation: \(s_1,s_2,\dots,s_T\)(\(T\)时间游戏结束)，在时间\(t\)下施加动作\(a_t\),得到奖励\(r_t\)

计算总奖励: \(R=\sum^T_{t=1}r_t\), 目标(loss func): \(\max R\)

最优化：根据R的值，例如梯度下降更新policy。

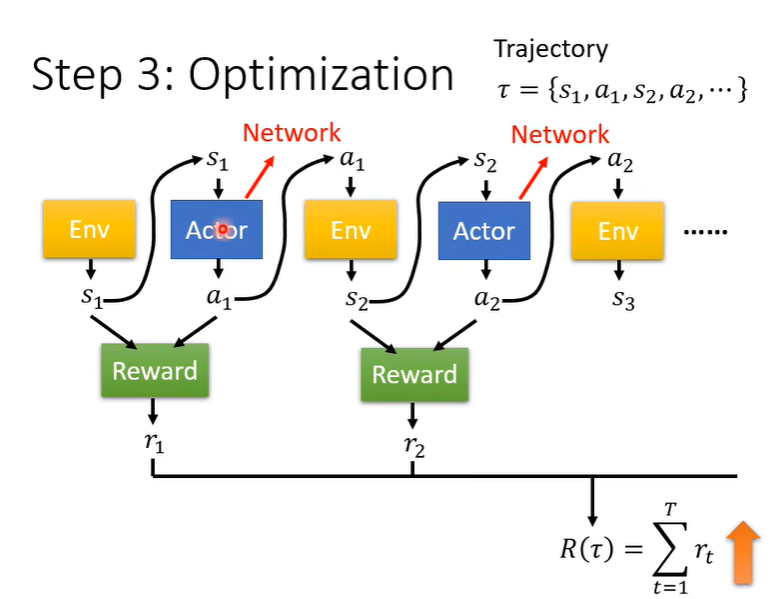
此过程中存在的问题？为什么RL那么难训看人品？

sample具有随机性：动作必须要随机sample，要保证会有没出现过的动作，
Env，Reward，是黑盒(里面是什么不知道)：Env给出对应回应，Reward给出分数，不知道依据什么给出回应。
Env/Reward也具有随机性(随着Action的随机)
重点：如何求解最优化问题？

RL的过程会有点像GAN：

Env: Discriminator

Agent: Generator

如何操控Agent输出

在给定的State下，有两种可能行为：

一定采取行动\(a\)
一定不要采取行动\(a\)

注意：是会采取行动\(a\)，也会采取行动\(b\)；明晰此处的不要采取行动\(a\),说明会采取\(a\)以外动作的可能性。

这是我们能够得到的训练数据（收敛了在不同\(s\)下采取了动作\(a\)/以及不想采取某动作）

Q: 如何收集训练数据？

A: 无论开始状态是什么，我们都跑很多个episodes，记录下对应的、多组\(\{s_1,a_1\},\{s_2,a_2\},\dots,\{s_t,a_t\},\dots\)。

第一阶段：行为克隆（Behavior Cloning）——像监督学习一样训练

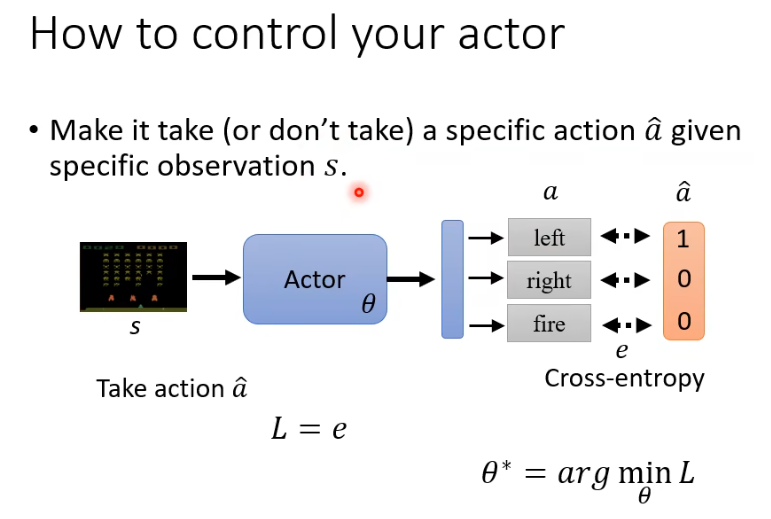
对于Agent，输入State \(s\)，输出Action \(a\)。以此可以收集大量的训练数据: \(\{s_1,\hat a_1\},\{s_2,\hat a_2\},\ldots,\{s_N,\hat a_N\}\)，输出动作与Ground truth之间可以计算交叉熵，这样就有loss，再对loss求梯度下降。

这个过程，我们其实在做的是 模仿学习（Imitation Learning），尤其是其中的 行为克隆（Behavior Cloning）。这时我们有 expert 给的 “正确动作” \(\hat{a}\)，可以直接用交叉熵 loss： \[ \mathcal{L}_{\text{BC}} = -\log \pi_{\theta}(\hat{a} | s) \] ✅ 这是纯监督学习：用 expert 数据模仿他该怎么做，不涉及任何 reward、Q value、优势函数之类的强化学习概念。

第二阶段：从模仿走向强化学习

但问题是 —— 行为克隆有局限性：

如果 expert 数据少、分布不够全，Agent 在训练中可能从没见过某些 state，就不知道该如何决策。

没法根据环境反馈进一步“变得更强”，只能学 expert 的行为，无法超越。

于是，我们从“模仿”走向“试错 + 奖励驱动”的强化学习。这时：

没有 ground truth 动作了（只有 Agent 自己选择的 a）
我们只知道这个动作带来了多少 reward
所以，我们要优化的，不是“像 expert 一样”，而是“动作好就多选它，动作差就少选它”

这时候就引入了策略梯度： \[ \mathcal{L}_{\text{PG}} = - \log \pi_{\theta}(a | s) \cdot R \] 进一步为了减小方差，引入了优势函数： \[ \mathcal{L}_{\text{PG}} = - \log \pi_{\theta}(a | s) \cdot A(s,a) \]

阶段	方式	数据来源	优化目标	是否需要 Advantage
模仿学习	行为克隆（交叉熵）	expert 提供的 \(\hat{a}\)	拟合 expert 的行为	❌ 不需要
强化学习	策略梯度（REINFORCE）	Agent 自己采样的 \(a\)	最大化 reward	✅ 需要

这种从行为克隆（交叉熵）到策略梯度（交叉熵 + Advantage 权重）的逻辑演化，是许多强化学习算法的实际路径。例如：

初期 warm-up 用行为克隆
后期切到策略梯度微调，用 Advantage 来权衡每个动作的好坏

优势函数的提出

Agent对于不同的动作会有不同程度的偏向，我们要显化这种偏向，使用优势函数。

优势函数：期望在\(s_1\)下做动作\(\hat a_1\)，在\(s_2\)下不做动作\(\hat a_2\)，期望的程度是不同的。 \[ A(s,a)=Q(s,a)-V(s) \]

\(A(s,a)\): Advantage Function。表示某个特定动作\(a\)相对于其他动作的优劣程度。
\(Q(s,a)\): Discounted Cumulative Reward。在状态\(s\)下采取动作\(a\)后，期望获得多少奖励。
\(V(s)\): Value Function。在状态\(s\)下，无论采取什么动作，期望的奖励是多少。（当前状态的期望reward）

\[ A(s,a)=\begin{cases} >0,&动作a在状态s下比平均水平好\\ <0,&动作a在状态s下比平均水平差 \end{cases} \]

2025-3-28/29-RL简介