2025-5-15

背景

现有目标检测方法在理想场景下表现优异

复杂菜品混合场景是“真实世界”的挑战（遮挡、混合、模糊）

提出 RL-DETR，增强 query 演化能力，泛化到复杂场景

目前与食品有关的目标检测数据集都是不同的菜品之间本身分割的比较开，因此预测bbox并不困难，而且因为不同的菜品放在不同的碗里，导致识别bbox的准确度非常高，导致对一张图片中的菜品进行检测就近似于图像分类任务，因此这样进行目标检测的准确度十分的高。

但实际在中餐之间，我们常会将不同的菜品夹到同一个餐盘之中。这样会导致不同菜品之间会存在混合、覆盖等情况，极大地增大了目标检测的难度。但目前的研究多集中在西餐、以及中菜小碗菜上，这些类别下的菜品并不粘连、大小相似、几近于理想的目标检测环境。对于研究混合菜品的研究几乎没有。

但是对此研究的话，有如下的好处：1.填补了在中菜不同菜品混合研究中空白；2.便于落地，赋能对于入口食物的成分管理；3.有助于响应国家提出的”健康战略”，帮助人们追求健康。（由细至粗，由小及大）

2025年3月9日，国家卫生健康委员会主任雷海潮在十四届全国人大三次会议记者会上宣布，将持续推进“体重管理年”3年行动，直面我国超重肥胖率持续攀升的严峻挑战。数据显示，我国成人超重肥胖率已达50.7%，青少年肥胖率15年增长12倍，每年因肥胖导致的直接医疗费用超2400亿元。更令人担忧的是，研究预测若不干预，2030年成人超重肥胖率将达70.5%，儿童肥胖率将达31.8%。

方法

针对一个餐盘中不同菜品之间存在混合、覆盖的情况，对不同菜品进行目标检测。本工作针对复杂场景下的菜品检测任务，提出一种基于Reinforcement Learning的Transformer目标检测方法。该方法将DETR结构中的查询更新过程建模为序列决策问题，引入高斯策略与奖励函数，通过RL框架优化解码器更新策略，提升模型在菜品混合、遮挡、边界模糊等复杂场景中的检测能力。

目标：借助大量“清晰边界”数据与少量“混合遮挡”数据，提升在复杂遮挡场景下的目标检测性能。小样本复杂场景泛化是从“理想检测分布”泛化到“复杂检测分布”的问题: 首先找到中菜的粗略数据分布的地方、然后依靠复杂的混合菜品图片，对数据分布进行更细致地定位。

不改变整体类别空间（例如仍然是中餐、常见菜品）

但显著增加目标检测任务的感知难度：如遮挡、密集、小目标、模糊边界

而混合菜图片少，构成小样本

目标检测模型需具备一定跨场景适应能力：跨域vs跨场景

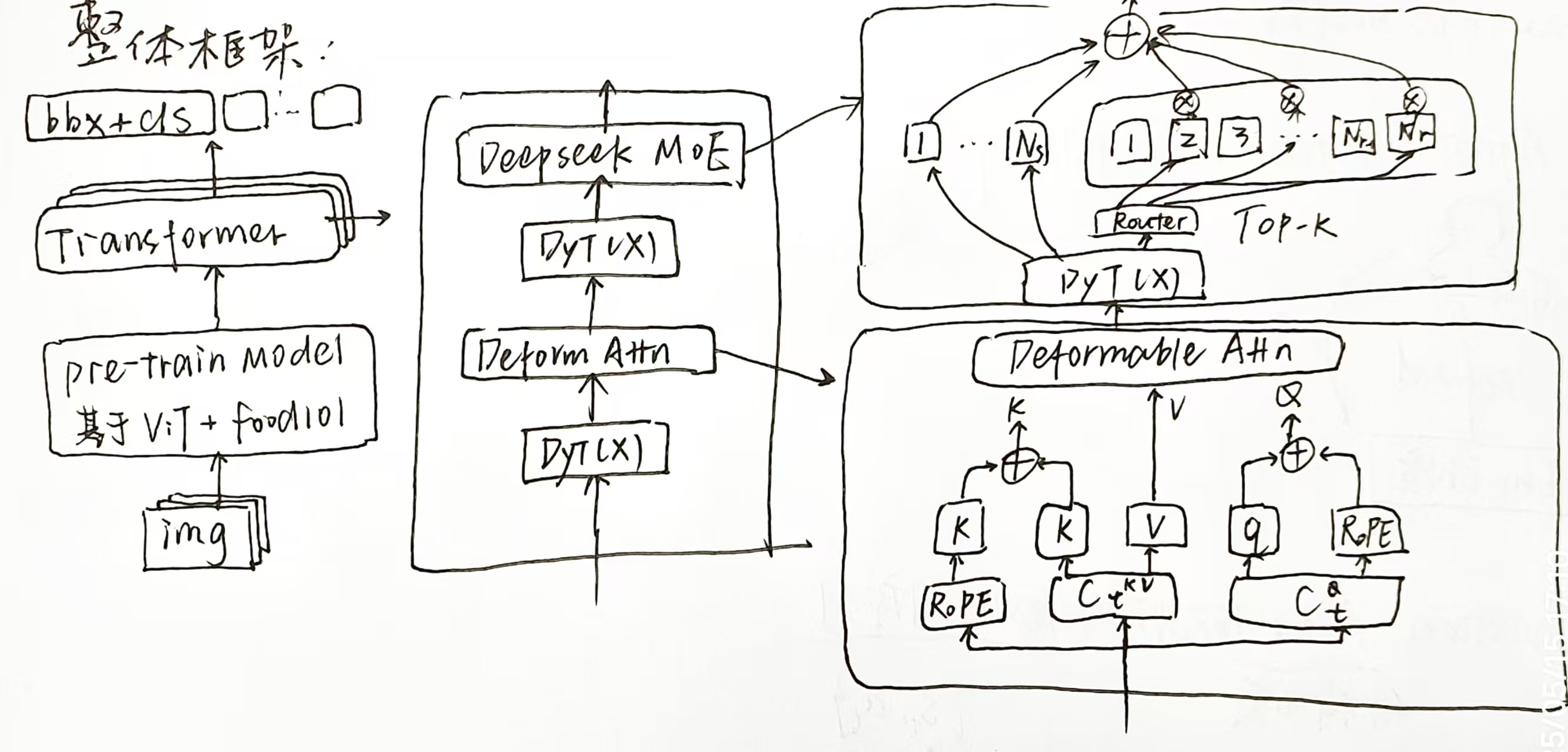
整体框架

此处对整体框架进行一定陈述。整个模型由以下三部分组成：

图像编码模块：输入图像通过预训练的ViT模型提取图像特征，输出 $x \in \mathbb{R}^{H \times W \times d}$，其中 $d$ 为特征维度。
Transformer编码器-解码器结构：包括6层标准编码器和6层解码器，编码器提取全局语义信息，解码器迭代更新对象查询，最终输出边界框和类别。
RL增强查询更新机制：解码器每层对查询的更新通过高斯采样实现，动作具有随机性；每一层的中间预测均计算奖励以用于强化学习训练。

$H, W$：输入图像的高和宽（比如 224）
$C$：图像通道数，通常为 3
$d$：特征维度（例如 ViT 的 hidden dim，通常为 256 / 512 / 768）
$N$：object query 数量（如 100）
$B$：batch size
$L$：解码器层数（如 6）

模型各模块输入输出维度hybr

模块	输入维度	输出维度	说明
ViT 图像编码器	$(B, C, H, W)$	$(B, T, d)$	T 是 patch 数量，例如 $\frac{H \times W}{P^2}$，P 为 patch size
Encoder（×6 层）	$(B, T, d)$	$(B, T, d)$	输出为图像特征编码
初始查询 $q_0$	learnable 参数	$(B, N, d)$	作为第 0 层 query
Decoder第 k 层输入 $q_k$	$(B, N, d)$ + encoder输出 $(B, T, d)$	$h_k \in (B, N, d)$	经过 self/cross attention 和 FFN
均值和方差生成	$h_k \in (B, N, d)$	$\mu_k, \log \sigma_k^2 \in (B, N, d)$	两个 linear 层生成
高斯采样 query	$\mu_k, \sigma_k \in (B, N, d)$	$q_{k+1} \in (B, N, d)$	用于下一层 decoder
Decoder最终输出 $q_L$	$(B, N, d)$	用于后续预测
分类头	$(B, N, d)$	$(B, N, C_{\text{cls}})$	linear 映射到类别数
回归头（边界框）	$(B, N, d)$	$(B, N, 4)$	映射为中心坐标 + 宽高
value网络（可选）	$(B, N, d) \rightarrow (B, d)$（池化）	$(B, 1)$	输出状态值 $V(q_k)$
动作概率 $( \pi_\theta(o \vert q) )$	$\mu_k, \sigma_k, q_{k+1} \in (B, N, d)$	$(B,)$	多维高斯概率密度或 log prob

所有的 query 和特征均为 shape $(B, N, d)$，适合 transformer 操作；

多个 decoder 层共享 encoder 输出，但 query 是逐层更新；

分类输出是对每个 query 预测一个目标；

回归头输出每个 query 对应一个边界框（通常是 $[x_c, y_c, w, h]$ 格式）；

Value 网络对 query 向量聚合后预测状态值，可用于计算 Advantage；

动作的概率 $\pi_\theta(o|q)$ 是高斯分布中采样点的 log prob 或 density，用于计算 PPO 中的策略比值。

基于RL的Loss函数设计

状态定义

在第 $k$ 层解码器中，状态定义为该层的对象查询：

$s_k = q_k \in \mathbb{R}^{N \times d},$

其中 $N$ 是对象查询的数量，$d$ 是特征维度，$q_k$ 表示第 $k$ 层解码器的查询输入，是从 $q_{k-1}$ 经过处理后得到的。

动作定义

动作是对当前查询 $q_k$ 的更新过程，即：

$a_k: q_k \longrightarrow q_{k+1},$

不同于传统DETR中确定性更新，我们引入高斯策略，将动作表示为一个从高斯分布中采样的随机变量：

$q_{k+1} \sim \mathcal{N}(\mu_k, \Sigma_k),$

其中

$\mu_k = W_{\mu} h_k, \quad \log \sigma_k^2 = W_{\sigma} h_k,$

$h_k \in \mathbb{R}^{N \times d}$ 是通过标准解码器结构（包括自注意力、交叉注意力和前馈网络）对查询进行处理后的中间特征表示：

$h_k = \text{FFN}(\text{CrossAttn}(\text{SelfAttn}(q_k), x)).$

从而每个位置的下一步查询由如下方式采样：

$q_{k+1} = \mu_k + \epsilon_k \cdot \sigma_k, \quad \epsilon_k \sim \mathcal{N}(0, I).$

这种方式引入了动作的概率建模，支持策略梯度优化。

奖励设计

每一层输出的对象查询 $q_{k+1}$ 会生成边界框和类别预测，通过以下方式与真实标签比较并计算奖励：

使用 Hungarian 匹配算法匹配预测与真实目标；
计算预测框与真实框的平均 IoU：$\text{mean}(\text{IoU}_k)$；
计算分类准确率 $\text{accuracy}_k$。

奖励 $r_k^i$：定义为 当前层的检测损失的负数，即

$r_k^i = -\left(\mathcal{L}_{\text{cls}}^i + \lambda \cdot \mathcal{L}_{\text{box}}^i\right)$

其中损失根据该层 decoder 输出的 object query 所产生的预测（bbox+class）与 GT 匹配计算。

$\mathcal{L}^{\text{cls}}_i$：分类损失（分类正确性）
$\mathcal{L}^{\text{box}}_i$：边界框回归损失（位置精度）

对于第 $i$ 层 decoder 输出的查询 $q_i$，你会通过 detection head 得到每个查询预测的类别概率分布：

$p_i^{(j)} = \text{Softmax}(W_{\text{cls}} q_i^{(j)})$

其中：

$j = 1, 2, …, N$，表示每个 object query；
$W_{\text{cls}}$ 是线性分类头参数。

使用 Hungarian Matching 算法将每个预测与 GT 匹配，得到匹配对 $(j, t_j)$，其中 $t_j$ 是对应的真实类别。然后分类损失为：

$\mathcal{L}^{\text{cls}}_i = \frac{1}{N} \sum_{j=1}^{N} \text{CE}(p_i^{(j)}, t_j)$

可引入 no-object 类别（background 类别），以处理未匹配查询。

同样地，每个查询 $q_i^{(j)}$ 会预测一个边界框：

$\hat{b}_i^{(j)} = \text{MLP}_{\text{box}}(q_i^{(j)}) \in [0,1]^4$

表示归一化后的 $(cx, cy, w, h)$ 或者 $(x_1, y_1, x_2, y_2)$。

对每一对匹配好的 GT 边界框 $b_j^\star$，计算损失：

$\mathcal{L}^{\text{box}}_i = \frac{1}{N} \sum_{j=1}^{N} \left( \|\hat{b}_i^{(j)} - b_j^\star\|_1 + \gamma \cdot (1 - \text{GIoU}(\hat{b}_i^{(j)}, b_j^\star)) \right)$

其中：

第一项是 L1 loss；
第二项是广义IoU损失；
$\gamma$ 是控制两者权重的超参数，通常设为 2.0；
框匹配同样基于 Hungarian algorithm。

价值函数 $V(q_k^i)$

可以用一个 MLP 头对每个 $q_k^i$（或者 mean pooled query）输出一个标量：

$V(q_k^i) = \text{MLP}_{\text{value}}(q_k^i)$

建议使用均值池化所有 query 后输入 value 网络：

$\bar{q}_k = \frac{1}{N} \sum_{j=1}^N q_k^{(j)}, \quad V(q_k) = \text{MLP}(\bar{q}_k)$

优势函数 $A_k^i$

用标准 TD 一步法：

$A_k^i = r_k^i + \gamma V(q_{k+1}^i) - V(q_k^i)$

也可以用 GAE（Generalized Advantage Estimation）进行平滑。

强化学习优化目标

为了稳定更新对象查询策略，我们引入 GPRO（Generalized PPO with Reference Policy）作为优化目标。在本模型中，强化学习中的动作为 更新对象查询向量 $q_k$，我们通过建模其分布 $\pi_\theta(o_k|q_k)$ 实现对动作的采样与优化。完整目标函数如下：

$\mathcal{J}_{\text{GPRO}}(\theta) = \mathbb{E}_{q_k, o_k \sim \pi_{\theta_{\text{old}}}} \left[ \frac{1}{G} \sum_{i=1}^{G} \left( \min\left( \frac{\pi_\theta(o_k^i|q_k^i)}{\pi_{\theta_{\text{old}}}(o_k^i|q_k^i)} A_k^i,\, \text{clip}\left(\frac{\pi_\theta(o_k^i|q_k^i)}{\pi_{\theta_{\text{old}}}(o_k^i|q_k^i)}, 1 - \epsilon, 1 + \epsilon \right) A_k^i \right) - \beta \, \mathbb{D}_{\text{KL}}\left(\pi_\theta(\cdot|q_k^i) \| \pi_{\text{ref}}(\cdot|q_k^i)\right) \right) \right]$

当前策略 $\pi_\theta(o_k|q_k)$

每一层 decoder 输出：

$\mu_k = W_\mu h_k$，
$\log \sigma_k^2 = W_\sigma h_k$

动作为：

$o_k = q_{k+1} = \mu_k + \epsilon \cdot \sigma_k, \quad \epsilon \sim \mathcal{N}(0, I)$

所以：

$\pi_\theta(o_k|q_k) = \mathcal{N}(o_k;\, \mu_k, \sigma_k^2)$

这是多维高斯分布（注意是独立维度），其对数概率为：

$\log \pi_\theta(o_k|q_k) = -\frac{1}{2} \sum_j \left[ \frac{(o_k^j - \mu_k^j)^2}{\sigma_k^{j\,2}} + \log \sigma_k^{j\,2} \right] + \text{const}$

用这个公式计算当前策略和旧策略的比值：

$r_k^i = \exp\left( \log \pi_\theta(o_k^i|q_k^i) - \log \pi_{\theta_{\text{old}}}(o_k^i|q_k^i) \right)$

KL 散度项 $\mathbb{D}_{\text{KL}}(\pi_\theta | \pi_{\text{ref}})$

$\pi_{\text{ref}}$ 是参考策略，这里你可以选择：

Deterministic decoder：比如标准DETR中确定性更新的 query，即：
$q_{k+1}^{\text{ref}} = \mu_k$
所以参考策略为 delta 分布。

此时，KL 散度简化为「当前策略对 deterministic query 的 KL」，等价于：

$\mathbb{D}_{\text{KL}}(\pi_\theta(\cdot|q_k^i) \| \delta(q_{k+1}^{\text{ref}})) = -H(\pi_\theta) \text{（最大似然形式）}$

更常见做法是用 $\pi_{\theta_{\text{old}}}$ 作为参考，即 PPO 中标准做法。

模型训练

训练前期，冻结 ViT 和 encoder，仅训练 decoder 查询更新模块（动作生成器），先训练强化学习部分。
每一层 decoder 都输出 query 的分布参数 $(\mu_k, \sigma_k)$，采样新 query。
根据每层 query 输出的分类框 + 边界框，计算检测损失，转为 reward。
用采样路径和 reward 计算优势 $A_i$，计算 GPRO loss 进行反向传播。

模型更新

为了将 GPRO 强化学习目标用于你的 Transformer 检测框架，并实现模型更新，以下内容将从采样动作、计算损失、反向传播优化三个层面，详细讲解你的模型如何训练更新。

第 1 步：前向传播（采样动作）

对于每一张图像，每层解码器执行以下操作：

当前对象查询为 $q_k \in \mathbb{R}^{N \times d}$
计算均值与方差：
$\mu_k = W_\mu h_k,\quad \log \sigma_k^2 = W_\sigma h_k$
从高斯分布采样新的 query 作为动作（即下一层 query）：
$q_{k+1} = \mu_k + \epsilon_k \cdot \sigma_k, \quad \epsilon_k \sim \mathcal{N}(0, I)$
每层 $q_k$ 都被送入 decoder 得到边界框和类别预测，用于后续 reward 计算。

第 2 步：构建强化学习目标（GPRO）

计算动作概率比（策略比值）

假设每个动作 $o_i = q_{k+1}^i$，其分布为多维独立高斯：

$\pi_\theta(o_i|q_k) = \mathcal{N}(o_i; \mu_k, \sigma_k^2)$

使用标准高斯公式，逐维计算 log 概率，然后指数差值得到策略比值：

$r_i = \frac{\pi_\theta(o_i|q_k)}{\pi_{\theta_{\text{old}}}(o_i|q_k)} = \exp\left( \log \pi_\theta(o_i|q_k) - \log \pi_{\theta_{\text{old}}}(o_i|q_k) \right)$

注意：$\pi_{\theta_{\text{old}}}$ 表示动作采样时使用的旧参数，因此在训练中需要缓存在 buffer 中。

计算奖励 $r_k^i$

使用每层 decoder 输出的预测结果（边界框 + 类别）与 ground truth 计算检测损失（Hungarian 匹配后）：

$r_k^i = -\left( \mathcal{L}_{\text{cls}}^i + \lambda \cdot \mathcal{L}_{\text{box}}^i \right)$

其中：

$\mathcal{L}_{\text{cls}}^i$：交叉熵或 focal loss；
$\mathcal{L}_{\text{box}}^i$：GIoU Loss + L1 Loss

计算优势函数 $A_k^i$

使用 TD 一步法或 GAE：

$A_k^i = r_k^i + \gamma V(q_{k+1}^i) - V(q_k^i)$

其中 $V(\cdot)$ 是 value 网络，可由 MLP 对 query 向量池化后计算。

计算 GPRO loss

对每个样本，计算：

$L_{\text{GPRO}} = \frac{1}{G} \sum_{i=1}^G \left[ \min\left(r_i \cdot A_i,\, \text{clip}(r_i, 1 - \epsilon, 1 + \epsilon) \cdot A_i \right) - \beta \cdot \mathbb{D}_{\text{KL}}(\pi_\theta \| \pi_{\text{ref}}) \right]$

第 3 步：反向传播与更新

使用 PyTorch 的标准反向传播机制：

1
2
3

optimizer.zero_grad()
loss.backward()
optimizer.step()

需要优化的参数：

所有用于生成 $\mu_k, \sigma_k$ 的 decoder 层；
用于 bbox/class 预测的输出头；
可选：value 网络参数（用于估计 $V(q_k)$）；
可选：encoder/backbone 若不冻结。

Tips：模型更新中的关键实践建议

环节建议

buffer 保存旧策略参数 $\theta_{\text{old}}$，每 K 次迭代更新一次

baseline 使用 value 网络减小优势估计的方差

KL项策略初期可关闭 $\mathbb{D}_{KL}$，后期加入以稳定训练

采样策略可用多个采样重复 query 更新，提升训练稳定性

损失总和将 detection loss + GPRO loss 合并训练（两阶段 or 混合）

环节	建议
buffer	保存旧策略参数 $\theta_{\text{old}}$，每 K 次迭代更新一次
baseline	使用 value 网络减小优势估计的方差
KL项策略	初期可关闭 $\mathbb{D}_{KL}$，后期加入以稳定训练
采样策略	可用多个采样重复 query 更新，提升训练稳定性
损失总和	将 detection loss + GPRO loss 合并训练（两阶段 or 混合）

4. 实验（Experiments）

FoodDet100k上预训练
MixFood500上微调评估 / 零样本评估
与DETR、Deformable DETR、DINO对比
分析遮挡目标上的表现变化

5. 消融实验

没有RL奖励 vs 使用RL奖励
使用复杂目标加权 vs 未加权
GPRO vs PPO / REINFORCE