2025-3-13-模型构建

Zheng, Minghang, et al. "End-to-end object detection with adaptive clustering transformer." arXiv preprint arXiv:2011.09315 (2020).

感觉这个图的形式差不多是我想画的样子。

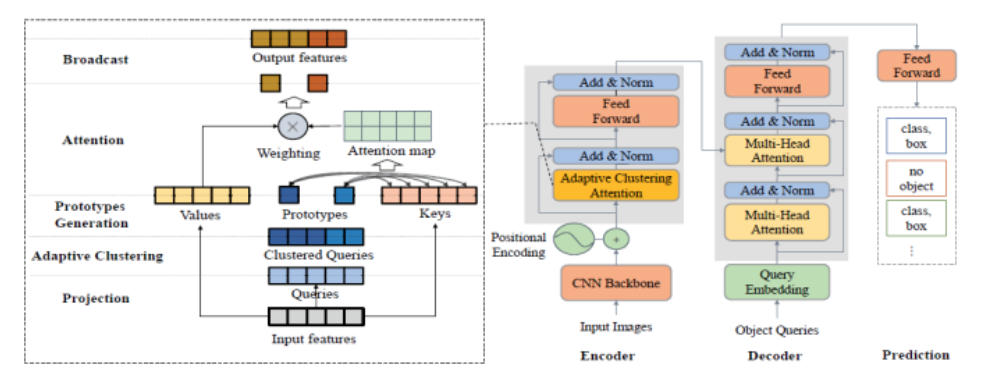
然后来写我的模型——可恶就是不想写

首先，我不打算使用知识蒸馏。或许后续可以使用训练好的模型再进行知识蒸馏。

输入是一系列的图片，然后将其划分为16*16的patch，然后+pos encoding

得到一系列的向量

投入transformer（DS修改版）*N

输出pred head

对于每层decoder输出的pred head,作为序列信息，用于强化学习。

将 DETR 的解码器每层视为 RL 的一步，定义状态为当前层的对象查询，动作为更新查询，奖励为当前预测与真实框的 IoU（交并比）或分类准确度。

State	Action	Reward
状态定义为当前层的对象查询。	动作是更新这些查询。	奖励基于预测与真实框的 IoU 或分类准确度。
每一层的状态是当前的对象查询，这些查询用于预测边界框和类别。	动作是解码器层对对象查询的更新。为了让 RL 工作，需要让更新有随机性，比如在更新时加入噪声。	奖励函数可定义为均值 IoU 加权分类准确度。

这种方法类似于添加辅助损失，可能与标准训练效果类似，但 RL 可提供更多探索性。

梯度更新：

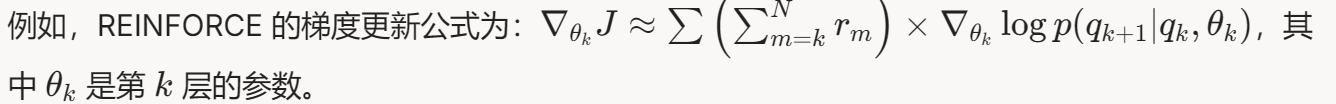
状态定义

状态$s_k $ 定义为第 $ k$ 层输入的对象查询$q_k $。这些查询是解码器从上一层继承的，用于与编码器输出交互，生成预测。
在 RL 框架中，状态反映当前环境，对象查询的当前状态直接影响后续层的预测。

动作定义

动作 $a_k $是第$ k $层对对象查询的更新，即从$q_k $到$ q_{k+1}$ 的变换。在标准 DETR 中，这一更新是确定性的，由自注意力、交叉注意力和前馈网络决定。
为使 RL 工作，需引入随机性，使更新成为概率分布。例如，可以让层输出对象查询的均值和方差，从正态分布中采样$q_{k+1} $，概率为$p(q_{k+1} | q_k, _k) $，其中$_k $ 是层的参数。

奖励定义

奖励 $r_k $基于第$ k$ 层输出 $q_{k+1} $后的预测质量。预测包括边界框和类别标签，与真实框比较。
计算方法：
1. 用 $q_{k+1}$ 生成预测边界框和类别。
2. 用匈牙利算法匹配预测与真实框，计算均值IoU$\text{mean}(\text{IoU}_k)$和分类准确度（$\text{accuracy}_k$）。
3. 奖励公式为：$ r_k = (_k) + _k $，其中$$是权重因子，需实验确定（如 0.5）。
替代方案：奖励可以是负损失，即$r_k = - (\text{box\_loss}_k + \text{class\_loss}_k)$ ，其中 $\text{box\_loss}_k$ 和$\text{class\_loss}_k$ 是基于当前预测的边界框回归损失和分类损失。

优化过程

目标是最大化所有层的累积奖励：$ J = $ 。
使用 RL 算法如 REINFORCE，梯度更新公式为： $\nabla_{\theta_k} J \approx \sum \left( \sum_{m=k}^N r_m \right) \times \nabla_{\theta_k} \log p(q_{k+1} | q_k, \theta_k)$ 其中，内层和是所有样本，外层和是从第 k k k 层到最后层的奖励总和，反映每一层的贡献。
实际中，可用策略梯度方法（如 PPO）优化，考虑探索性和稳定性。

实际应用示例

假设 DETR 解码器有 6 层（N=6 N = 6 N=6），训练过程如下：

初始化对象查询，输入第一层。
每层输出更新后的对象查询，立即用当前查询预测边界框和类别。
计算当前预测的均值 IoU 和分类准确度，代入公式$ r_k = (_k) + 0.5 _k$ 。
所有层的奖励累加，优化模型参数。
训练时，加入噪声使层输出随机，模拟 RL 的探索。

处理相似物体：增加惩罚项，奖励函数可为： \[ r_k = \text{mean\_IoU}_k + \alpha \times \text{accuracy}_k - \gamma \times \text{overlap\_penalty} \] 其中 overlap_penalty 是预测框之间 IoU 过高的惩罚，鼓励模型区分相近物体。

如何将$A_i$应用于目标检测？

$A_i$是优势函数，相当于序列打分函数。在目标检测中：

候选框和分类打分：对每层解码器生成的候选框和分类进行打分，打分基于奖励 $r_k$，如 IoU 和分类准确度。
如何成为序列信息：将 DETR 解码器看作序列过程，$o_1, o_2, \ldots, o_{t-1}, o_t, \ldots$代表每层的对象查询更新。每个 $o_t$是当前层的输出（候选框和分类），序列信息通过层间传递实现：
- 状态$q_t$ 是第 $t$ 层对象查询，动作 $o_t$ 是更新到 $q_{t+1}$，概率为 $\pi_{\theta}(o_t|q_t)$。
- 优势 $A_i = r_i - b_i$，其中 $b_i$ 是基线（如批次平均奖励）。

模型和符号定义：

符号	说明
$q$	输入状态，目标检测中为图像特征或对象查询。
$\pi_{\theta}(o\|q)$	策略分布，模型输出动作 $o$ 的概率，$o$ 为对象查询更新。
$\pi_{\theta_{old}}(o\|q)$	上一轮策略分布，用于比率计算。
$o_i$	第 i 个样本的动作，目标检测中为第 t 层的对象查询更新。
$G$	样本组大小，通常为批次大小。
$A_i$	优势函数，基于奖励$r_i$ 和基线 $b_i$，$A_i = (r_i - b_i)/std(r_i)$。
$\epsilon$	裁剪参数，控制策略更新范围，通常为 0.2。
$\pi_{ref}$	参考策略，用户指定为 ground truth（标注的 label 信息），目标检测中为真实框和类别分布。
$\beta$	KL 散度的权重，控制分类损失强度。

符号	说明
\(q\)	输入状态，目标检测中为图像特征或对象查询。
\(\pi_{\theta}(o\|q)\)	策略分布，模型输出动作 \(o\) 的概率，\(o\) 为对象查询更新。
\(\pi_{\theta_{old}}(o\|q)\)	上一轮策略分布，用于比率计算。
\(o_i\)	第 i 个样本的动作，目标检测中为第 t 层的对象查询更新。
\(G\)	样本组大小，通常为批次大小。
\(A_i\)	优势函数，基于奖励\(r_i\) 和基线 \(b_i\)，\(A_i = (r_i - b_i)/std(r_i)\)。
\(\epsilon\)	裁剪参数，控制策略更新范围，通常为 0.2。
\(\pi_{ref}\)	参考策略，用户指定为 ground truth（标注的 label 信息），目标检测中为真实框和类别分布。
\(\beta\)	KL 散度的权重，控制分类损失强度。

2025-3-13-模型构建

状态定义

动作定义

奖励定义

优化过程

如何将\(A_i\)应用于目标检测？