2025-3-4-为什么DETR中要使用匈牙利算法???
匈牙利算法:Kuhn, H. W. “The Hungarian Method for the Assignment Problem.” Naval Research Logistics Quarterly, pp. 83–97, https://doi.org/10.1002/nav.3800020109.
DETR:Carion, Nicolas, et al. “End-to-End Object Detection with Transformers.” Computer Vision – ECCV 2020,Lecture Notes in Computer Science, 2020, pp. 213–29, https://doi.org/10.1007/978-3-030-58452-8_13.
记录下今天讨论的问题。感想是,交流有助于理解,一些可能需要很久能想通的问题(=-=)
DETR
目标检测=集合预测
- 新目标函数:理想情况下每个物体只生成一个框(二分图匹配)
- 使用了Transformer,额外有learned pbject query(类似anchor)
- 并行(无法自回归),实效性高
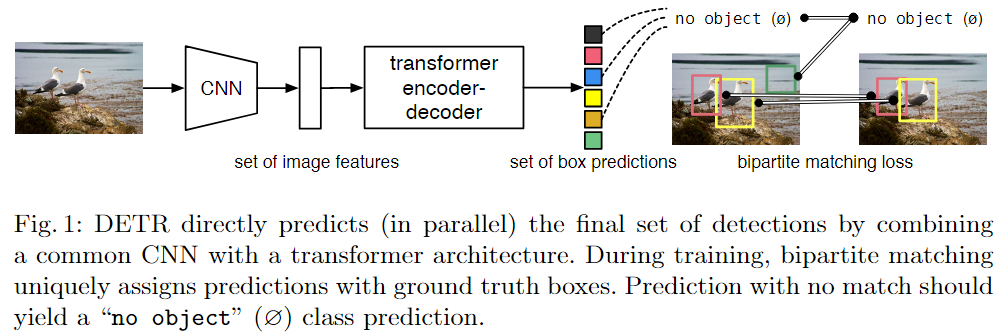
DETR流程:先使用CNN提取特征,拉直特征,进入Transformer
Transformer作用:进一步学习全局的信息。
- encoder:每一个点/特征与图片中其他特征进行交互。这样就能大概知道哪块是哪个物体,全局的特征有利于移除冗余的框。
- decoder:额外输入object query限定出多少个框(有点像anchor)
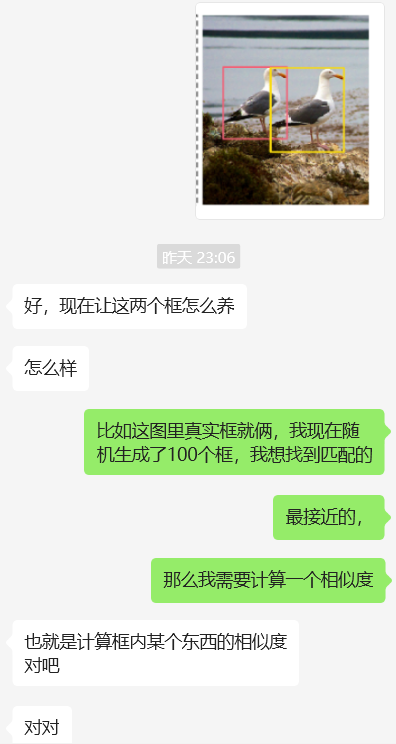
e.g.比如object query=100,那么就会固定输出100个框,然后使用二分图匹配的方法,找到对应(合适)的框,比如上图中,就只找到了两个框是对应的;那么剩下的98个框都被标记为”No object”。
推理:前面步骤一致,得到100个框。但是没有匹配的过程,直接在输出的100个框这里用阈值卡输出的置信度。比如置信度>0.7的作为前景物体。
缺陷:大物体结果好(归因于使用了Transformer);小物体结果不行。Deformable DETR解决了。
相关工作:集合预测+Transformer-Parallel+目标检测
Learnable NMS等等使用人工干预。基于集合的目标函数。DETR不想用过多的先验知识。
模型架构
DETR的模型的输出,是一个固定的集合。
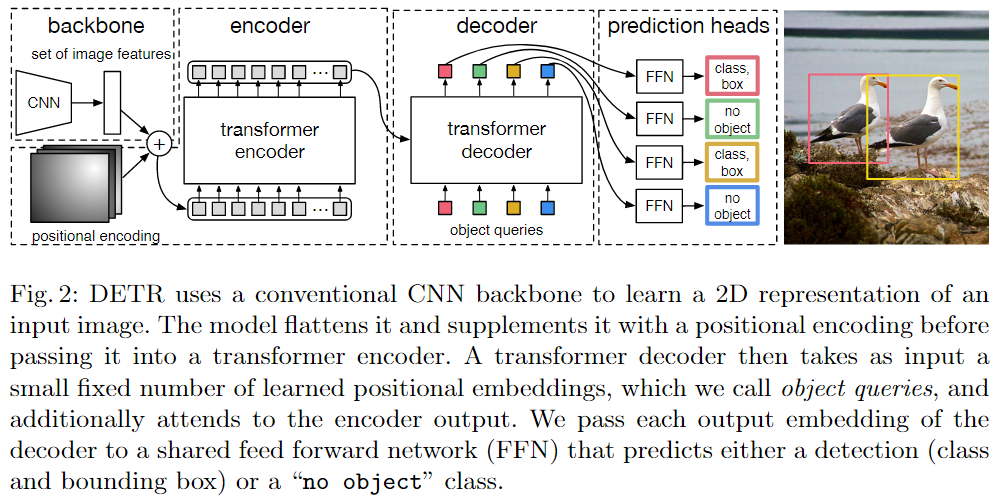
假如输入图片是3x800x1066—CNN—>2048x25x34—1x1降维—>256x25x34+位置编码256x25x34
—$\bigoplus$—>850x256—Transformer Encoder—>850x256(作为KV)
Q:100x256+KV:800x256—Transformer Decoder—>100x256—FFN(100个)
全连接层FFN进行两种预测:出框1x4+类别预测COCO:1x91
出框+分类后,使用匈牙利算法计算loss,梯度反向回传,进行更新模型。
- object query自注意力操作:不能省、移除冗余框。
- 计算loss:为了计算更稳定,在每个decoder后面加了auxiliary loss。
目标函数
其中,$\hat{\sigma}$是要优化求解的一个排列,$\mathfrak{S}_N$表示$N$个元素的所有排列的集合。$\arg\min$表示取使得后面求和式最小的$\sigma$值。$\mathcal{L}_{\text{match}}(y_i,\hat{y}_{\sigma(i)})$是一个匹配损失函数,用于衡量真实值 $y_i$ 和经过排列$\sigma$后的预测值$\hat{y}_{\sigma(i)}$之间的差异,$i$从$1$到$N$进行求和。
其中,$\mathbb{1}_{\{c_i\neq\varnothing\}}$是指示函数,当条件$c_i\neq\varnothing$成立时,函数值为$1$,否则为$0$。$\hat{p}_{\sigma(i)}(c_i)$ 是与类别相关的预测概率,$\mathcal{L}_{\text{box}}(b_i,\hat{b}_{\sigma(i)})$是用于衡量边界框 $b_i$(真实边界框)和$\hat{b}_{\sigma(i)}$(预测边界框)之间差异的损失函数。
这是我们的真·目标函数。$\mathcal{L}_{\text{Hungarian}}(y,\hat{y})$表示匈牙利匹配损失函数,$y$和$\hat{y}$分别代表真实值和预测值集合。对$i$从$1$到$N$进行求和,每一项中$-\log\hat{p}_{\hat{\sigma}(i)}(c_i)$ 可能是对类别预测概率取负对数,$\mathbb{1}_{\{c_i\neq\varnothing\}}\mathcal{L}_{\text{box}}(b_i,\hat{b}_{\hat{\sigma}(i)})$含义同第二个公式中对应部分,即根据条件决定是否计算边界框损失 。
代码
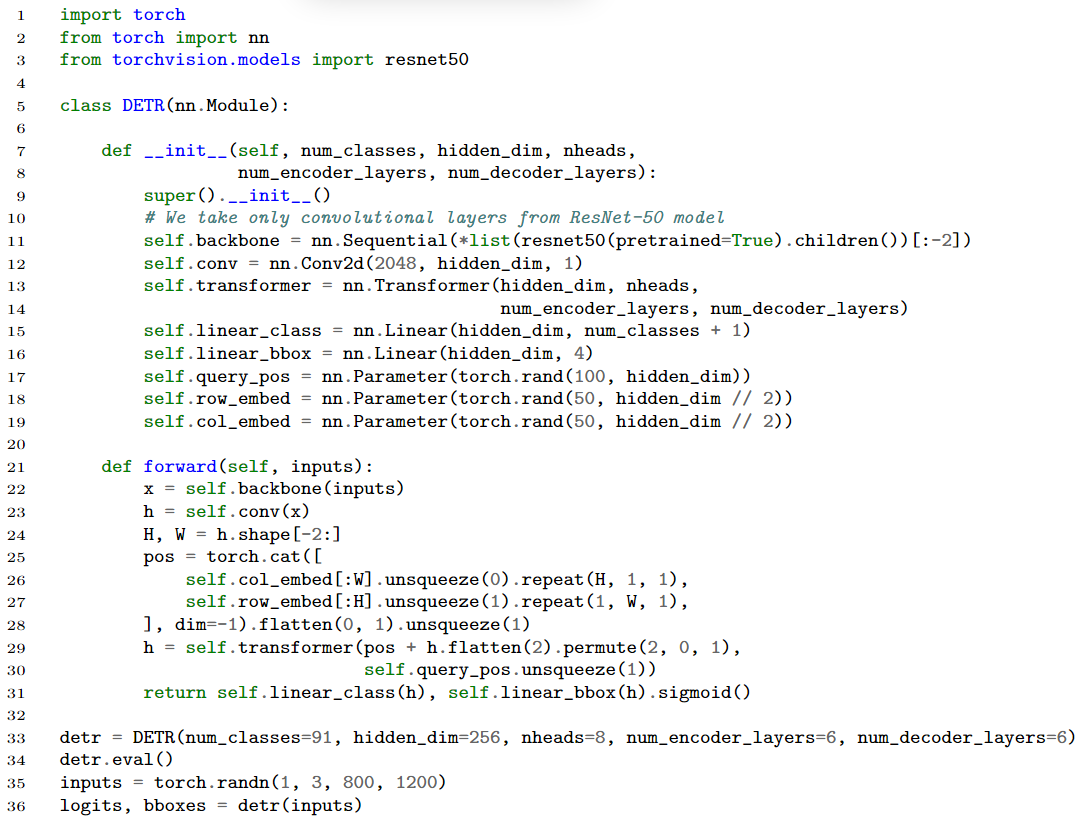
1 | import torch |
探讨:为什么DETR中要使用匈牙利算法???
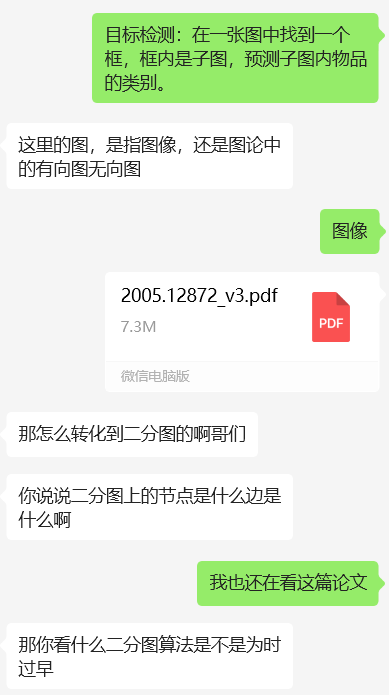
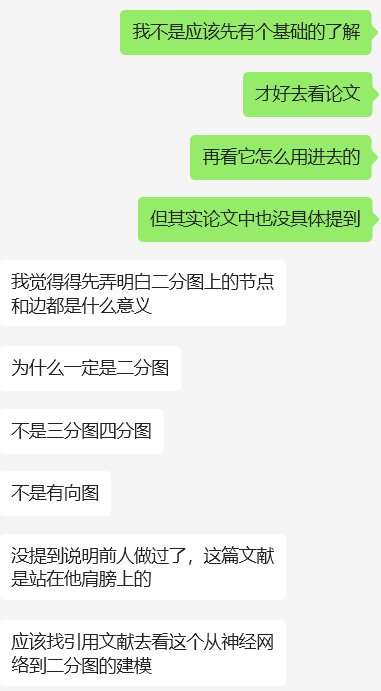
- 这个问题背景下如何与图论挂钩、匹配上匈牙利算法?
- 还能使用其他的算法完成吗?
仅给出个人意见:
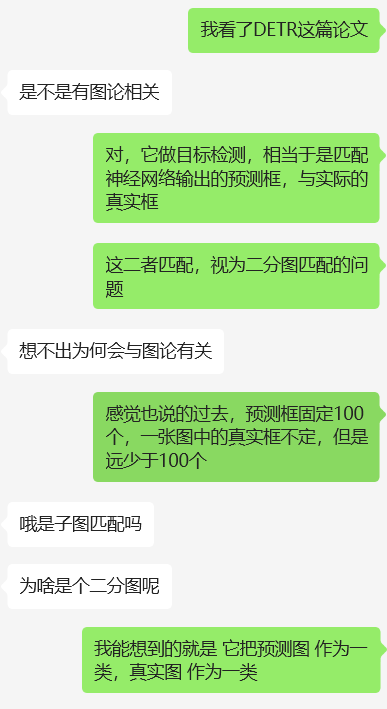
DETR论文中做目标检测时,将神经网络输出的预测框与实际真实框的匹配视为二分图匹配问题。比如,预测框固定100个,一张图中真实框数量不定且远少于100个($\ll 100$)。将预测图和真实图各作为一类,以此构建二分图。
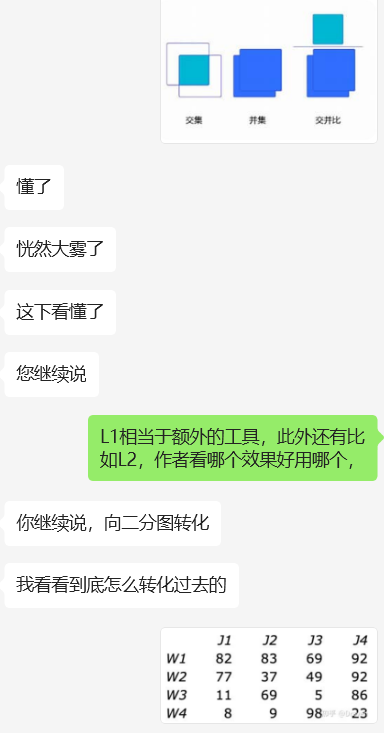
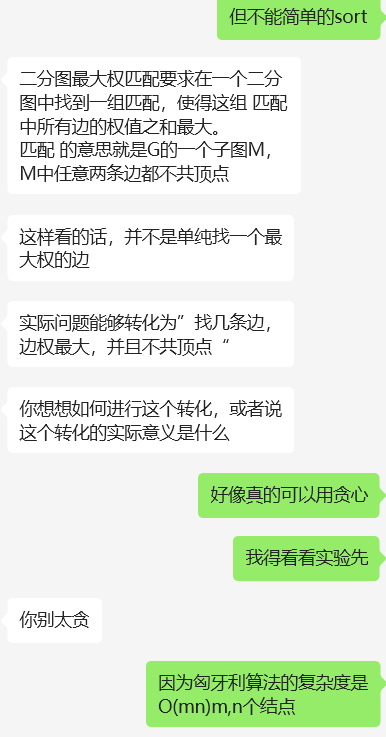
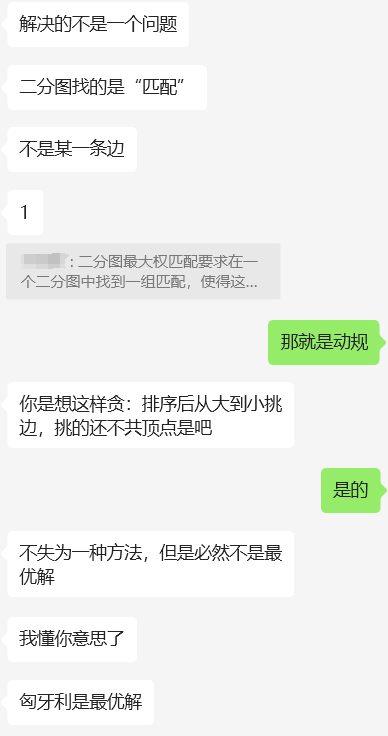
二分图最大匹配:在二分图中,行列代表两个类别的结点,将计算出的loss值作为边的权重填入,边表示两个图(框)之间的匹配度(相似度)。该问题转化为二分图最大权匹配问题,即要在二分图中找到一组匹配,使得这组匹配中所有边的权值之和最大,且匹配的边不共顶点。
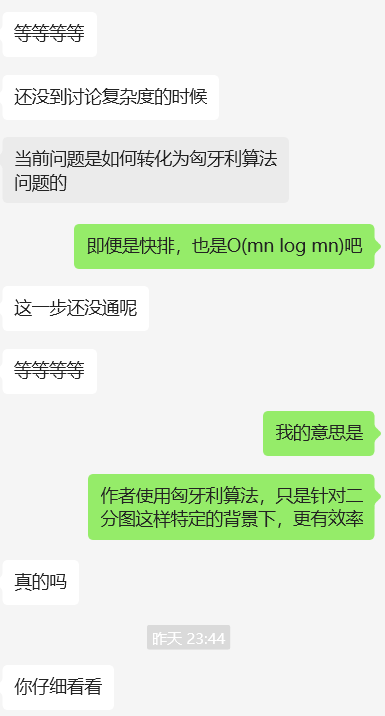
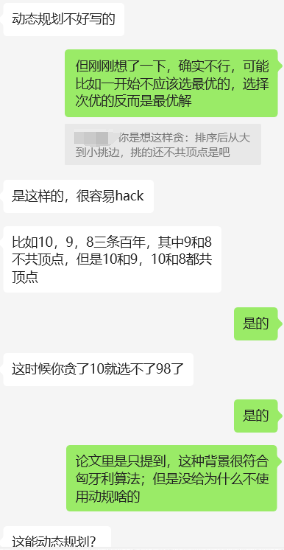
一开始我以为可以用贪心算法(排序后从大到小挑边且不共顶点)或sort解决,但发现这样会落入局部最优、可能找不到全局最优。
然后又想,这是不是能用动态规划做?但是经过思考,这个不具有最优子结构的问题,所以不能动态规划做。
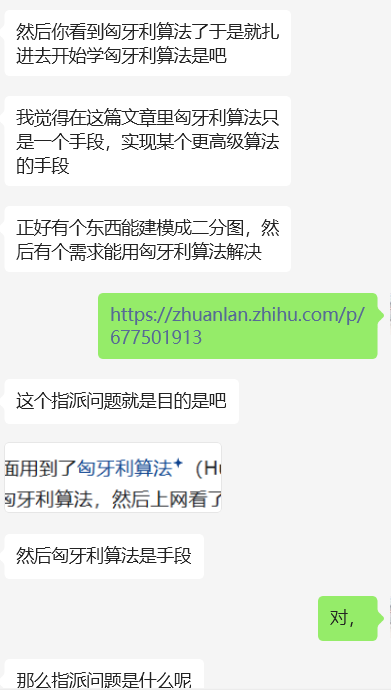
这就是一个单纯的图论的问题+有一定的限制条件(loss作为边权、每个任务匹配一个员工),所以是最大流问题/二分图最大匹配。所以除了匈牙利算法之外,能够解决最大流问题的算法都能使用,只是作者选择了匈牙利算法。
一些原纪录: