模式识别-Ch9-数据聚类

Ch9 数据聚类

[TOC]

距离与相似性度量

设

距离度量	对应公式
Minkowski距离
曼哈顿距离(城市距离)
欧式距离
切比雪夫距离
Mahalanobis距离(马氏距离)

K-means

无监督学习

K-means算法步骤

算法复杂度：每次迭代的计算复杂度：

1. 为每个点分配到最近的中心点：需要计算所有点到每个中心的距离，复杂度为。
2. 更新每个簇的中心：对每个簇内的点计算均值，复杂度为。

1. 输入：N 个样本： ，每个样本 是 维的。K：划分的簇数。

2. 初始化：初始化 K 个簇的中心：，每个 。

   • 通常这些中心是随机初始化的，但有更好的初始化方法，例如K-means++（可以提高算法收敛速度和稳定性）。

3. 迭代步骤：

   • (Re-)分配样本：对每个样本 ，找到最近的簇中心：

     $$C_k = \{n : k = \arg\min_k \|x_n - \mu_k\|^2\}$$

     表示欧几里得距离的平方。每个样本 会被分配到距离最近的簇 。

   • 更新簇中心：对每个簇 ，重新计算其中心为：

     $$\mu_k = \text{mean}(C_k) = \frac{1}{|C_k|} \sum_{n \in C_k} x_n$$

     |C_k| $是第 k 个簇中样本的个数。

   • 重复：重复上述两步（分配和更新），直到算法收敛。即：当簇的中心或“损失”（通常指平方误差的总和）不再显著变化时，算法停止。

损失函数

• K个簇的中心：

• ：若数据点 属于簇 ，则 ；否则 。

• one-hot encoding: 是数据点属于哪个簇的独热编码.

单个点 的损失是与其最近的簇中心 的平方欧氏距离：

$$\ell(\mu, x_n, z_n) = \sum_{k=1}^K z_{nk} \| x_n - \mu_k \|^2$$

全部样本点的损失是单点损失的累加：

$$L(\mu, X, Z) = \sum_{n=1}^N \sum_{k=1}^K z_{nk} \| x_n - \mu_k \|^2\\L(\mu, X, Z) = \| X - Z \mu \|^2$$

其中， 是 的分配矩阵， 表示数据点 属于第 个簇。

优化目标：最小化上式，即最小化簇内的点到簇中心的平方距离之和。

• 这是一个 非凸目标函数（non-convex objective function），意味着可能有多个局部最优解。也是NP-hard问题。

  

• K-means 的求解是一个 启发式方法，不能保证找到全局最优解。

• 优化过程：分步交替优化 (alternating optimization)：

  1. 固定簇中心 ，优化点的簇分配 （将每个点分配到最近的簇中心）。
  2. 固定簇分配 ，优化簇中心 （重新计算每个簇的均值）。

K-means 的收敛性

收敛性：

• K-means在有限次迭代后必然收敛（目标函数值不再变化）。
• 但收敛的速度与初始化的好坏有关。

收敛过程：

• 更新点的分配 ：
  • 将 重新分配到最近的簇中心：
  • 这一步会使得目标函数 不增加，即：
• 更新簇中心 ：
  • 重新计算每个簇的中心：
  • 这一步也会使目标函数 不增加：
• 整体收敛性：因为目标函数 在每次迭代中单调减少，而 有下界 (即大于或等于 0)，所以 K-means 最终会收敛到一个局部最优解。

局限性

• 硬分配问题：K-means是硬分配，每个点要么完全属于一个簇，要么完全不属于，这样可能忽略了实际中的模糊性。而软分配（如高斯混合模型GMM）可以用概率分配点到簇中。

  • 示例：点可能属于3个簇的概率分别是0.7、0.2、0.1。

• 类大小不均的问题：K-means只在类大小差不多时表现良好。对于大小非常不均的簇，可能会造成问题。

• 形状限制问题：K-means只适用于圆形或凸状的簇，对于非凸簇形状的分割表现不好。
  • 解决方法：Kernel K-means或者Spectral Clustering可以解决非凸形状问题。

K值选择

K-means是启发式算法，初始化的中心点对最终结果有很大影响。

问题：如果初始点选择得不好，可能会陷入局部最优，如某些点会错误地分配到不合适的簇中。

解决方案：

• 使用K-means++等初始化方法（对初始点进行优化）。
• 引入基于方差的split/merge操作。

or

方法1：交叉验证：通过交叉验证选择最优的K值。

• 问题：如何定义优化目标？常用的是簇内误差和簇间距离。

方法2：专家判断：让领域专家观察聚类结果，判断是否合适。

• 问题：如何展示结果？高维空间中的数据点可能难以可视化。

方法3：肘部法则（The “knee” solution）：

• 绘制不同K值对应的目标函数值（如SSE），选择拐点位置的K值。
• 拐点反映的是增加K值后收益的递减。

总结

算法步骤

K-means是一种无监督聚类算法，用于将数据划分为K个簇。其步骤如下：

1. 初始化：随机选择K个点作为初始簇中心（可以用K-means++优化初始化）。
2. 迭代过程：
   • 分配点到最近的簇：将每个数据点分配到距离最近的簇中心（基于欧几里得距离）。
   • 更新簇中心：重新计算每个簇内所有点的均值，作为新的簇中心。
3. 停止条件：当簇中心不再改变或目标函数收敛时，停止迭代。

损失函数

K-means的目标是最小化簇内平方误差（SSE），其损失函数为：

$$L(\mu, X, Z) = \sum_{n=1}^{N} \sum_{k=1}^{K} z_{nk} \|x_n - \mu_k\|^2$$

其中，表示第个点属于第个簇。

影响K-means算法的因素

1. 初始中心点：初始中心点选择对K-means收敛到全局最优还是局部最优有很大影响。

• 优化方法：使用K-means++，通过分布式选择初始点来提高性能。

2. K值的选择：K值直接决定了聚类的数量。

• 选择方法：
  • 肘部法则（The elbow method）：通过观察SSE随K变化的拐点来确定。
  • 交叉验证（Cross-validation）：根据验证误差选择最优K值。
  • 专家判断：结合领域知识手动选择K值。

3. 数据分布：数据点的密度、形状、类间距离都会影响K-means效果。

• 适用场景：K-means在类大小相等、分布均匀、簇为凸形时效果最好。
• 问题场景：当簇的形状为非凸时（如月牙形分布），K-means表现较差。

4. 距离度量：K-means默认使用欧几里得距离，如果数据特征不同或含噪声，需要归一化处理。

优缺点分析

优点：K-means假设数据点是紧凑、均匀分布的簇。K-means倾向于处理形状规则的簇，对紧凑性要求高。

Compactness（紧凑性）：目标是优化数据点与簇中心之间的紧凑性。

收敛性保证：算法必然在有限次迭代后收敛（虽然可能收敛到局部最优）。

缺点

1. 需要指定K值：K值需要事先给定，难以确定最佳K值。
2. 对初始中心敏感：不同的初始中心可能导致不同的聚类结果，可能陷入局部最优。
3. 对簇形状限制：只能处理凸形簇，无法处理非凸簇或复杂形状的簇。
4. 对噪声和异常值敏感：噪声点可能会显著拉偏簇中心。
5. 难以处理类大小不均的问题：在类大小差异较大的情况下，较小的类可能被忽略。

改进方向

1. 优化初始中心：使用K-means++或其他启发式方法选择初始点。
2. 扩展为非凸形状：使用Kernel K-means或Spectral Clustering。
3. 处理噪声数据：引入模糊聚类（如Fuzzy C-means）来实现软分配。
4. 自动选择K值：使用肘部法则、轮廓系数等自动选择合适的K值。

分级聚类(Hierarchical Clustering)

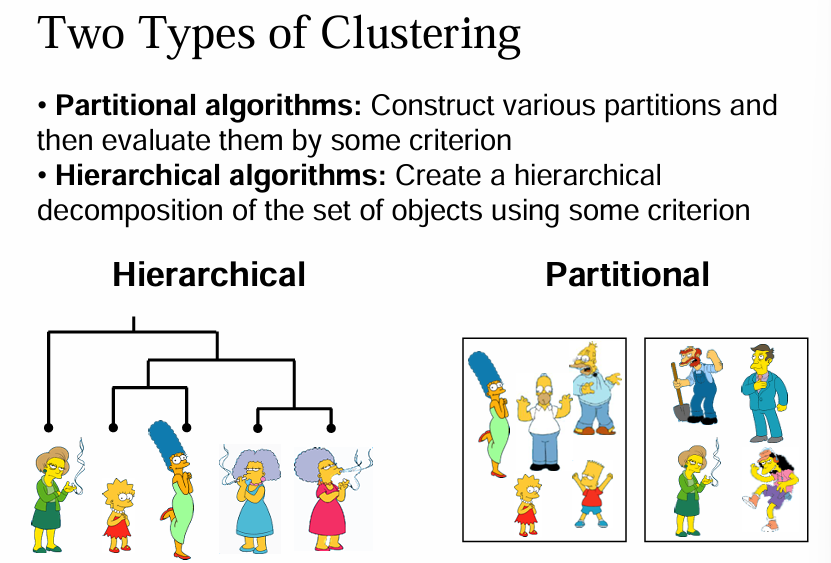
分级聚类思想：对于 n个样本，极端的情况下，最多可以将数据分成n类;最少可以只分成一类，即全部样本都归为一类。

• 凝聚的层次聚类(自底向上)：将每个样本作为一个簇，然后根据给定的规则逐渐合并一些样本，形成更大的簇，直到所有的样本都被分到一个合适的簇中。
• 分裂的层次聚类(自顶向下)：将所有的样本置于一个簇中，然后根据给定的规则逐渐细分样本，得到越来越小的簇，直到某个终止条件得到满足

这个很像昨天(2024.12.10)上多元统计分析介绍的:

好巧，都是在讲聚类分析:D)

分级聚类的两个核心问题：

1. 度量样本之间的距离(相似性)
2. 度量两个簇之间的距离(相似性)

度量样本之间的距离(相似性)？

1. 距离：欧式距离、马氏距离、曼哈顿距离、匹配距离…
2. 相似性：相关系数、高斯相似性函数、余弦相似度、距离倒数…

簇与簇之间的距离：

距离类型	公式
最小距离	$d_{\text{min}}(D_i, D_j)=\min_{x\in D_i, x’\in D_j}\	x - x’\	$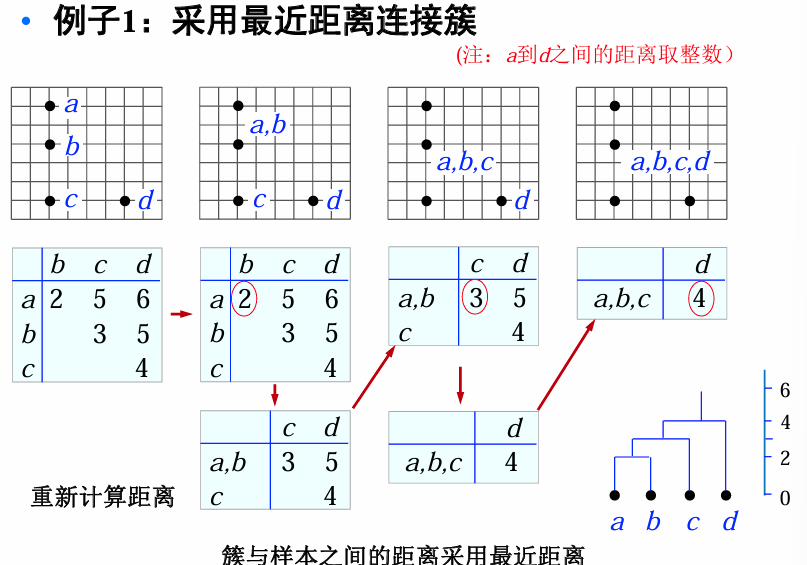
最大距离	$d_{\text{max}}(D_i, D_j)=\max_{x\in D_i, x’\in D_j}\	x - x’\	$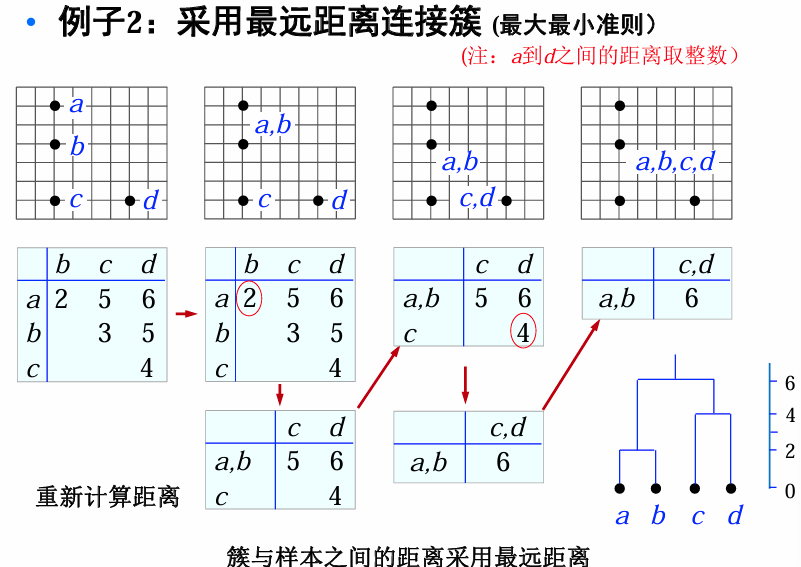
平均距离	$d_{\text{avg}}(D_i, D_j)=\frac{1}{\	D_i\	\	D_j\	}\sum_{x\in D_i}\sum_{x’\in D_j}\	x - x’\	$
中心距离	$d_{\text{mean}}(D_i, D_j)=\	m_i - m_j\	$

例：最小距离准则

有如下6个样本：

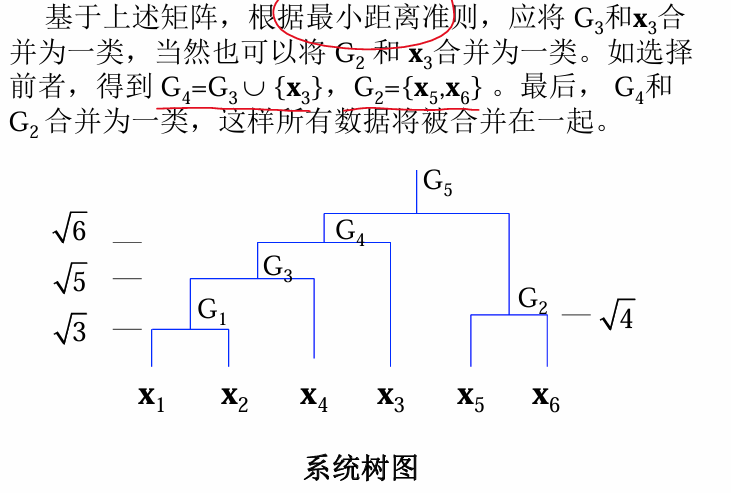
分级聚类好处

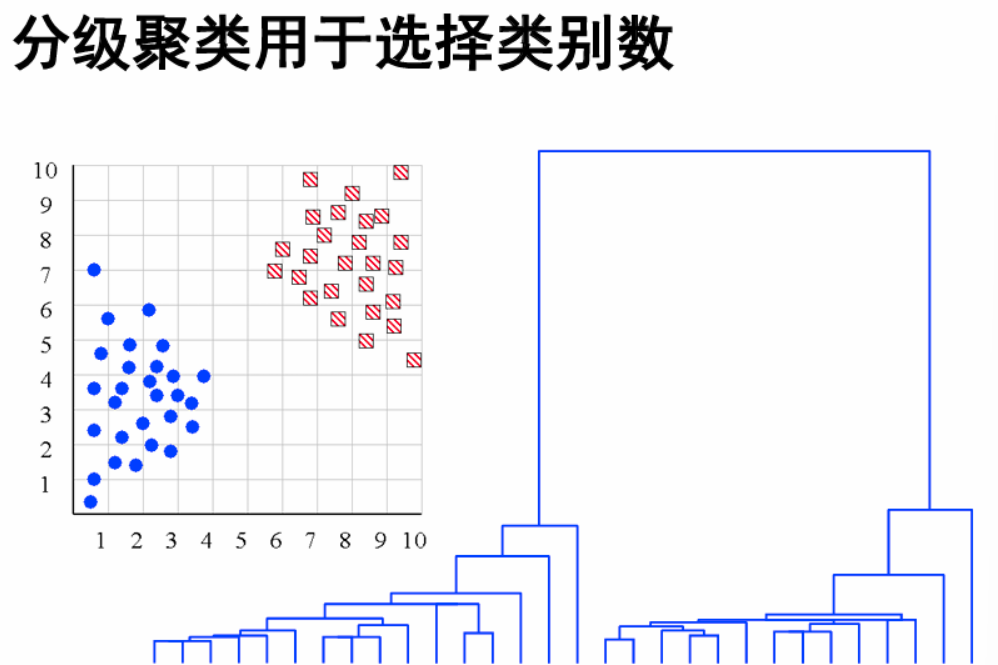
1. 根据观察聚类树，选择合适的类别数。(而不是事先指定)

   根据这个树：最后一次合并的时候得到的距离，相较于之前进行聚类的距离来说，比较大，暗示可能是两类。

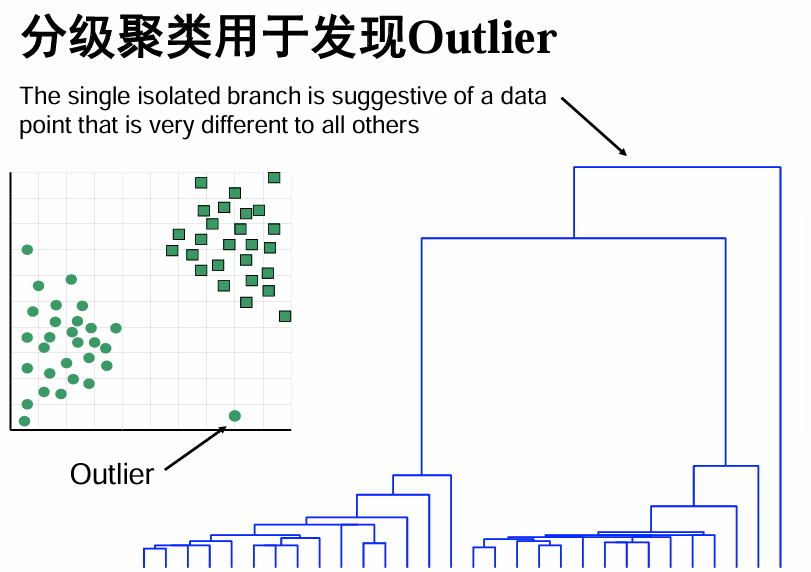
1. 发现野点

Summary	详细说明
1. 无需事先指定簇的数量	用户可以在生成的层次树形结构（树状图，dendrogram）上根据实际需求来决定截断点，从而得到期望的簇数。
2. 层次结构直观匹配人类直觉	层次聚类会逐步将样本聚合（或拆分），最终构建出一个层次分明的树形结构。
3. 扩展性较差，时间复杂度高	层次聚类一般有至少 O(n²) 的时间复杂度（n 为数据点个数）。
4. 存在局部最优问题	本质上是一种启发式搜索过程，从局部合并（或分裂）开始，不能保证找到全局最优的聚类结构。它可能在局部最优的决策上停滞，从而影响最终结果的质量。
5. 结果解释具有主观性	虽然层次聚类能给出一个清晰的树状层次结构，但怎样选择合适的层次截断点来定义簇的数量和分布往往依赖经验、领域知识或特定的评价指标。

谱聚类(Spectral Clustering)

基本原理、影响因素、步骤

谱学习方法：广义上讲，任何在学习过程中应用到矩阵特征值分解的方法均叫谱学习方法，比如主成分分析(PCA)、线性判别分析(LDA)、流形学习中的谱嵌入方法、谱聚类等等。

谱聚类：谱聚类算法建立在图论的谱图理论基础之上，其本质是将聚类问题转化为一个图上的关于顶点划分的最优问题。谱聚类算法建立在点对相似性基础之上，理论上能对任意分布形状的样本空间进行聚类。

图论基本概念

对于这个显然对称(W对称-D对角)的拉普拉斯矩阵有两种归一化方式：

如果在任务中需要对称性或者特征分解，选择对称归一化；如果需要建模随机游走或信息传播过程，则使用非对称归一化。

• 对称归一化（Symmetric Normalized Laplacian）：

$$L_{\text{sym}} = D^{-1/2} L D^{-1/2} = I - D^{-1/2} W D^{-1/2}$$

• 非对称归一化（Random Walk Normalized Laplacian）：

$$L_{\text{rw}} = D^{-1} L = I - D^{-1} W$$

特性	对称归一化（Symmetric）	非对称归一化（Random Walk）
归一化方式
矩阵特性	对称	非对称
适用场景	谱聚类、图神经网络	随机游走、转移概率建模
特性平衡	平衡了节点间的影响	偏重节点的方向性和流动性
数学操作复杂度	更易处理，特征值分解简单	更复杂，适合概率模型

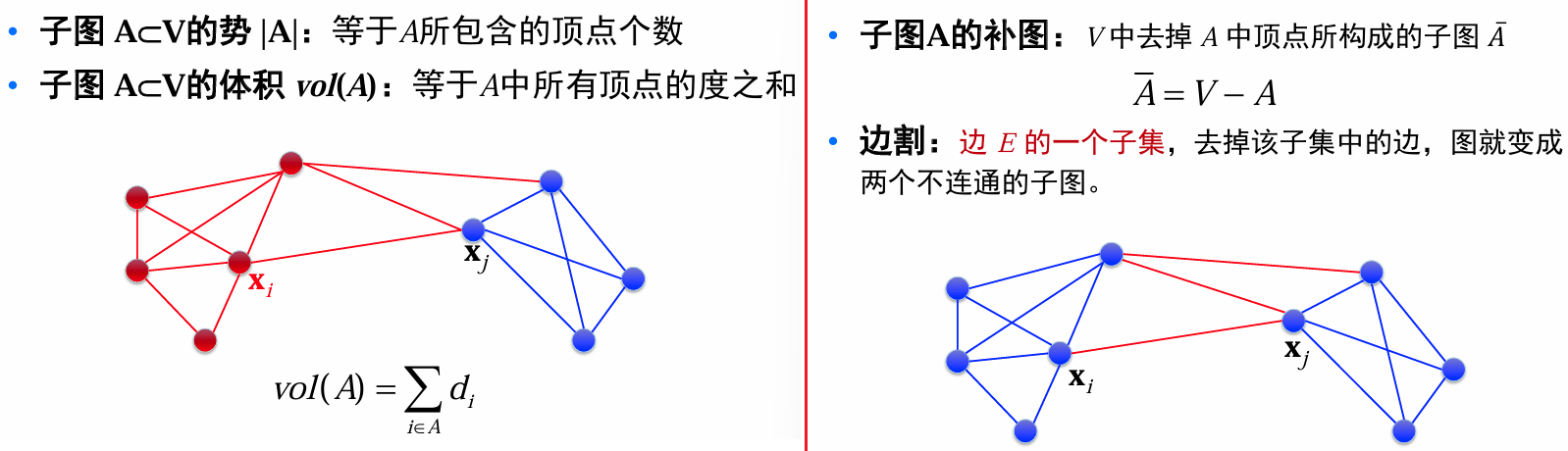
图分割(Graph partitioning)

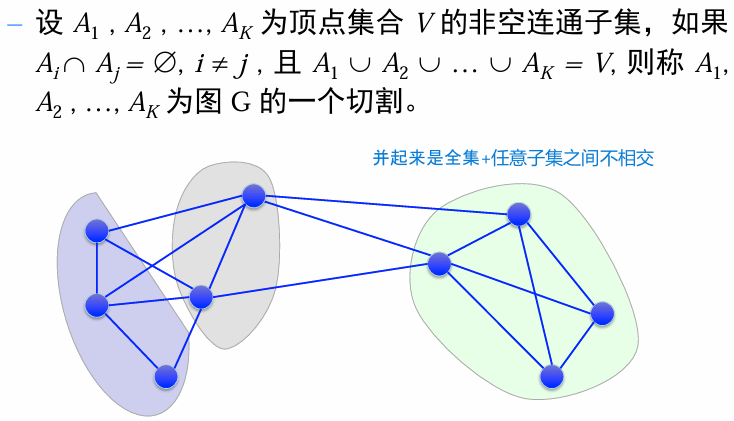
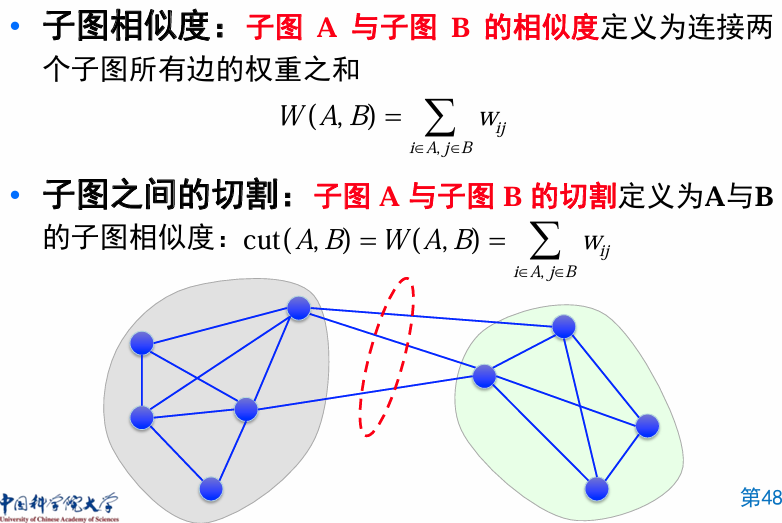
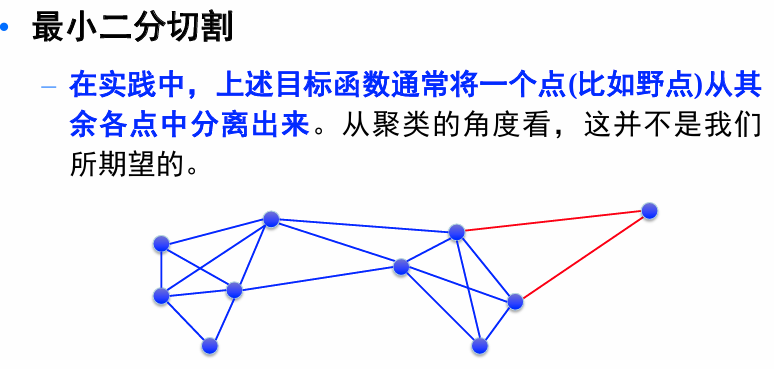
Mincut Problem：即如何将图分割成 K 个子集 ，以最小化切分边的总权值。这里的目标是优化图的分割，使得子集之间的连接尽可能少，从而减少交互的“成本”。

$$cut(A_1,A_2,\dots,A_k)=\sum^K_{i=1}W(A_i,\bar A_i)\\ W(A_i,\bar A_i) = \sum_{p\in A_i,q\in\bar A_i}w_{pq}$$

其中， 是第 iii 个子集 AiA_iAi 和其补集 之间的权值和。

谱聚类

核心思想：

• 使用相似性图（Similarity Graph）来表示数据点之间的关系。
• 构造图的拉普拉斯矩阵（Laplacian Matrix），对其进行特征值分解，提取重要的特征向量作为新的数据表示。
• 将这些特征向量视为降维后的特征空间，再在特征空间中应用传统的聚类算法（如K-means）。

主要算法

主要步骤：

1. 构建相似性图W、计算度矩阵(根据W)
2. 计算拉普拉斯矩阵：有不同的方法 归一化/未归一化
3. 计算前k个特征值对应的特征向量
4. K-means聚类：将矩阵 U 的行看作新的数据点，将其视为在 k维空间的嵌入表示。

1. 未归一化的谱聚类算法（Unnormalized Spectral Clustering）：

• 构造相似性图并计算未归一化的拉普拉斯矩阵 L。
• 提取拉普拉斯矩阵的前 k 个最小特征值对应的特征向量，组成矩阵 U。
• 每个数据点对应矩阵 U 的一行，在这个新特征空间中使用 K-means 聚类。

2. 归一化的谱聚类算法（Normalized Spectral Clustering） [Shi2000]:

• 基于随机游走拉普拉斯矩阵 。
• 步骤类似，但拉普拉斯矩阵需要归一化以调整权重分布。

3. 改进的归一化谱聚类算法 [Ng2002]:

• 使用对称归一化拉普拉斯矩阵 。
• 特点是对特征向量进一步归一化（行归一化到单位范数），使得特征空间更平衡。

优缺点

谱聚类的目标是基于数据点的连通性（图论中的相似性图）进行聚类。

优点：

谱聚类的连接性很好。谱聚类对环形或其他非凸形状簇的聚类效果更好，而K-means在这种情况下效果较差。

谱聚类能够更好地处理非凸形状的簇，因为它基于图的连通性，而不是欧几里得距离。