模式识别-Ch8-模型选择与集成学习
Ch8 模型选择与集成学习

[TOC]

模型选择原则
Occam剃刀原理 (Occam’sRazor):(简单有效)若无必要、勿增实体
没有免费的午餐定理 (NoFreeLunch,NFL): 对“寻找代价函数极值”的算法,在平均到所有可能的代价函数上时,其表现都恰好相同。
对于整个函数集(类)而言,不存在万能的最佳算法。所有算法在整个函数集的平均表现度量是一样的。
特别地,如果算法A在一些代价函数上优于算法B,那么存在一些其它函数,使B优于A。
样本划分:交叉验证
交叉验证是目前最常用的一种模型选择和评估方法 (特别是 对模型的参数进行选择)。
分k个、进行k次。
交叉验证:将样本平分为k个子集,用k-1个子集进行训练,余下的部分用于验证、并计算验证误差。重复这一过程k次,得到k次结果的平均。
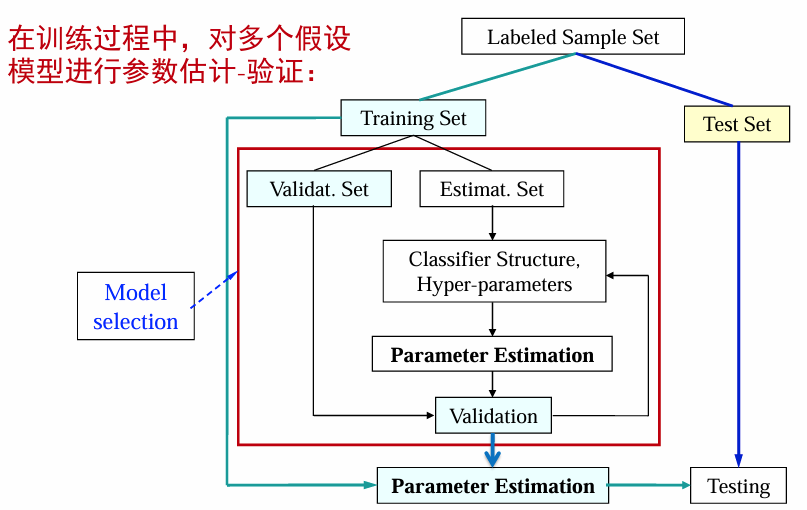
基于交叉验证的模型参数选择:
- 给出参数的候选集合
- 对每个参数,将训练集使用k-折交叉验证
- 根据验证误差,选择统计性能最优的参数作为模型参数
Adaboost(Adaptive boosting)
统计学习方法,提高给定算法准确度,三个臭皮匠顶个诸葛亮
分类问题:改变训练样本的权重、学习多个分类器、将这些分类器组合。
强可学习vs弱可学习
强学习:一个概念/类,若存在一个多项式的学习算法能够学习它,且正确率很高。
弱学习:弱存在一个多项式的学习算法能够学习它,但学习正确率仅比随机猜测略好。
强可学习与弱可学习是否等价?
如果等价,则可以将弱可学习通过“提升”变成强可学习,这 样可以避免直接寻找强可学习算法。
方法
核心思想:给定训练集、寻找比较粗糙的分类规则(弱分类器),然后组合弱分类器=强分类器。
测量:改变训练数据的概率(权重)分布,针对不同 的训练数据的分布,调用弱学习算法来学习一系列分 类器。
两个基本问题
Q1:在每轮训练中,如何改变训练数据的权值or分布?
A1:提高被前一轮弱分类器分错的样本的权重,降低被正确分类的样本的权重。于是,错分的样本将在下一轮弱分类器中得到更多关注,分类问题被一系列弱分类器“分而治之”。
Q2:如何将一系列的弱分类器组合成一个强分类器?
A2:采用加权投票的方法。具体地,按照弱分类器的分类错误率对其加权,错误率较小的弱分类器获得较大的权重,使其在表决中起更大作用。
Adaboost算法
给定一个两类分类训练数据集:
其中每个样本都由实例和label组成。
输入弱学习算法:
初始化数据的权值分布:
(共有M个弱分类器) 使用具有权值分布
的训练数据,学习弱分类器: 计算
在训练数据集上的加权分类错误率: 计算
的贡献系数: 更新训练数据集的权值分布:
构建弱分类器的线性组合:
对于二分类问题,最终的分类器:
算法说明
初始权重相等都是
反复学习多个弱分类器:
计算加权分类错误率:
在加权训练数据集上的分类错误率是被其错分样本的权值之和。 其中
是第m轮第i个实例的权值,且 计算贡献系数
: 是 的单调递减函数,分类错误率越小的弱分类器在最终分类器中的作用越大。 更新权重系数,具体计算:若正确分类,则减少权重;否则,则增加权重(错分类样本权重扩大
倍)。 是归一化因子,它使 成为一个概率分布: 
线性组合
实现对M个弱分类器的加权表决。系数 表示弱分类器 的重要性。PS:所有 之和 的符号决定实例/样本 的类别、绝对值表示分类的置信度。

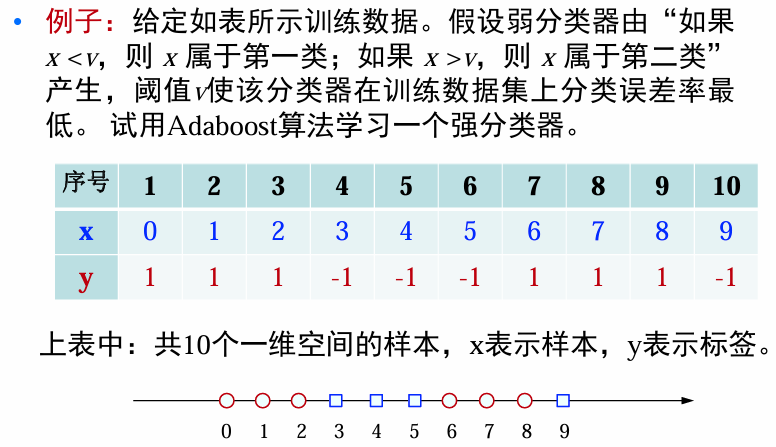
例