模式识别-Ch7-特征提取与特征选择

Ch7 特征提取与特征变换

[TOC]

引言

特征提取的目的	特征变换的目的
提取观测数据的内在特性	降低特征空间的维度，增加数据密度、降低过拟合 风险
减少噪声影响	便于分析和减少后续步骤的计算量
提高稳定性	减少特征之间可能存在的相关性、有利于分类

特征提取

提取对象	提取方式
语音特征提取	局部特征提取方法：LBP, SIFT
文本特征提取	全局特征提取方法：词袋模型, HoG
视觉特征提取	—-

特征变换：根据特征变换关系不同

线性特征变换	非线性特征变换
采用线性映射将原特征变换至一个新的空间（通常维度更低）	采用非线性映射将原特征变换至一个新的空间（通常性能更好）
PCA,LDA,ICA	KPCA,KLDA,Isomap,LLE,HLLE,LSTA

特征提取

文本特征提取

将文本内容转化为向量的过程。将一个文档表示成一个向量，向量的相似性反应文档的相似性。

向量空间模型(BOW, TF-IDF)

词向量模型(word2vec)

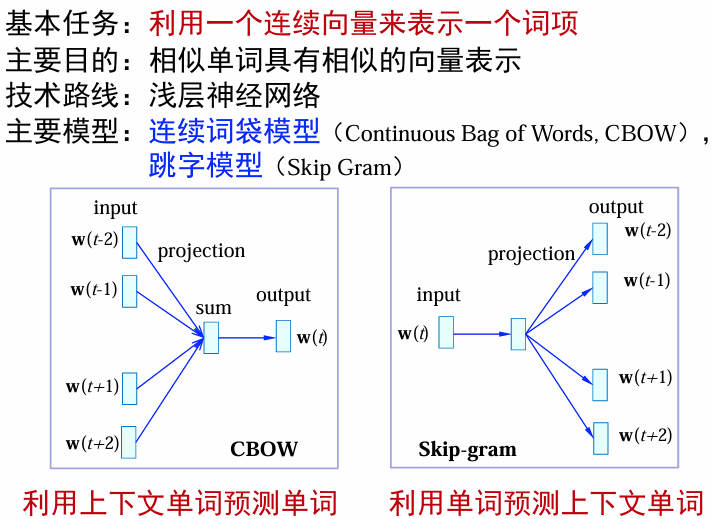
视觉特征提取

局部二值模式（LBP）

特征变换

对已有向量特征进行变换，得到新特征的过程。

维数缩减

维度灾难是指当数据的维度（特征数）过高时，模型计算复杂度高、存储开销大、距离计算变得不准确，甚至模型性能下降的问题。

缓解维数灾难：降维。通过维数缩减，可以将原始高维空间的数据投影到一个低维子空间中。

• 在低维子空间里，数据的密度通常会大幅度提高。
• 数据的距离计算、分类、聚类等操作会变得更容易、更准确。

Q: 为什么能降维？

A: 在很多情况下，尽管我们采集的数据是高维的，但这些高维数据的本质特征通常只分布在低维空间内。这种现象是因为：

• 冗余特征：许多特征是高度相关的，含有重复信息。
• 任务相关特征嵌入低维空间：与学习任务密切相关的特征往往位于某个低维子空间内，而不相关的特征只会引入噪声。

通俗理解：高维数据往往有很多“水分”（冗余和噪声），通过降维可以提取出核心信息，就像将大海捞针简化为池塘捞针。

非均匀性祝福：数据在高维空间中的分布可能看起来稀疏，但实际上，它们大多集中在一个低维流形（低维嵌入空间）上。

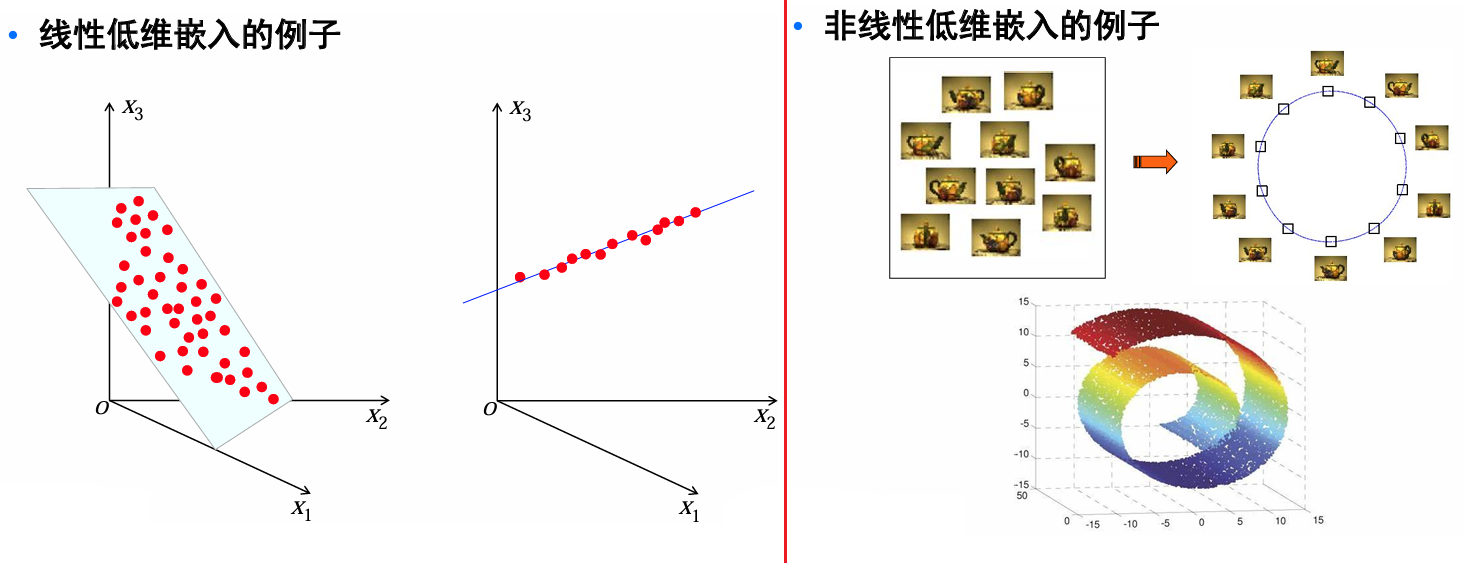
线性降维法

• 对高维空间中的样本进行线性变换：

  ，其中，，，。

• 变换矩阵可视为维空间中由个基向量组成的矩阵。

• 可视为样本与个基向量分别做内积而得到，即在新坐标系下的坐标。新空间中的特征是原空间中特征的线性组合，这就是线性降维法。

• 不同降维方法的差异：对低维子空间的性质有不同的要求，即对施加不同的约束。

PCA

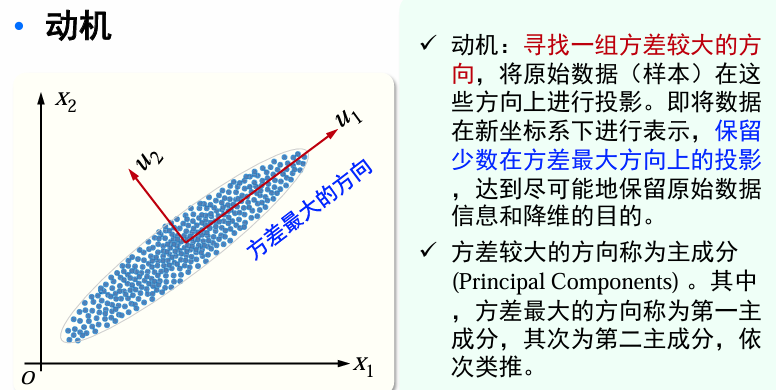
给定条件：个样本，每个样本。

目标：我们想要在投影数据中捕获最大可能的方差，即把数据从维投影到维，其中。

设是主成分，假设满足正交性：，，且，。我们只需要前个主成分。

成分	对应公式
数据点沿的投影
均值沿的投影
投影数据（沿投影方向）的方差
想要获得使投影数据方差最大化的方向

$$\begin{align} \text{var}&=\frac{1}{n}\sum_{i = 1}^{n}(w_1^Tx_i - w_1^T\overline{x})^2\\ &=\frac{1}{n}\sum_{i = 1}^{n}(w_1^Tx_i - w_1^T\overline{x})(w_1^Tx_i - w_1^T\overline{x})^T\\ &=\frac{1}{n}\sum_{i = 1}^{n}w_1^T(x_i - \overline{x})(x_i - \overline{x})^Tw_1\\ &=w_1^T\left(\frac{1}{n}\sum_{i = 1}^{n}(x_i - \overline{x})(x_i - \overline{x})^T\right)w_1\\ &=w_1^TCw_1 \end{align}$$

其中是数据的协方差矩阵。则有：

$$\max w_1^TCw_1\\ s.t.\ w_1^Tw_1 = 1$$

现在引入拉格朗日乘子到这个问题中，得到如下目标函数：

$$\text{obj}=w_1^TCw_1-\lambda(w_1^Tw_1 - 1)\\ \frac{\partial\text{obj}}{\partial w_1}=2Cw_1 - 2\lambda w_1 = 0\\ Cw_1=\lambda w_1$$

这只是一个特征值方程。因此，必须是的一个特征向量。

我们现在知道必须是的一个特征向量，是相应的特征值。但是，有多个特征向量，哪一个是呢？

考虑：

$$w_1^TCw_1 = w_1^T\lambda w_1=\lambda w_1^Tw_1=\lambda$$

我们想要最大化投影数据方差：因此应该是最大的特征值，是的第一个特征向量（具有特征值），这是第一个主成分（数据中方差最大的方向）。

若A是对称阵，此时左特征空间=右特征空间、U=V：

算法实现

步骤	公式
计算数据均值
计算数据的协方差矩阵
对矩阵进行特征值分解	取最大的个特征值对应的特征向量，组成投影矩阵
将每一个数据进行投影	，

进一步的分析

Q: 如何仅用一个超平面从整体上对所有样本进行恰当的表示？

A: 通常有如下两种思路：

• 可区分性：样本点在这个超平面上的投影能够尽可能地分开。（方差最大化）
• 可重构性：样本到这个超平面的距离都足够近。（重构误差最小化）

PCA －采用最大可分性观点

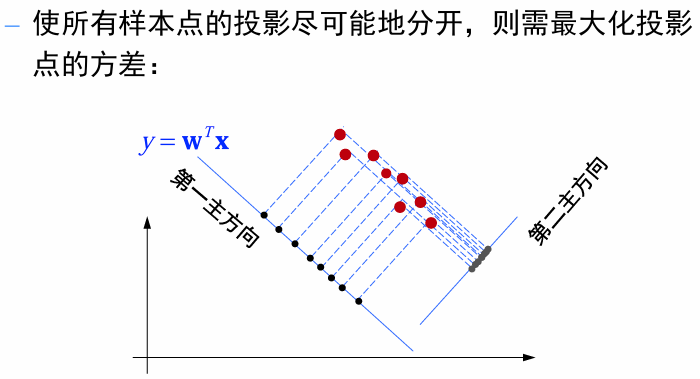
PCA——采用重构的观点

由定义新坐标系：假定投影变换是正交变换，即新坐标系由来表示（），的模等于1，与两两正交。

设样本点在新坐标系下的坐标为：

$$y_i = [y_{i1},y_{i2},\cdots,y_{id}]^T\in R^d\\ y_{ij}=w_j^Tx_i,\quad w_j\in R^m,\quad j = 1,2,\cdots,d\\ \iff y_i = W^Tx_i$$

在旧坐标系下，可得的重构表示：

$$\hat{x}_i=\sum_{j = 1}^{d}y_{ij}w_j = Wy_i,\quad i = 1,2,\cdots,n$$

重构误差：

$$\begin{align} \sum_{i = 1}^{n}\|x_i - \hat{x}_i\|^2&=\sum_{i = 1}^{n}\|x_i - Wy_i\|^2\\ &=\sum_{i = 1}^{n}((Wy_i)^TWy_i - 2x_i^TWy_i + x_i^Tx_i)\\ (\because W^TW = I)&=\sum_{i = 1}^{n}(y_i^Ty_i - 2y_i^Ty_i + x_i^Tx_i)\\ (\because y_i = W^Tx_i)&=-\sum_{i = 1}^{n}y_i^Ty_i+\text{const}=-\sum_{i = 1}^{n}(W^Tx_i)^T(W^Tx_i)+\text{const}\\ &=-\text{tr}\left(\sum_{i = 1}^{n}(W^Tx_i)^T(W^Tx_i)\right)+\text{const}\\ (\because \text{tr}(AB)=\text{tr}(BA))&=-\text{tr}\left(W^T\sum_{i = 1}^{n}x_ix_i^TW\right)+\text{const}\\ (\because tr(A)+tr(B)=tr(A+B)) \end{align}$$

令:

$$\begin{align} \sum_{i = 1}^{n}\|x_i - \hat{x}_i\|^2&=tr(W^T\sum_{i = 1}^{n}x_ix_i^TW)+\text{const}\\ &=-\text{tr}\left(W^TXX^TW\right)+\text{const} \end{align}$$

假定数据已经零均值化，即

$$XX^T=\sum_{i = 1}^{n}x_ix_i^T=\sum_{i = 1}^{n}(x_i - \overline{x})(x_i - \overline{x})^T=nC$$

于是，获得主成分分析的最优化模型：

$$\max_{W\in R^{m\times d}}\text{tr}(W^TCW)=\sum_{i = 1}^{d}w_i^TCw_i\\ s.t.\ W^TW = I$$

讨论：

• 降低至多少维：（比如，）
  • 也可以采用交叉验证，结合最近邻分类器来选择合适的维度。
• 舍弃个特征值对应的特征向量导致了维数缩减。
  • 舍弃这些信息之后能使样本的采样密度增大，这正是降维的重要动机。
  • 另外，当数据受到噪声影响时，最小的特征值所对应的特征向量往往与噪声有关，将它们舍弃可在一定程度上起到去噪的效果。

LDA

线性判别分析（Linear Discriminant Analysis，LDA）是一种经典的线性判别学习方法。

算法思想：对于两类分类问题，给定训练集，设法将样本投影到一条直线上，使得同类样本的投影点尽可能接近，不同类样本的投影点尽可能相互远离。对新样本分类时，将其投影到这条直线上，再根据投影点的位置来判断其类别。

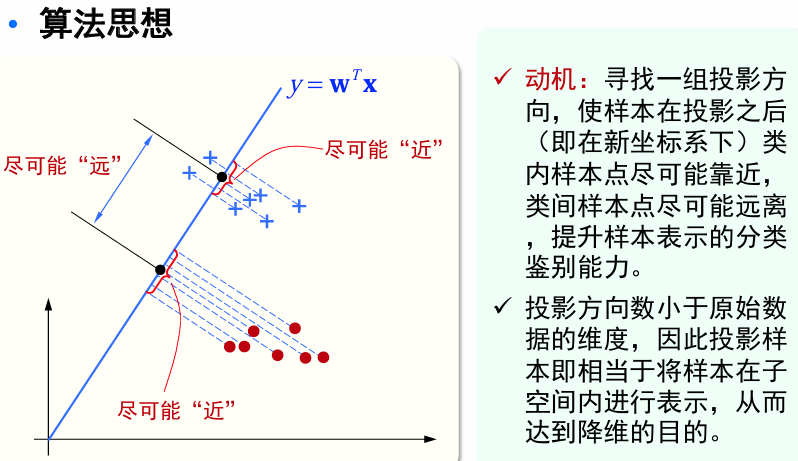
样本集，，令、、分别表示第类的样本集合、均值向量、协方差矩阵。

若将数据投影到方向上，则两类样本的中心在直线上的投影分别为和；两类样本的协方差分别为和。

• 欲使同类样本的投影点尽可能接近，可让同类样本投影点的方差尽可能小，即尽可能小。

• 欲使异类样本的投影点尽可能远离，可让类中心点之间的距离尽可能大，即尽可能大。

最大化如下目标函数：

$$J=\frac{\|w^T\mu_0 - w^T\mu_1\|^2_2}{w^T\Sigma_0w + w^T\Sigma_1w}\\ =\frac{(u_0-u_1)^Tww^T(u_0-u_1)}{w^T(\Sigma_0+\Sigma_1)w}\\ =\frac{w^T(\mu_0 - \mu_1)(\mu_0 - \mu_1)^Tw}{w^T(\Sigma_0+\Sigma_1)w}$$

主要因为得到的数，所以才可以交换。分子使两个类的中心距离尽可能远；分母使两类的类内方差尽可能小。

定义矩阵形式：

类内散度矩阵	类间散度矩阵

目标函数重写为（广义Rayleigh商）：

$$J=\frac{w^T S_b w}{w^T S_w w}$$

注意：的值与向量的长度无关，只与其方向有关，不失一般性可令为单位长度的向量。

由于目标函数值与长度无关（只与方向有关），因此可采用一种更直观的方法：令：

$$\max w^T S_b w,\quad s.t.\quad w^T S_w w = 1$$

根据拉格朗日乘子法，于是有：

$$S_b w=\lambda S_w w\Rightarrow S_w^{-1}S_b w=\lambda w$$

上式表明：为是矩阵的特征向量。

构造性求解方法 :

$$S_b=(\mu_0 - \mu_1)(\mu_0 - \mu_1)^T\\ S_b w=(\mu_0 - \mu_1)(\mu_0 - \mu_1)^T w=s\cdot(\mu_0 - \mu_1),\quad s = (\mu_0 - \mu_1)^T w\in R$$

上式表明：方向与的方向相同。不妨令:

我有想：为什么可以等价于?

但想了一下，假使就可以了。

$$S_b w=\lambda(\mu_0 - \mu_1)\\ \because S_b w=\lambda S_w w\\ w = S_w^{-1}(\mu_0 - \mu_1)$$

所以最终的结果就是得到投影：

投影后，可以对两类数据进行分类：

多类LDA算法(设类别数为c)

相关矩阵定义

• 全局散度矩阵：

  $$S_t=\sum_{i = 1}^{n}(x_i - \mu)(x_i - \mu)^T,\quad \mu=\frac{1}{n}\sum_{i = 1}^{n}x_i$$

• 类内散度矩阵：

  $$S_w=\sum_{j = 1}^{c}S_{wj},\quad S_{wj}=\sum_{x\in X_j}(x - \mu_j)(x - \mu_j)^T,\quad \mu_j=\frac{1}{n_j}\sum_{x\in X_j}x$$

• 类间散度矩阵：

  $$S_b = S_t - S_w=\sum_{j = 1}^{c}n_j(\mu_j - \mu)(\mu_j - \mu)^T$$

其中，为属于第类的样本个数。

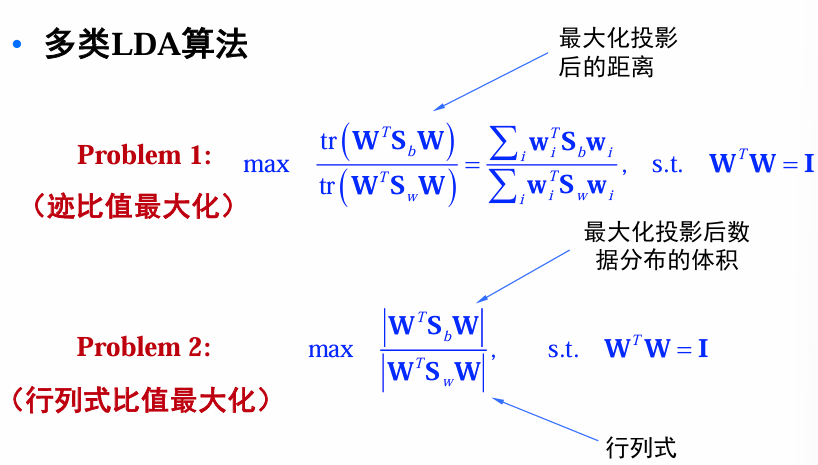
Problem 1与Problem 2的解是不同的，Problem 2的解可以通过求解如下广义特征值问题得到; Problem 1的求解较复杂【略】

局部线性判别分析

LDA局限性

• LDA假设数据是高斯分布的，这在很多真实数据中不一定成立。
• LDA希望类间距离大（分类区分性高），同时使 类内距离小（紧凑性强）。但对于复杂的、高维数据，这种方法可能无法捕捉到数据的局部结构，导致投影结果并不能有效区分类别。

局部线性判别分析旨在克服LDA的局限性，主要考虑数据的局部几何结构，即通过局部近邻关系，改善分类能力和特征提取效果。

核心思想： 修改LDA中的类内散度矩阵和类间散度矩阵，引入局部近邻约束或加权机制来更准确地描述数据的分布。

$$S_w=\sum_{y_i = y_j,x_j\in N(x_i),x_i\in N(x_j)}(x_i - x_j)(x_i - x_j)^T\\ S_b=\sum_{y_i\neq y_j,x_j\in N(x_i),x_i\in N(x_j)}(x_i - x_j)(x_i - x_j)^T$$

局部分析技术

• Neighborhood constraints（方法一,近邻判别分析）
• Locally weighting（方法二,局部Fisher判别分析）
  • Weighting for 1 - NN
  • Local Fisher discriminant analysis

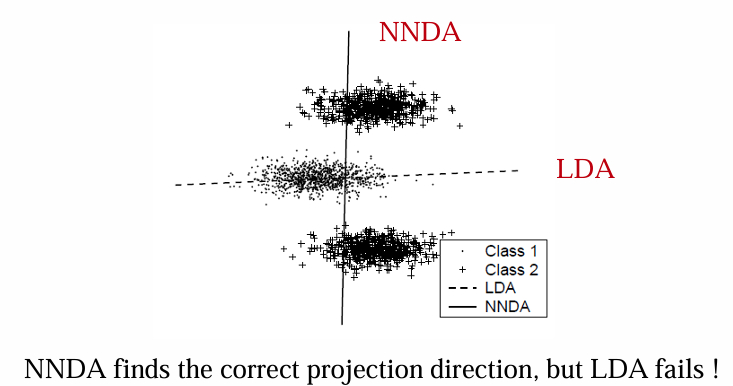
近邻判别分析（NNDA）

近邻约束中的一个问题是近邻数的选择。

此图展示了两类最近邻加权的示意图，分别用浅蓝色和紫色表示不同类别的数据点，和是不同类中的数据点，和是距离。

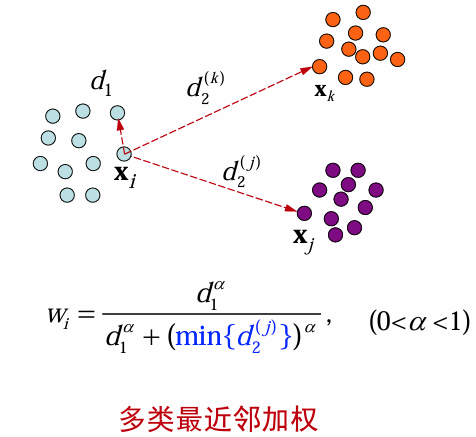
展示了多类最近邻加权的示意图，分别用浅蓝色、橙色和紫色表示不同类别的数据点，和是不同类中的数据点，和是距离。

对相关矩阵修改：

• 类内散度矩阵： $$S_w=\sum_{y_i = y_j,x_j\in N_{I - nn}(x_i),i = 1,2,\cdots,n}W_{i}(x_i - x_j)(x_i - x_j)^T$$
• 类间散度矩阵： $$S_b=\sum_{y_i\neq y_j,x_j\in N_{I - nn}(x_i),i = 1,2,\cdots,n}W_{i}(x_i - x_j)(x_i - x_j)^T$$

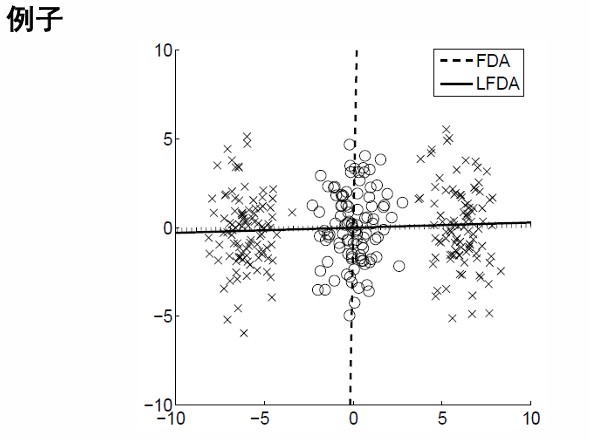
局部Fisher判别分析（LFDA）

动机:

• LFDA不强制要求同一类中相距较远的数据对接近，这样可以更好地保留数据的局部几何结构。
• 通过邻域加权机制，强调局部的关系而不是全局的特性。

构建仿射矩阵A

$$\begin{align} A&=\begin{pmatrix} A_{11} & A_{12} & \cdots & A_{1n}\\ A_{21} & A_{22} & \cdots & A_{2n}\\ \cdots & \cdots & \cdots & \cdots\\ A_{n1} & A_{n2} & \cdots & A_{nn} \end{pmatrix}\\ A_{ij}&=\begin{cases} 1, & \text{if } x_j \text{ is a neighbor of } x_i\\ 0, & \text{otherwise} \end{cases}\\ \text{or}\ A_{ij}&=\begin{cases} \exp(-\left\|x_j - x_i\right\|^2/(2\sigma^2)), & \text{if } x_j \text{ is a neighbor of } x_i\\ 0, & \text{otherwise} \end{cases} \end{align}$$

修改相关矩阵：

• 类内散度矩阵

  $$S_w=\frac{1}{2}\sum_{i,j}\overline{A}_{ij}^{(w)}(x_i - x_j)(x_i - x_j)^T\\ \overline{A}_{ij}^{(w)}=\begin{cases} A_{ij}/n_c, & \text{if } y_i = y_j = c\\ 0, & \text{if } y_i\neq y_j \end{cases}$$

• 类间散度矩阵

  $$S_b=\frac{1}{2}\sum_{i,j = 1}^{n}\overline{A}_{ij}^{(b)}(x_i - x_j)(x_i - x_j)^T\\ \overline{A}_{ij}^{(b)}=\begin{cases} A_{ij}(1/n - 1/n_c), & \text{if } y_i= y_j = c\\ 1/n, & \text{if } y_i \neq y_j \end{cases}$$

特征选择

特征变化和特征选择是处理高维数据的两大主流技术。

任务：给定一个学习任务、对于给定的特征数据特征集，从中选出与任务相关(对学习任务有利)的特征子集。

目的：降维、去除冗余、选择与任务相关的特征。

评价准则

“理想”评价准则：对分类任务，评价准则反映在一组特征下，第类和第类的可分尺度。

基于距离的评价准则

记和分别为类别和的两个样本。记两者之间的距离为：。

定义所有类别上的总距离为：

$$J_d(x)=\frac{1}{2}\sum_{i = 1}^{c}\sum_{j = 1}^{c}P_iP_j\sum_{k = 1}^{n_i}\sum_{l = 1}^{n_j}d(x_i^{(k)},x_j^{(l)})$$

其中，：第类的先验概率；：第类的样本数。

若采用平方欧氏距离：，则有：

$$J_d(x)=\sum_{i = 1}^{c}P_i\left[\frac{1}{n_i}\sum_{k = 1}^{n_i}(x_i^{(k)} - m_i)^T(x_i^{(k)} - m_i)+(m - m_i)^T(m - m_i)\right]$$

其中，：第类的中心；：所有数据点的中心。

利用散度矩阵，可将上式整理成更简单的形式。

定义类间/类内散度如下：

$$S_b=\sum_{i = 1}^{c}P_i(m_i - m)(m_i - m)^T\\ S_w=\sum_{i = 1}^{c}P_i\frac{1}{n_i}\sum_{k = 1}^{n_i}(x_i^{(k)} - m_i)(x_i^{(k)} - m_i)^T\\ J_d(x)=\text{tr}(S_b + S_w)$$

特别地，上述计算可以定义在任何特征子集上！

类似于线性判别准则，可定义如下的评价准则，其核心思想是使类内散度尽可能小，类间、散度尽可能大。常用的5个判据：

$$\begin{align} J_1(x)&=\text{tr}(S_b + S_w)\\ J_2(x)&=\text{tr}(S_w^{-1}S_b)\\ J_3(x)&=\frac{\text{tr}(S_b)}{\text{tr}(S_w)}\\ J_4(x)&=\frac{\vert S_b\vert}{\vert S_w\vert}\\ J_5(x)&=\frac{\vert S_b + S_w\vert}{\vert S_w\vert} \end{align}$$

基于分布的评价准则：基于类条件概率密度函数

假设定义了基于类条件概率密度函数和之间的一个“距离”函数：

• 该“距离”函数应该是非负的；

• 该距离应反映这两个条件分布之间的重合程度；

  • 当这两个条件分布不重叠时，该距离函数取得最大值；

  • 当这两个条件分布一样时，该距离函数应该取零值。

定义点处的对数似然比：

$$L_{ij}(x)=\ln\frac{p(x|\omega_i)}{p(x|\omega_j)}$$

KL散度：也称为相对熵(relative entropy)，定义为对数似然比的数学期望：

$$KL_{ij}\triangleq E[L_{ij}(x)]=\int p(x|\omega_i)\ln\frac{p(x|\omega_i)}{p(x|\omega_j)}dx$$

注意，KL散度不是一个度量：。可将其变成一个度量：

$$J_{ij}=KL_{ij}+KL_{ji}=\int\left[p(x|\omega_i)-p(x|\omega_j)\right]\ln\frac{p(x|\omega_i)}{p(x|\omega_j)}dx$$

基于熵的评价准则：基于类后验概率分布

后验概率反映特征刻画类别的有效性。

两个极端例子：

• 如果后验概率对于所有的类别都一样，即，则说明该特征对类别没有任何鉴别性；
• 如果后验概率对于类别为，对其他类别均为，即，则说明特征非常有效。

对于某个给定特征，样本属于各类的后验概率越平均，越不利于分类；如果越集中于某一类，则越有利于分类。因此，可利用后验概率的信息熵来度量特征对类别的可分性。

信息熵：可用来衡量一个随机事件发生的不确定性，不确定越大，信息熵越大。

香农熵	平方熵

使用时要求期望：

最优特征选择方法

穷举法

从给定的个特征中，挑选出个特征，若采用穷举法，需要遍历个子集。当很大时，该方法计算量巨大。能否有更聪明的搜索方法？

分支界定法

基本思想：将所有可能的特征组合以树的形式进行表示，采用分枝定界方法对树进行搜索，使得搜索过程尽早达到最优解，而不必搜索整个树。

基本前提：特征评价准则对特征具有单调性，即特征增多时，判据值不会减少：

$$X_1\subseteq X_2\subseteq\cdots\subseteq X_m\Rightarrow J(X_1)\leq J(X_2)\leq\cdots\leq J(X_m)$$

基于KL散度和基于信息熵的评价准则满足上述要求。

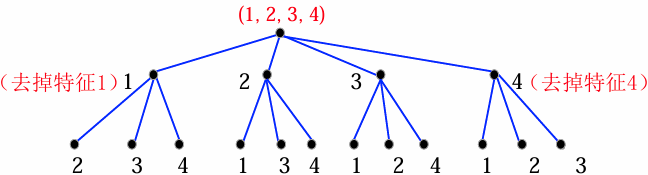
特征子集的树表示

• 根节点包含全部特征；
• 每一个节点，在父节点基础上去掉一个特征，并将去掉的特征序号写在节点的旁边；
• 对维特征，若选择个特征，每一级去掉一个特征，则需要层达到所需特征数量，即树的深度为。()

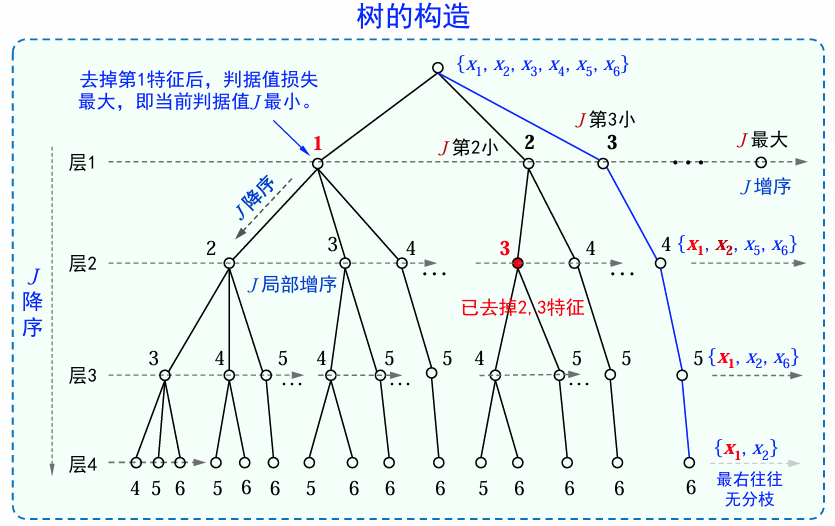
树的生长过程（树的构造）

1. 将所有特征组成根节点，根节点记为第0层；

2. 对于第1层，分别计算“去掉上一层节点单个特征后”剩余特征的评价判据值，按判据值从小到大进行排序，按从左到右的顺序生成第1层的节点；

3. 对于第2层，针对上一层最右侧的节点开始，重复第2步；

4. 依次类推，直到第层，到达叶子节点，记录对应的判据值，同时记录对应的特征选择集合。

回溯：从第一个叶子结点开始，对树进行回溯

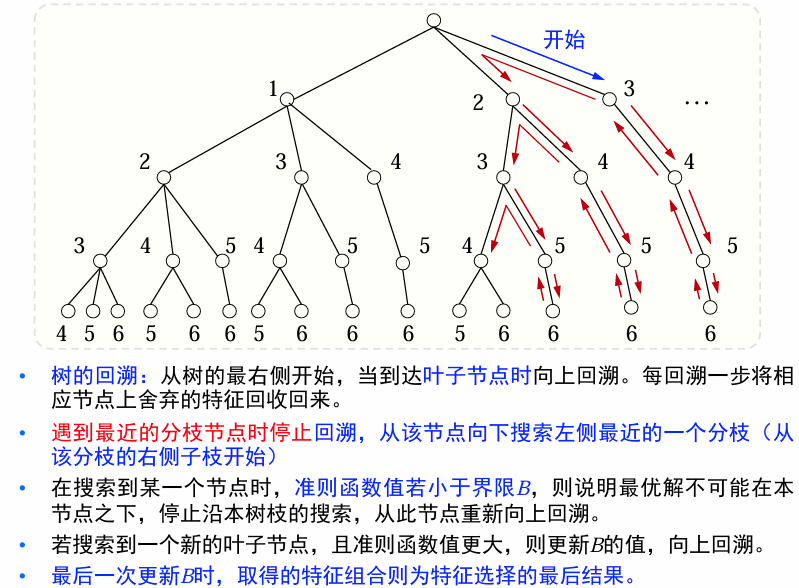
树的回溯的总体思路：对树搜索时进行分枝限界，从右到左、从上到下

特征选择的次优方法

过滤式选择方法

基本思想：过滤式方法先对数据集进行特征选择，再训练分类器。

核心任务：如何定义特征的评价准则和搜索策略

算法特点：

• 特征选择过程与后续学习器无关；
• 启发式特征选择方法，无法获得最优子集；
• 与包裹式选择方法相比，计算量降低了

单独特征选择：Relief方法

假设：特征相互独立，子集性能=包含各特征性能之和。

二分类：

对于样本:

• 猜中近邻(nearest-hit): 其同类样本中的最近邻
• 猜错近邻(nearest-miss): 其不同类样本中的最近邻

特征性能判据：

多分类

包裹式特征选择方法

过滤式特征选择方法	包裹式特征选择方法
先对数据集进行特征选择，然后再训练分类器	对给定分类方法，选择最有利于提升分类性能的特征子集
特征选择过程与分类单独进行，特征选择评价判据间接反应分类性能	特征选择过程与分类性能相结合，特征评价判据为分类器性能

• 通常采用交叉验证来评价选取的特征子集的好坏。
• 折交叉验证(-fold cross validation)，留一法(Leave - one - out)
• 包裹式特征选择方法对分类器的基本要求：
  • 分类器能够处理高维特征向量；
  • 特征维度很高、样本个数较少时，分类器依然可以取得较好的效果。

主要方法

• 直观方法：给定特征子集，训练分类器模型，以分类器错误率为特征性能判据，进行特征选择。
  • 需要大量尝试不同的特征组合，计算量大。
• 替代方法(递归策略)：首先利用所有的特征进行分类器训练，然后考查各个特征在分类器中的贡献，逐步剔除贡献小的特征。
  • 递归支持向量机（R - SVM：Recursive SVM）
  • 支持向量机递归特征剔除（SVM - RFE）
  • Adaboost

嵌入式特征选择—基于范数的特征选择

基本思路：在学习 w 的时候，对 w 进行限制，使其不仅能满足训练样本的误差要求，同时使得 w 中非零元素尽可能少（只使用少数特征）。

总结

特征选择的一般技术路线

1. 确定特征子集
2. 评价特征子集性能

评价特征子集性能常用的可分性判据

• 基于类内类间距离的可分性判据
• 基于熵的可分性判据
• 基于SVM模型的可分性判据

确定特征选择子集的方法

• 基于树的方法（最优算法）：基于分枝限界技术对特征子集的树表示进行遍历，只需要查找一小部分特征组合，即可找到全局最优的特征组合
• 遍历法（次优算法）：顺序前向法、顺序后向法、增减r法
• 稀疏约束

根据特征选择与分类器的结合程度

• 过滤式特征选择方法：“选择”与“学习”独立
• 包裹式特征选择方法：“选择”依赖“学习”
• 嵌入式特征选择方法：“选择”与“学习”同时进行