模式识别-Ch5-线性判别函数

Ch5 线性判别函数

[TOC]

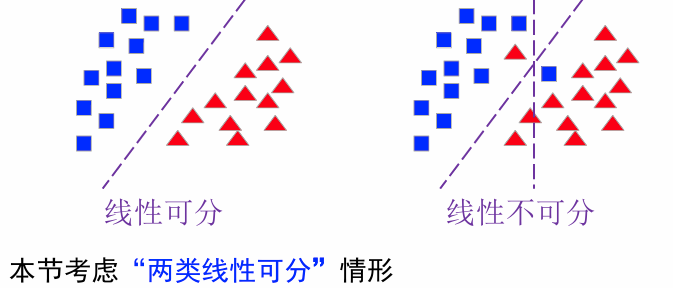
引言：生成模型 vs判别模型

生成模型 vs 判别模型

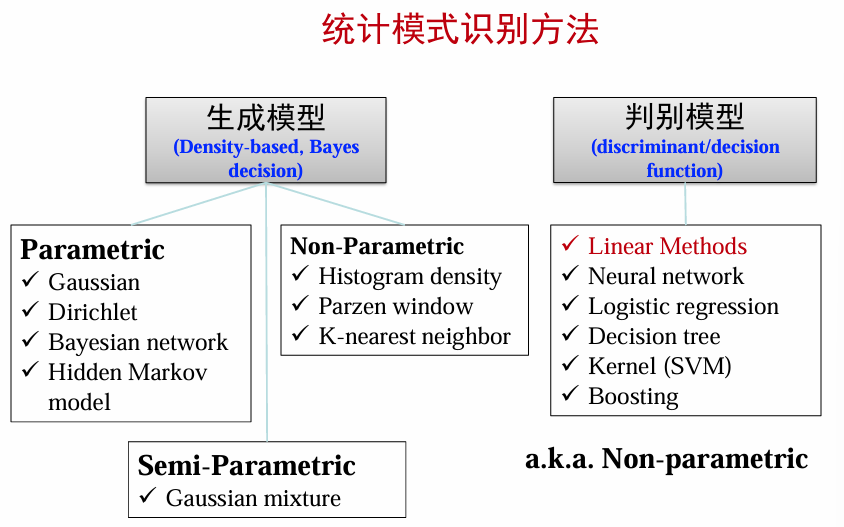
在分类问题中，生成模型和判别模型是两种不同的建模方法：

生成模型	判别模型
直接建模类条件概率或联合分布	直接建模后验概率 或决策边界
通过贝叶斯公式计算后验概率	不需要假设数据的分布形式，直接关注分类任务
示例：朴素贝叶斯、隐马尔可夫模型（HMM）	示例：支持向量机、线性判别分析、神经网络
适用于需要生成数据的场景（例如语音识别、自然语言处理）	适合直接分类任务，通常分类性能较好

判别模型分类

判别模型根据复杂性和数据分布特点，可以分为以下几类：

线性判别函数	广义线性判别函数	非线性模型	非参数模型
假设数据是线性可分的，构造一个超平面来划分不同类别。	将数据映射到高维空间，使非线性问题变成线性问题。	不依赖数据的线性假设，适合处理复杂分布的数据。	不假设数据的分布形式。
简单、高效，适合高维空间。	使用核函数（kernel function）来处理非线性分布。	学习能力强，但计算复杂度较高。	分类直接依赖于训练样本，适合小样本场景。
感知器、支持向量机、Fisher线性判别函数	核学习机	神经网络、决策树	K近邻分类、高斯过程

假设有n个d维空间中的样本，每个样本的类别标签已知，且一共有c个不同的类别。

• 学习问题：假定判别函数的形式已知，采用样本来估计判别函数的参数。
• 推理、预测问题：对于给定的新样本，用判别函数判定属于中的哪个类别。

	c>2(one-vs-all)	c=2
判别函数	每个类别对于判别函数, 用于区分第 类和其他个类，其数值表示 属于第 类的概率、置信度、打分等.
决策准则	: 被分为类	: 分为第一类

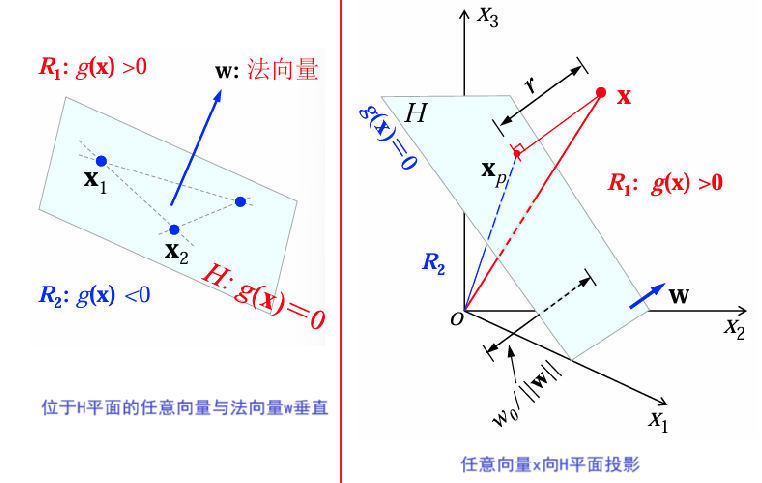
线性判别函数与决策面

线性判别函数

线性判别函数定义为：

$$g(x) = \sum_{i=1}^d w_i x_i + w_0 = w^T x + w_0$$

• ：权重向量，决定分类超平面的方向。
• ：偏移量（阈值），决定超平面的位置。

两类情况下的决策

决策依据判别函数 的符号：

$$\begin{cases} x \in \omega_1, & \text{if } g(x) > 0 \\ x \in \omega_2, & \text{if } g(x) < 0 \\ \text{uncertain}, & \text{if } g(x) = 0 \end{cases}$$

两类问题中的决策面:

• ：，用于将特征空间分为两类区域：

• ：

• ：

超平面的法向量为 ，垂直于决策面。

• 对于位于 内的任意向量，其法向量满足：

• 对于任意样本/向量，将其向决策面内投影，并写成两个向量之和：

  $$x=x_p+r\frac{w}{\|w\|}$$

  是在超平面上的投影，是点到超平面的代数距离。若.

多类问题下决策

在多类分类问题中，通常使用多个二分类器来解决问题。常见策略有：

一对多（One-vs-All）	一对一（One-vs-One）	多对多
每个类别与其余类别分别构造一个二分类器，共需构造 c 个二分类器。	每两个类别配对构造一个二分类器，共需构造 个二分类器。	—-
预测时：若只有一个分类器的预测为正，其对应类别即为预测结果；若多个分类器的预测为正，则需要比较判别函数值。	预测时, 对测试样本使用投票法，预测得票最多的类别。	使用纠错编码（Error Correcting Output Codes, ECOC），实现层次化分类。

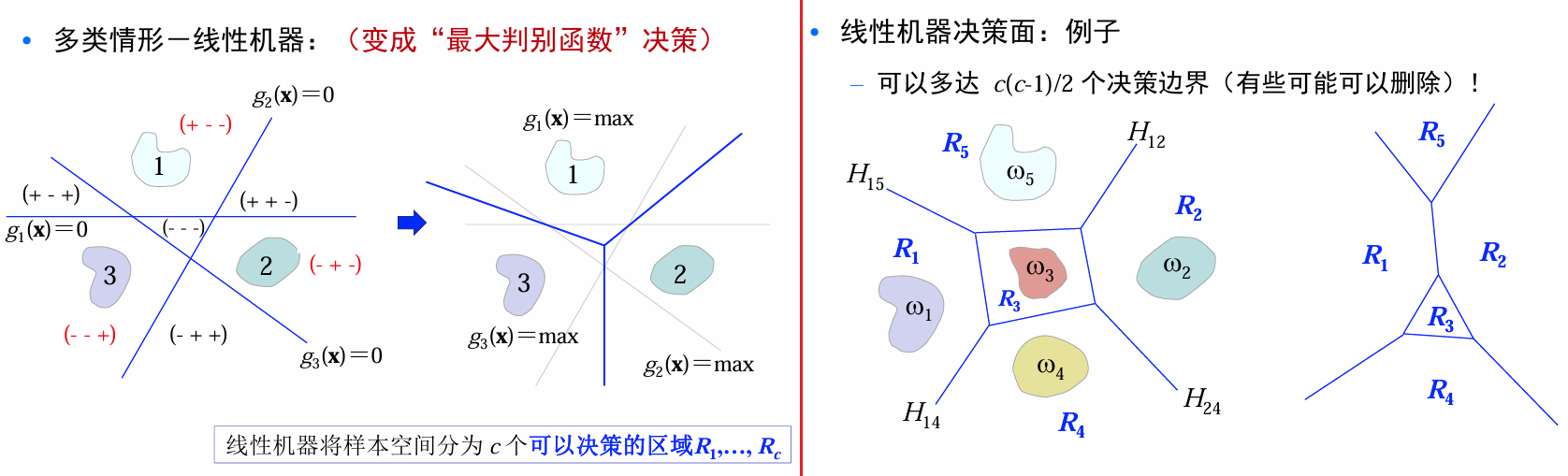
多类情形-线性机器

因为不使用判别函数的函数值、仅仅使用决策面进行分类，one-vs-all\one-vs-one都有可能存在不确定区域。

• 考虑one - vs - all情形，构建个两类线性分类器：

  $$g_i(x)=W_i^T x + w_{i0},\quad i = 1,2,\cdots,c$$

• 对样本，可以采用如下决策规则（最大判别函数决策）：

  • 对，如果，则被分为类；否则不决策

  • $$g_i(x)=\max_{j = 1,2,\cdots,c}g_j(x)\Rightarrow x\in\omega_i$$

  • 线性机器将样本空间分为个可以决策的区域。

线性决策面优缺点

• 所有的决策区域都是凸的——便于分析
• 所有的决策区域都是单连通的——便于分析

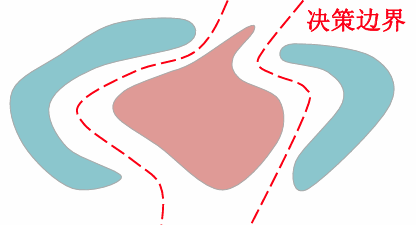
• 凸决策区域：限制分类器的灵活性和精度
• 单连通区域：不利于复杂分布数据的分类（比如：分离的多模式分布）

广义线性判别函数

将原来的数据点 x通过一种适当的非线性映射将其映射为新的数据点 y, 从而在新的特征空间内应用线性判别函数方法。

例：二次判别函数

二次判别函数形式：

$$g(x)=w_0+\sum_{i = 1}^{d}w_i x_i+\sum_{i = 1}^{d}\sum_{j = 1}^{d}w_{ij}x_i x_j$$

其中共有个系数待估计（），且为决策面，它是一个二次超曲面。

定义如下非线性变换，把从维变到维：

$$y_1(x)=1\\y_2(x)=x_1\\ y_3(x)=x_2\\\dots\\y_{d + 1}(x)=x_d\\y_{d + 2}(x)=x_1^2\\y_{d + 3}(x)=x_1 x_2\\\dots\\y_{\frac{(d + 1)(d + 2)}{2}}(x)=x_d^2$$

则有：

$$\begin{align}g(x)&=w_0+\sum_{i = 1}^{d}w_i x_i+\sum^d_{i=1}\sum^d_{j=1}w_{ij}x_ix_j\\ &=\sum^{\hat d}_{i=1}a_iy_i(x) \end{align}$$

是变换函数、令，，可简写为：

$$g(x)=a^T y(x)$$

其中：

• 为广义权重向量，是经由所变成的新数据点。
• 广义判别函数对而言是非线性的，对是线性的。
• 对是齐次的，意味着决策面通过新空间的坐标原点。且任意点到决策面的代数距离为。
• 当新空间的维数足够高时，可以逼近任意判别函数。
• 但是，新空间的维数远远高于原始空间的维数时，会造成维数灾难问题。

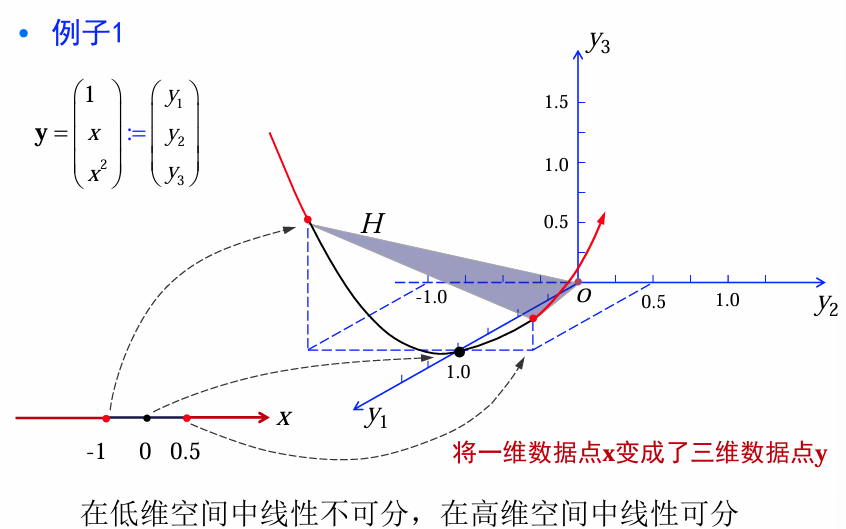
例1: 1-D判别函数

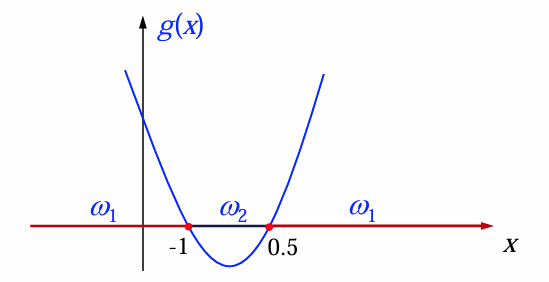
设有一维样本空间，我们期望如果或者，则属于类；如果，则属于类，请设计一个判别函数。

判别函数：

$$\begin{align} g(x)&=(x - 0.5)(x + 1)\\ &=-0.5+0.5x+x^2 \\ &=a_1+a_2x+a_3x^2 \end{align}$$

决策规则：

$$g(x)>0,x\in\omega_1\\g(x)<0,x\in\omega_2$$

映射关系：

$$y=\begin{pmatrix}1\\x\\x^2\end{pmatrix}:=\begin{pmatrix}y_1\\y_2\\y_3\end{pmatrix}$$

感知准则函数

概念

线性可分性：来自两个类别的n个样本(齐次增广表示)。存在一个权向量，对所有，均有;对所有，均有。

齐次增广->规范化增广

样本规范化：如果样本集是线性可分的，那么将属于的所有样本由变成，对所有样本，将得到。这样训练中就不需要考虑原来的样本类别。

规范化增广样本：1.将所有样本写成齐次增广形式；2.属于的所有样本由变成

解向量与解区

解向量：线性可分的情况下，满足的权向量.

解向量 是我们需要找到的“分类方向”，它保证所有样本点都在它的正确一侧。

解区：权向量属于权空间中的一点，每个样本对的位置均起到限制作用()

• 任何一个样本点均可以确定一个超平面(是法向量，所有与垂直的属于，且决定了超平面的方向。)
• 如果解向量存在，那必在每个超平面的正侧(); 个样本将产生个超平面。每个超平面将空间一分为二。解向量存在于所有超平面正面的交集区域，此区域内的任意向量都是解向量。

限制解区：解向量存在的话，通常不唯一。根据经验越靠近区域中间的解向量，越能对新的样本正确分类，所以引入附加条件来限制解空间。

• way1: 寻找单位长度的解向量，最大化样本到分界面的最小距离。

• way2: , 寻找满足的最小长度的解向量, b:margin.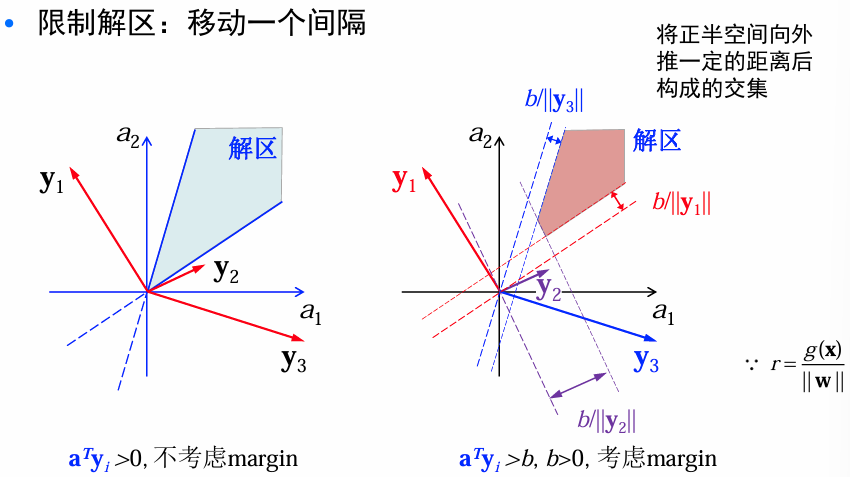

  

感知准则函数

现在考虑构造解线性不等式的准则函数问题。令维被错分的样本数。但这个函数是分段常数函数，对梯度搜索不友好。因此考虑感知器准则函数：

$$J_p(a)=\sum_{y\in \mathcal{Y}}(-a^Ty)$$

是错分样本集合。

当被错分：，使.

在可分情况下，当且仅当是空集时将=0，此时不存在错分样本。

目标：

梯度下降更新：是当前迭代的结果，是前一次迭代的结果，是被 错分的样本集合 ，为步长因子（更新动力因子，学习率）。

$$\frac{\partial J_p(a)}{\partial a}=-\sum_{y\in\mathcal{Y}}y\\ a_{k+1}=a_k-\eta_k\frac{\partial J_p(a)}{\partial a}\vert_{a=a_k}=a_k+\eta_k\sum_{y\in \mathcal{Y}_k}y$$

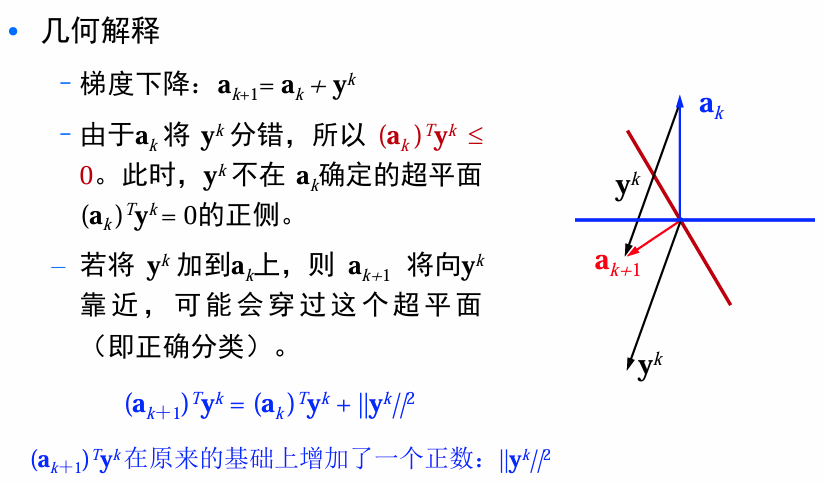
算法收敛性

以固定增量单样本修正方法为例来说明算法的收敛性：

对于权向量 ，如果错分某样本，则将得到一次修正。由于在分错样本时 才得到修正，不妨假定只考虑由错分样本组成的序列。即每次都只需利用一个分错样本来更正权向量。

记错分样本序列为 。考虑此情形的算法收敛性问题。

收敛性定理：在样本线性可分的情形下，固定增量单样本权向量修正方法收敛，并可得到一个可行解。

证明思路：设是一个解向量，只需证明即可。

• 算法每次迭代都会使权向量到解向量的距离减少1个常数C
• 假设,则dst在经过C次迭代后(计算了足够长的步数)，算法收敛。

感觉证明不考，因此略。

松驰方法

学习准则

在感知函数准则中，目标函数中采用了 的形式。实际上有很多其它准则也可以用于感知函数的学习。

线性准则	平方准则	松驰准则
		$J_r(a)=\frac 1 2\sum_{y\in\mathcal{Y}}(a^Ty-b)^2/\	y\	^2$
为错分样本集合	为错分样本集合	是的样本集合
分段线性，梯度不连续	梯度连续，但目标函数过于平滑，收敛速度很慢。此外，目标和拿书过于受到最长样本的影响。	避免了线性准则和平方准则的缺点。时，对所有,意味着是空集。

松弛准则的梯度下降：

$$\frac{\partial J_r(a)}{\partial a}=\sum_{y\in\mathcal{Y}}\frac{a^Ty-b}{\|y\|^2}y\\ a_{k+1}=a_k-\eta_k\sum_{y\in\mathcal{Y}}\frac{a^Ty-b}{\|y\|^2}y$$

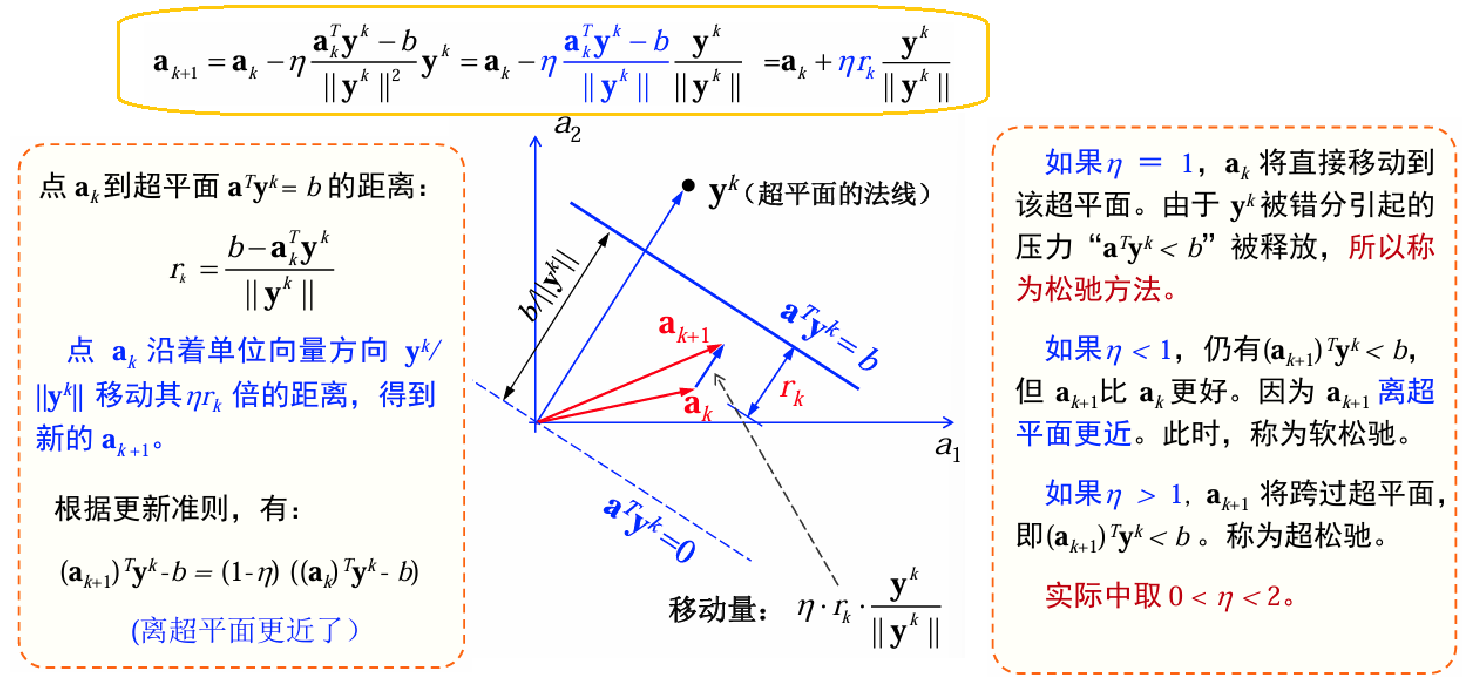
收敛性证明略。

最小平方误差（MSE）准则函数

前面考虑的准则函数都是只考虑被错分的样本。现在考虑一种包含所有样本的准则函数。

动机：对两类分问题，感知准则函数是寻找一个解向量 a，对所有样本 ，满足 。或者说，求解一个不等式组，使满足 的数目最大，从而错分样本最少。

$$a^Ty_i=b_i>0$$

其中，是任意给定的正常数，通常取，或者。其中，（或）为属于第类样本的总数，且。

线性判别函数的参数估计

可得一个线性方程组：

$$\begin{bmatrix} y_{10} & y_{11} & \cdots & y_{1d}\\ y_{20} & y_{21} & \cdots & y_{2d}\\ \vdots & \vdots & \ddots & \vdots\\ y_{n0} & y_{n1} & \cdots & y_{nd} \end{bmatrix} \begin{bmatrix} a_0\\ a_1\\ \vdots\\ a_d \end{bmatrix} = \begin{bmatrix} b_1\\ b_2\\ \vdots\\ b_n \end{bmatrix}$$

• 如果可逆，则。
• 但通常情形下，，因此，考虑定义一个误差向量：，并使误差向量最小。

平方误差准则函数

$$J_s(a)=\|e\|^2=\|Ya - b\|^2=\sum_{i = 1}^{n}(a^T Y_i - b_i)^2$$

对其求导：

$$\frac{\partial J_s(a)}{\partial a}=\sum_{i = 1}^{n}2(a^T Y_i - b_i)Y_i = 2Y^T(Ya - b)=0\\ Y^T Ya = Y^T b\Rightarrow a=(Y^T Y)^{-1}Y^T b = Y^\dagger b$$

其中，为的伪逆。

实际计算（正则化技术）：

梯度下降法

计算伪逆需要矩阵的逆，计算复杂度高。如果原始样本的维数很高，比如，将十分耗时。

• 批处理梯度下降：

  $$a_{k + 1}=a_k+\eta_k Y^T(b - Ya_k)$$

  梯度下降法得到的将收敛于一个解，该解满足方程：

  $$Y^T(b - Ya)=0$$

• 单样本梯度下降：此方法需要的计算存储量会更小（此时考虑单个样本对误差的贡献）

  $$a_{k + 1}=a_k+\eta_k(b_k-(a_k)^T y^k)y^k$$

  

  

  

Ho-Kashyap方法

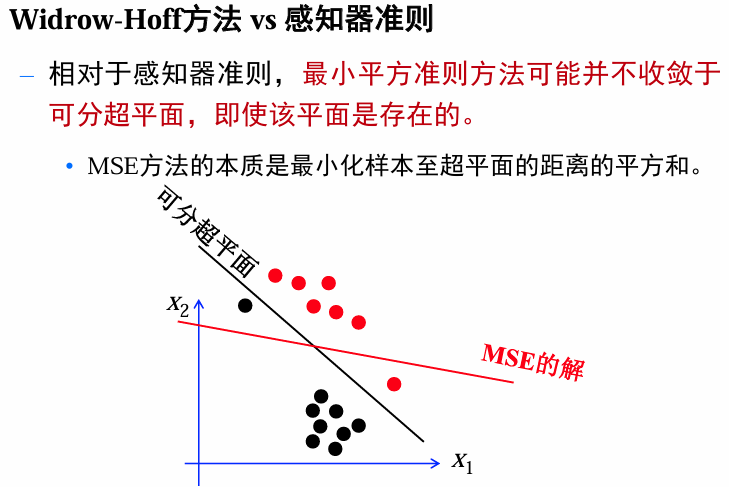
感知器和松弛法对线性可分样本集可找到分离向量，但对于不可分的情况就不收敛了。

MSE算法不管样本是否可分都能得到一个权向量，但并不能保证在可分的情况下这个向量一定是分类向量。

若margin 是任意选择的，MSE只是,所得到的最优解并不需要位于可分超平面上。若训练样本刚好是线性可分的，那么存在满足：

$$Y\hat a=\hat b>0$$

当我们设置，利用MSE，就能找到一个分类向量。但是我们没法预知。

对MSE准则函数更新为：

$$J_s(a,b)=\|Ya-b\|^2$$

ps：直接优化将导致平凡解，所以需要给添加约束条件：.

此时可以解释为margin.

梯度下降

$$\frac{\partial J_s(a,b)}{\partial a}=2Y^T(Ya-b),\quad \frac{\partial J_s(a,b)}{\partial b}=-2(Ya-b)\\ b_{k+1}=b_k-\eta_k\frac{\partial J_s(a,b)}{\partial b}$$

约束条件：,

因为,要使,可以要求:

$$b_{k+1}=b_k-\eta_k\frac12\left(\frac{\partial J_s(a,b)}{\partial b}-\vert \frac{\partial J_s(a,b)}{\partial b}\vert \right)$$

更新:

$$a_{k+1}=Y^{\dagger}b_k\\ b_1>0,\quad b_{k+1}=b_k+2\eta_ke^{\dagger}_k\\ e^{\dagger}_k=\frac 12 \left((Ya_k-b_k)+\vert Ya_k-b_k\vert\right)\Leftarrow\frac{\partial J_s(a,b)}{\partial b}=-2(Ya-b)$$

• 为了防止收敛于，可以让从一个非负向量（）开始进行更新。
• 由于要求等于，在开始迭代时可令的元素为正的分量等于零，从而加快收敛速度。

伪算法

• 由于权向量序列完全取决于，因此本质上讲Ho - Kashyap算法是一个生成margin序列的方法。
• 由于初始，且更新因子，因此总是大于。
• 对于更新因子，如果问题线性可分，则总能找到元素全为正的。
• 如果全为，此时，将不再更新，因此获得一个解。如果有一部分元素小于，则可以证明该问题不是线性可分的。(证明略)
  

多类线性判别函数

决策规则: , 被分为类。

被分为类的线性判别函数：

$$\forall j\neq i,a_i^Tx+b_i\ge a_j^Tx+b_j$$

方法一：MSE多类扩展

可以直接采用个两类分类器的组合，且这种组合具有与两类分类问题类似的代数描述形式。

线性变换(注，此处不采用规范化增广表示)：

$$z = W^T x + b,\quad W\in R^{d\times c},\quad b\in R^c$$

决策准则：

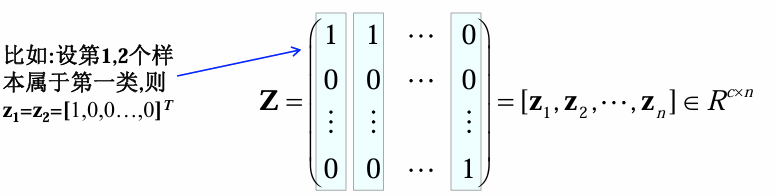
回归值的构造：one - hot编码

$$x\in\omega_j\Rightarrow z\in R^c,\quad z_{ij}=\begin{cases}1, & \text{if}\quad i = j\\0, & \text{otherwise}\end{cases}$$

若属于类，则的类别编码为一个维向量，其中第个元素为，其余为。

目标函数

$$\min_{W,b}\sum_{i = 1}^{n}\|W^T x_i + b - z_i\|_2^2$$

令：

$$W = \begin{bmatrix}W^T\\b\end{bmatrix}\in R^{(d + 1)\times c},\ \hat{x}=\begin{bmatrix}x\\1\end{bmatrix}\in R^{d + 1},\ \hat{X}=(\hat{x}_1,\hat{x}_2,\cdots,\hat{x}_n)\in R^{(d + 1)\times n}$$

则有：

$$\sum_{i = 1}^{n}\|W^T x_i + b - z_i\|_2^2=\|\hat{W}^T\hat{X}-Z\|_F^2$$

为Frobenius范数。进而有：

$$\min_{W}\|\hat{W}^T\hat{X}-Z\|_F^2\\ \hat{W}=(\hat{X}\hat{X}^T)^{-1}\hat{X}Z^T\in R^{(d + 1)\times c}\\$$

实际中：可能会遇到矩阵奇异或数值不稳定的问题。为此，我们引入正则化项（类似岭回归）

$$\hat{W}=(\hat{X}\hat{X}^T+\lambda I)^{-1}\hat{X}Z^T\in R^{(d + 1)\times c}$$

: 正则化参数，通常取一个小正数。防止过拟合以及增强数值计算的稳定性。