模式识别-Ch4-非参数估计

Ch4 非参数估计

[TOC]

参数估计方法	非参数估计方法
MLE，贝叶斯估计	Parzen窗方法、KNN
待估计的概率密度函数的形式已知，利用样本来估 计函数中的某些参数。	非参数估计方法不需要对概率密度函数的形式作任何假设，而是直接用样本估计出整个函数。

非参数密度估计

难点：选取小窗大小

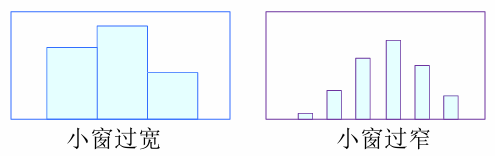
• 小窗过宽：由于假定小舱内p(x)为常数，则导致过于平均的估计结果。
• 小窗过窄：落入小舱的样本将会 很少，或者没有样本落入，从而导致对p(x)的估计不连续。

基本原理

• 给定样本集，假定这些样本是从一个服从密度函数的总体分布中独立抽取出来的，目标是给出关于的估计。
• 考虑点处的一个小区域，一个样本落入该区域概率是：

$$P = \int_{R} p(x') dx'$$

• 若个随机样本中有个样本落入小区域，是对概率的一个很好的估计（无偏估计、最大似然估计）。
  • 落入的样本数服从参数为的二项分布。
  • 当样本数越来越大时，该估计相当精确。

• 另一方面，假设连续，且小区域的体积足够小，可以假定在该小区域内是常数，则

$$P = \int_{R} p(x') dx' \approx p(x)V$$

• 于是有点处的概率密度估计:

$$p(x)V \approx \frac{k}{n} \Rightarrow p(x) \approx \frac{k}{nV}$$

收敛性

对每个样本数，都构造一个包含的小区域，从而得到一个区域序列：。令表示的体积，表示落入的样本个数。则使用个样本对点处的概率密度估计为：

$$p_n(x) = \frac{k_n}{nV_n}$$

为了使收敛到，需要满足以下三个条件：

$$\lim_{n \to \infty} V_n = 0; \quad \lim_{n \to \infty} k_n = \infty; \quad \lim_{n \to \infty} \frac{k_n}{n} = 0$$

这几个条件说明：随着样本数目的增加，小舱的体积应该尽可能小，同时又必须保证小舱内有充分多的样本，但每个小舱内的样本又必须是总数的很小一部分。

有两种常见的方法来获得满足这些条件的区域序列：

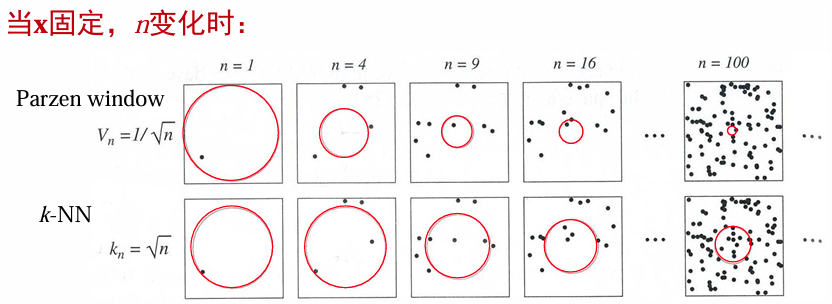
1. 指定体积作为的函数，保证收敛到。这是Parzen - window方法。（对给定的，小舱体积在全局处处保持不变，小舱内的样本数可变）
2. 指定作为的函数。这里体积是增长的，直到它包围的个邻居。这是KNN估计方法。（对给定的，小舱内的样本数不变，小舱大小可变）

这两种方法都收敛，尽管很难对它们的有限样本行为做出有意义的陈述。

-	固定，变化	固定，变化
Parzen窗	固定局部区域体积，变化
KNN	固定局部样本数，变化

Parzen窗估计

方法介绍

假设是维空间中的点，并假设小舱是一个超立方体，其棱长为，因此其体积为：

$$V_n=(h_n)^d$$

现在的任务：要统计落入以为中心的超立方体内样本的个数。为此，定义如下维单位窗函数：

$$\varphi(u)=\begin{cases} 1, & \vert u_j\vert\leq\frac{1}{2}, j = 1,2,\cdots,d\\ 0, & \text{otherwise} \end{cases} \quad (\text{here } u = [u_1,u_2,\cdots,u_d]^T\in R^d)$$

表示的每个分量都必须在的范围内。该函数在以原点为中心的维单位超立方体内取值为，而在其它地方取值均为零。

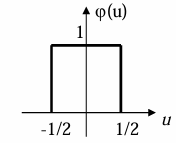
个人感觉会比较像：图像处理-傅里叶变换-冲激函数/单位脉冲。

对于点，考察样本是否在以为中心、为棱长的超立方体内，可通过如下函数来判定：

$$\varphi\left(\frac{x - x_i}{h_n}\right)$$

上式与等价(因为绝对值的存在)。

Q: 为什么使用?

A: 表示从目标点 指向样本点 的 相对位移，它是从中心 出发的方向，更符合“以 为中心”的逻辑

若共有个样本，那么落入以为中心、为棱长的超立方体内的样本总数为：

$$k_n=\varphi\left(\frac{x - x_1}{h_n}\right)+\varphi\left(\frac{x - x_2}{h_n}\right)+\cdots+\varphi\left(\frac{x - x_n}{h_n}\right)=\sum_{i = 1}^{n}\varphi\left(\frac{x - x_i}{h_n}\right)\\ p_n(x)=\frac{k_n}{nV_n}=\frac{1}{n}\sum_{i = 1}^{n}\frac{1}{V_n}\varphi\left(\frac{x - x_i}{h_n}\right)$$

是一个概率密度函数

• 定义如下函数：

  $$\delta_n(x)=\frac{1}{V_n}\varphi\left(\frac{x}{h_n}\right)\Rightarrow p_n(x)=\frac{1}{n}\sum_{i = 1}^{n}\delta_n(x - x_i)$$

• 引入如下积分变换函数：

  $$\int\delta_n(x - x_i)dx=\int\frac{1}{V_n}\varphi\left(\frac{x - x_i}{h_n}\right)dx=\frac{1}{V_n}\left|\frac{\partial x}{\partial u}\right|\int\varphi(u)du\\=\int\frac{h_n^d}{V_n}\varphi(u)du =\int\varphi(u)du = 1\\ \int p_n(x)dx = \frac{1}{n}\sum_{i = 1}^{n}1 = 1$$

窗函数的选择

确与单位脉冲 非常相似，但它是对 的“平滑近似”：

• 是 有限支持且连续的窗函数，适用于实际计算。
• 是理想化的数学工具，用于理论分析。

随着窗口宽度 逐渐缩小， 会逐渐逼近 。在概率密度估计中，我们用 来平滑地估计分布，而不是使用离散的 Dirac Delta 函数。

一般地，要保证为一个概率密度函数，只需满足：

$$\delta_n(x)\geq0,\quad\int\delta_n(x)dx = 1$$

• 反映了样本对在处概率密度估计贡献的大小，通常与到的距离有关。
• 概率密度估计就是把中所有观测样本在点的贡献进行平均。

除了以上窗函数，还可定义其它函数：

其他窗函数	公式
方窗（非单位长度）
正态窗
球窗
其中：超球体体积，：超球体半径。

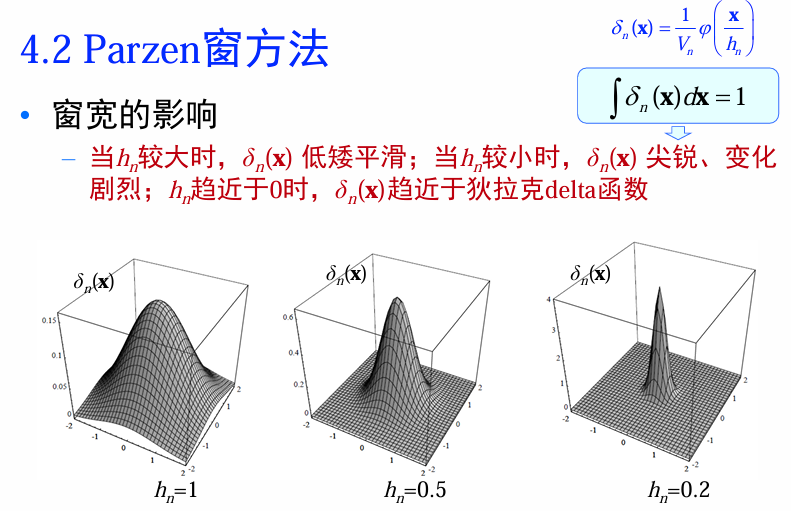
窗宽的影响

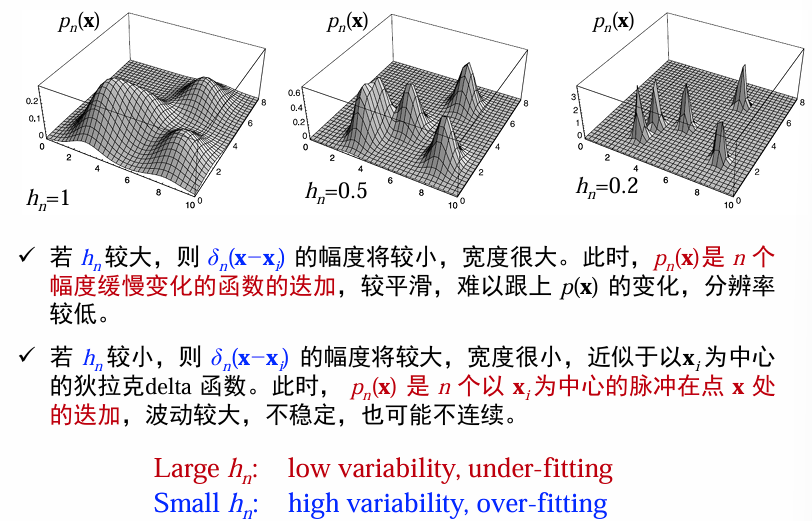
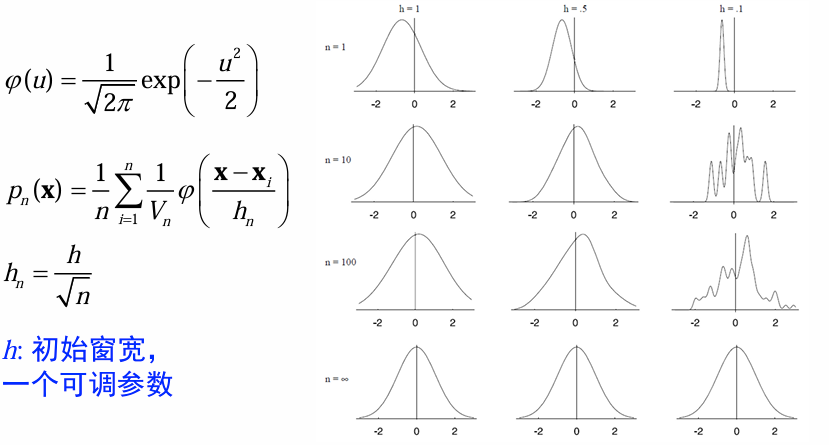
例子：用高斯窗估计高斯分布

1-D

2-D

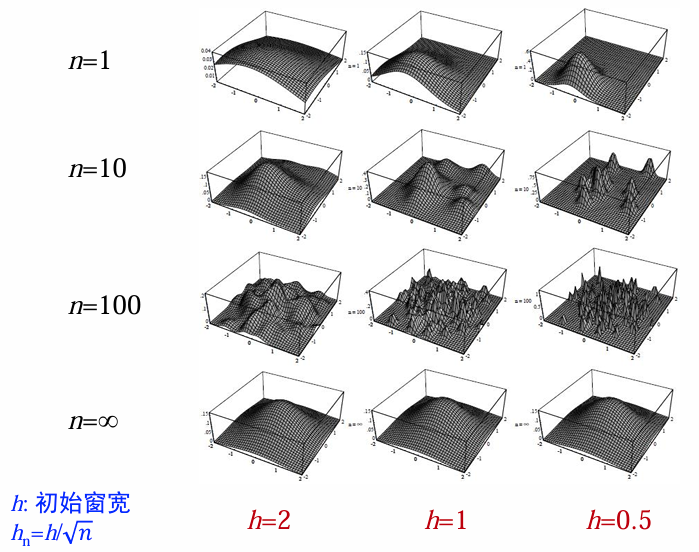
可见：使用小窗宽得到的分类界面比大窗宽的分类界面更复杂。h越大，得到的分布越平滑、h越小得到的分布越尖锐。

算法特点：

• 适用范围广，无论概率函数是规则的或者是不规则的、单峰的还是多峰的；
• 当样本数趋于无穷时，Parzen窗估计收敛于真实p(x)；
• 但该方法要求样本的数量要大；
• 选择合适的窗口函数将有利于提高估计的精度和减少样本的数量。
• 与直方图仅仅在每个固定小窗内估计平均密度不同， Parzen窗用滑动的小窗来估计每个点上的概率密度。

K近邻估计

• Parzen窗估计中，小窗的体积被视为样本个数的函数，比如。
  • 当选择得太小，导致大部分区域是空的，会使不稳定。
  • 当选择得太大，则会变得过于平坦，从而失去一些重要的空间变化。
  • 近邻估计方法是克服这一问题的一种可能方法。

基本方法

• 近邻估计是一种采用大小可变舱的密度估计方法。其基本做法是：根据总样本数确定一个参数，要求每个小舱内拥有的样本数目是。

• 在估计点处的概率密度时，我们调整包含的小舱的体积，直到小舱内恰好落入个样本，此时有：

  $$p_n(x)=\frac{k_n}{nV_n}$$

  其中不固定，与的位置相关。

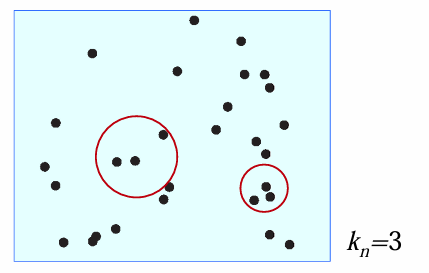
• 在密度较高的区域，窗口 会比较小，因为周围样本多，窗口不需要太大就可以包含 个样本。

  在密度较低的区域，窗口 会比较大，因为样本较稀疏，需要更大的范围来找到 个样本。

收敛性分析: 的选择对收敛的影响

$$\lim_{n \to \infty} k_n=\infty; \quad \lim_{n \to \infty} \frac{k_n}{n}=0$$

• :当样本数量 时， 应该足够大，这样才能捕捉到整体概率分布。

• : 的增长速度不能太快，否则窗口太大，局部密度信息会丢失。

点处，概率密度函数的估计值为。如果取，则

$$p_n(x)=\frac{\sqrt{n}}{nV_n}\Rightarrow p(x)\approx\frac{1}{\sqrt{n}V_n}\Rightarrow V_n\approx\frac{1}{\sqrt{n}p(x)}=\frac{V_1}{\sqrt{n}},\ V_1=\frac1{p(x)}$$

（与Parzen窗方法不同，不再是一个固定的值，而是与密度相关）

一维下解析表达式

在点处，概率密度函数的估计值为。关键是如何计算。

对于一维来讲，考虑最近邻情形，即。假定样本是点的最近邻样本，则点处的最近邻估计为：

$$p_n(x)=\frac{k_n}{nV_n}=\frac{1}{2n|x - x_1|}$$

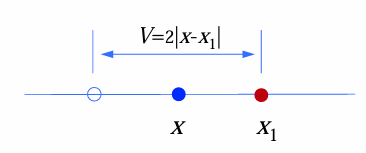
此时，近邻估计在特征空间积分为正无穷，不是严格意义的概率密度函数。

考虑近邻情形，此时：

$$p_n(x)=\frac{k_n}{nV_n}=\frac{k_n}{2n|x - x_{k_nN}|}$$

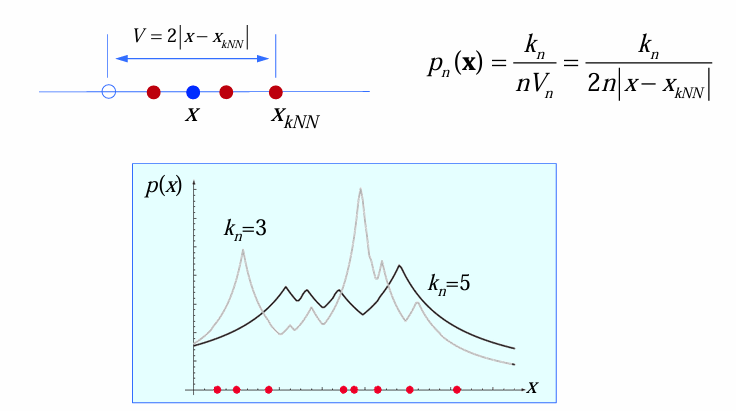
对于多维情形，可以用球来度量近邻小舱，也可以用立方体包围盒来度量近邻小舱。比如，采用立方体包围盒：

$$p_n(x)=\frac{k_n}{nV_n}=\frac{k_n}{2^d n \prod_{i = 1}^{d}|x^i - x_{k_nN}^i|}$$

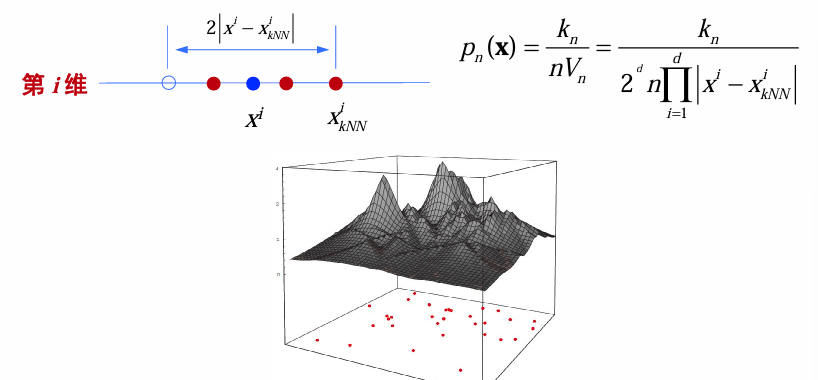
K近邻分类器

最近邻分类器

1-NN	说明
方法	对测试样本，将其与训练样本逐一进行比较，找出距离最近的训练样本，以该样本的类别作为的类别。
直观理解	给定训练样本集，对于测试样本，假设为其最近邻样本，是的类别标签。如果与充分接近，有理由相信它们的类别相同，或者类后验概率相同，即对任意类别，。
类的判别函数
决策规则

例子

现有7个二维向量：，，，，，，。假定前三个为类，后四个为类。画出最近邻法决策面。

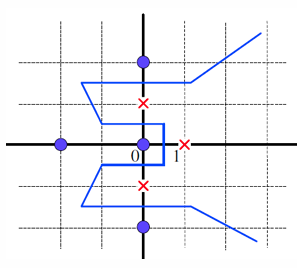
最近邻规则的错误率分析

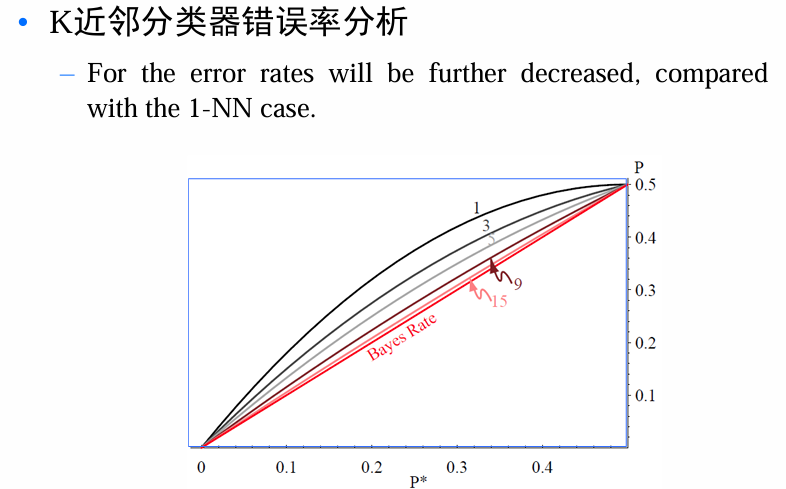
• 研究表明，在训练样本足够多时，最近邻决策可以取得很好的效果。

• 我们对最近邻规则的行为分析将针对获得无限样本条件平均错误概率，其中平均是相对于训练样本而言的。一般来说，无条件平均错误概率将通过对所有平均得到：

  $$P(e)=\int P(e|x)p(x)dx$$

• 我们应该记得贝叶斯决策规则通过对每个最小化来最小化。

• 再次回顾如果我们令$P^(e\vert x)P(e\vert x)P^P(e)$的最小可能值，那么贝叶斯错误率：

  $$P^*(e|x)=1 - P(\omega_m|x),P^*=\int P^*(e|x)p(x)dx\\ \omega_m=\arg\max_i P(\omega_i|x_i)$$

评估最近邻规则的平均错误概率: 特别地，如果是 - 样本错误率，并且如果我们定义:

$$P(e)=\lim_{n\rightarrow\infty}P_n(e)$$

那么，我们有:

$$P^*\leq P(e)\leq P^*\left(2 - \frac{c}{c - 1}P^*\right)$$

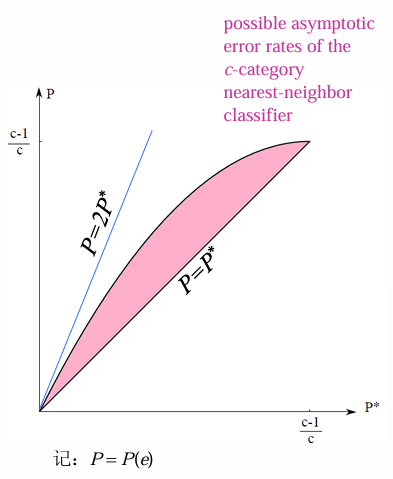
这个结论告诉我们：最近邻法的渐近错误率最坏不会超过两倍的贝叶斯错误率，而最好则有可能接近或达到贝叶斯错误率。

推导过程

• 最近邻规则的错误率：

$$P(e)=\int P(e|x)p(x)dx\\ P(e|x)=\int P(e|x,x')p(x'|x)dx',\quad （x'：x的最近邻）$$

当，（为的最近邻的概率）趋近以为中心的delta函数。对，假设和（最近训练样本，与独立）的类别标号分别为和，

$$P(\theta,\theta_n'|x,x_n')=P(\theta|x)P(\theta_n'|x_n')\\ P_n(e|x,x_n')=1 - \sum_{i = 1}^{c}P(\theta=\omega_i,\theta_n'=\omega_{i}'|x,x_n')=1 - \sum_{i = 1}^{c}P(\omega_i|x)P(\omega_i|x_n')\\ \lim_{n\rightarrow\infty}P_n(e|x)=\int\left[1 - \sum_{i = 1}^{c}P(\omega_i|x)P(\omega_i|x_n')\right]\delta(x_n' - x)dx_n'=1 - \sum_{i = 1}^{c}P^2(\omega_i|x)$$

• 渐近错误率

  $$P=\lim_{n\rightarrow\infty}P_n(e)=\lim_{n\rightarrow\infty}\int P_n(e|x)p(x)dx=\int\left[1 - \sum_{i = 1}^{c}P^2(\omega_i|x)\right]p(x)dx$$

• 1 - NN规则的错误界

  $$\sum_{i = 1}^{c}P^2(\omega_i|x)=P^2(\omega_m|x)+\sum_{i\neq m}P^2(\omega_i|x) （当P_i(i\neq m)相等时最小化）\\ P^*(e|x)=1 - P(\omega_m|x)（贝叶斯错误）\\ P(\omega_i|x)=\begin{cases}\frac{ P^*(e|x)}{c-1},&i\neq m\\1- P^*(e|x),&i=m\end{cases}\\ \sum_{i = 1}^{c}P^2(\omega_i|x)\geq(1 - P^*(e|x))^2+\frac{P^{*2}(e|x)}{c - 1}\\ 1 - \sum_{i = 1}^{c}P^2(\omega_i|x)\leq2P^*(e|x)-\frac{c}{c - 1}P^{*2}(e|x)$$

• 错误率

  $$P=\int\left[1 - \sum_{i = 1}^{c}P^2(\omega_i|x)\right]p(x)dx\Rightarrow P\leq2P^*\\ \text{Var}[P^*(e|x)]=\int\left[P^*(e|x)-P^*\right]^2p(x)dx\\=\int P^{*2}(e|x)p(x)dx - P^{*2}\geq0\Rightarrow\int P^{*2}(e|x)p(x)dx\geq P^{*2}$$

• 错误界

  $$P^*\leq P\leq P^*\left(2 - \frac{c}{c - 1}P^*\right)$$

K近邻分类器

在很多情况下，将决策建立在最近邻样本上有一定的风险。（数据分布复杂，存在噪声）

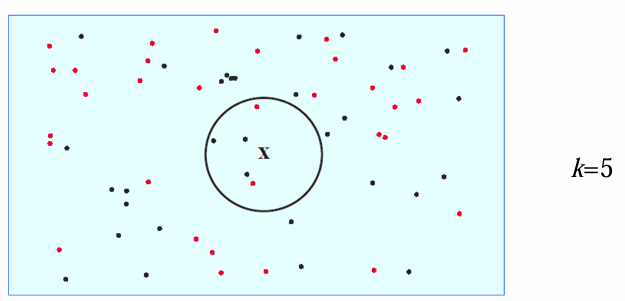
• 一种自然的改进就是引入投票机制：选择前个距离测试样本最近的训练样本，用它们的类别投票来决定新样本的类别。
• 给定训练集，对测试样本，设是在中的个最近邻样本。设类的判别函数，是中类样本的个数。
• 决策规则：

K近邻分类器与K近邻估计的关系

假设训练集包含个样本，其中类样本个，。

测试样本处，包含个最近邻样本的区域体积为，其中类样本个，。

则类条件概率密度和类先验概率的估计为：

$$p_n(x|\omega_i)=\frac{k_i}{nV},\quad p(\omega_i)=\frac{n_i}{n}$$

样本的类后验概率为：

$$p_n(\omega_i|x)=\frac{p_n(x|\omega_i)p(\omega_i)}{\sum_{j = 1}^{c} p_n(x|\omega_j)p(\omega_j)}=\frac{k_i}{k}\\ \omega_m = \text{arg max}_i \{p_n(\omega_i|x)\}$$

这就是近邻分类器.

K近邻的快速计算

• 搜索近邻的计算复杂度：—d:样本dim, n:训练样本数, K:测试样本数量
• 快速搜索策略：
  • 部分距离(partial distance)
  • 搜索树
  • 剪辑/压缩算法(pruning, condensing)

部分距离

$$\text{部分维度 }(r < d):\quad D_r^2(a,b)=\sum_{i = 1}^{r}(a_i - b_i)^2$$

如果部分平方距离已经超过当前最近邻的全局最小距离，可以提前停止后续维度的计算，从而节省计算时间。如果部分平方距离大于就终止计算。

搜索树

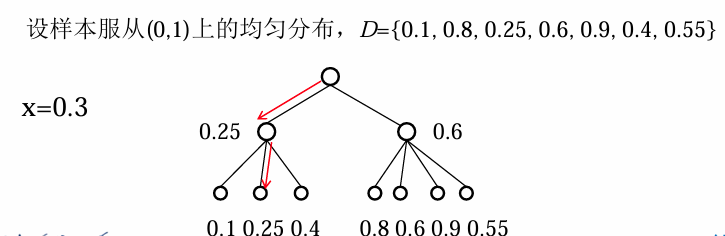
使用搜索树（例如 kd-tree）对训练样本进行组织，可以高效查找最近邻。基本思想是：

• 将样本按照特定规则划分成树状结构。
• 测试样本从根节点开始递归搜索，只访问相关子树，从而快速找到最近邻。

在实际应用中，kd-tree 是常用的搜索树结构，尤其适用于低维空间。

压缩近邻法

考虑近邻法的分类原理，远离分类边界的样本对于分类决策没有贡献。只要能够找出各类样本中最有利于与其它类相互区分的代表性样本，则可将很多训练样本去掉，简化决策过程中的计算。

压缩近邻法通过减少训练样本的数量来加速分类：

1. 删除冗余样本：对于类别边界之外的样本（远离决策边界的样本），它们对分类结果的贡献很小，可以删除。

2. 保留代表样本：通过算法挑选最能区分不同类别的样本点，形成代表性集合 。

3. 算法过程：

   • 将样本集分为两个活动的子集：和，前者称为储存集（Storage），后者称为备选集（GrabBag）。首先，在算法开始时，中只有一个样本，其余样本均在中。

   • 遍历中的每一个样本，如果采用中的样本能够对其正确分类，则该样本仍然保留在中，否则移动到中，从而扩大代表集合。依次重复进行上述操作，直到没有样本需要搬移为止。

   • 最后，用中的样本作为代表样本，对新来的样本进行分类。

距离度量

距离度量是模式分类的基础： 设有维空间的三个样本、和，记为一个的映射，如满足如下几个条件则为一个距离：

性质	对应公式
非负性
自相似性
对称性
三角不等式

距离可以描述点对间的相异程度，距离越大，两个点越不相似；距离越小，两个点越相似。

设，Minkowski距离度量定义如下：

$$d(x,y)=\left(\sum_{i = 1}^{d}|x_i - y_i|^q\right)^{\frac{1}{q}}$$

• 时，（城区距离/曼哈顿距离）
• 时，（欧氏距离）
• 时，（切比雪夫距离）

欧氏距离

$$x = \left[\begin{matrix}x_1\\x_2\\\vdots\\x_d\end{matrix}\right]\in R^d,\quad y = \left[\begin{matrix}y_1\\y_2\\\vdots\\y_d\end{matrix}\right]\in R^d\\ d(x,y)=\sqrt{\sum_{i = 1}^{d}(x_i - y_i)^2}=\left((x - y)^T(x - y)\right)^{\frac{1}{2}}$$

Mahalanobis（马氏）距离

设，定义如下：

$$d(x,y)=\sqrt{(x - y)^T M(x - y)}$$

（其中，是半正定矩阵）

• 为单位矩阵时，退化为欧氏距离。
• 为对角矩阵时，退化为特征加权欧氏距离。
• 由，，可看作是在新特征空间中的欧氏距离。

性质

距离对坐标变换敏感：

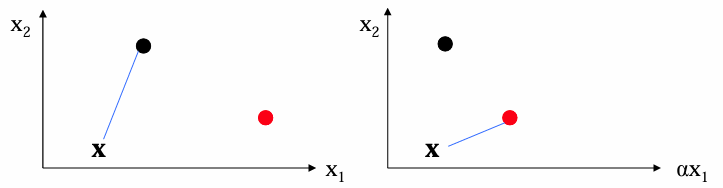
向量间距离的扩展：

• 分布间距离：KL散度、交叉熵
• 集合间距离：见chapter 9（聚类）

距离通常是无监督概念

• 如何利用先验知识、监督信息？

Tangent Distance（切向距离）

切向距离用于处理因 变换（如平移、旋转、缩放等）导致的样本相似性问题。

Q: 变换对距离的影响?

A: 例如：

• 图像的平移、旋转或缩放可能导致类内距离（同一类别样本的距离）变大，而超过类间距离（不同类别样本的距离）。
• 直接使用欧氏距离可能会导致错误分类。

定义

定义	说明
变换的参数化表示	给定一个样本,通过变换函数生成变换后的样本。:变换函数，:变换的参数(例如平移距离、旋转角度)
变换下的样本空间	样本 在变换 下生成的所有可能样本组成一个流形：
样本到的切向距离	定义到流形的最小距离是：（该距离对变换具有不变性）

线性近似流形

Q: 流形？

A: 流形（Manifold） 是数学中用来描述复杂形状的一种概念，可以看作是局部上类似于欧几里得空间的几何对象。它广泛应用于几何、物理学和机器学习中，尤其是在高维空间中建模复杂数据分布。

简单来说：局部像平坦的欧几里得空间，但全局可能是弯曲的。

例子：地球=二维流形，局部是二维平面、全局是球体。

由于流形 的结构可能复杂，我们可以用一个线性子空间近似它。

• 对变换的线性近似: 在点的泰勒展开，其中称为切向量（tangent vector）

  $$s(x,\alpha)=s(x,0)+\frac{\partial s(x,0)}{\partial\alpha}\alpha + O(\alpha^2)\approx x+\alpha T$$

• 用线性子空间近似:

• 样本到的切向距离：（到子空间的最小距离）

  $$\min_{\alpha}\vert \vert y-(x+\alpha T)\vert \vert$$

多参数变换

假设变换包含个变换参数：，例如：

分别表示旋转角度、水平位移、垂直位移

此时，变换下样本的表示:（样本空间中的维流形）

$$S_x=\{x'\vert \exists\alpha\in R^m \text{ for which } x' = s(x,\alpha)\}$$

对应的线性近似为：

$$\{x'\vert \exists\alpha\in R^m \text{ for which } x' = x+\sum_{i = 1}^{m}\alpha_i T_i\}$$

其中是第i个变换参数的切向量。

样本到的切向距离定义为：

$$\min_{\alpha\in R^m}\vert \vert y-(x+\sum_{i = 1}^{m}\alpha_i T_i)\vert \vert$$

距离度量学习

使用不同的距离度量，会得到不同的分类结果。

• 为了反映特征之间的关联关系
• 为了充分利用先验知识
• 反映特定问题的特定需求

在某些机器学习任务中（如聚类、分类等），我们需要定义一个适当的距离度量，用于衡量数据点之间的相似性或不相似性。

然而，标准的欧氏距离可能不足以捕捉数据的复杂关系，尤其是当有侧信息 (side information) 时，这些侧信息可以指导距离度量的优化。

假设我们有一组数据点 （位于 空间），并且有以下侧信息：

• Must-link 集合 S： 表示 和 应该是相似的（即，它们应该在同一类中）。
• Cannot-link 集合 D： 表示 和 应该是不相似的（即，它们应该属于不同的类）。

这些信息告诉我们哪些点需要在距离上更靠近，哪些点需要更远。

我们希望学习一个距离度量，使得：

• 对于 Must-link 对，点之间的距离尽可能小。
• 对于 Cannot-link 对，点之间的距离尽可能大。

为了实现这一目标，可以使用一个参数化的马氏距离 (Mahalanobis Distance)：

$$d_A(x, y) = \sqrt{(x - y)^T A (x - y)}$$

其中 是一个半正定矩阵（），用来学习距离度量。

优化目标：

$$\max_A \sum_{(x_i, x_j) \in D} d_A(x_i, x_j)\\ s.t.\sum_{(x_i, x_j) \in S} [d_A(x_i, x_j)]^2 \leq 1$$

• 希望 Cannot-link 集合中的点的距离尽可能大。

• 确保 Must-link 集合中的点的距离尽可能小。

• 保证 是一个半正定矩阵，使得距离 是有效的。