模式识别-Ch11-决策树

Ch11 决策树

[TOC]

决策树的基本概念

基本技术路线:属性选择、树构建、剪枝

1. 什么样的属性是好的？
2. 怎么建立这棵树？
3. 怎么剪枝？

决策树 非线性

定义：分类决策树是一种描述对样本进行分类的树形结构。决策树由节点和有向边组成。

• 内部结点：对于数据的一个特征/属性。
• 叶子结点：对应数据的一个类别。

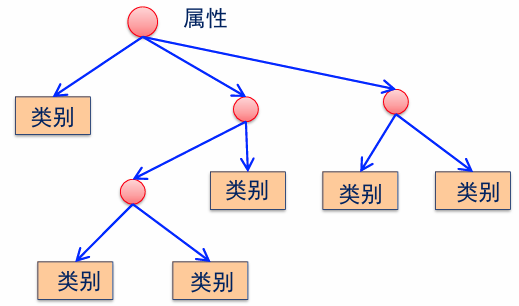
此时有很多的规则能够决定二分类、就不再是线性的分类器。

决策树规则代表实例属性值约束的合取（交集）的析取（并集）式。

Q: 属性是连续的怎么办？将连续转化为离散的。

假如是二叉树，就要把属性分成两个子集，并起来=全集。

所以连续属性：(1)子集=区间。(2)按分布分配区间

例：连续属性

决策树将特征空间划分为 轴平行的（hyper-）矩形 区域（如图中的绿色边界）。每个矩形区域（或超立方体）对应于一个类别标签（例如，0 或 1），或者是概率分布。

决策树的每一条 从根到叶的路径 对应于特征空间中的一个区域 R。

• 这些区域由条件划分（如 、）定义。
• 树的叶子节点定义了最终的分类结果。

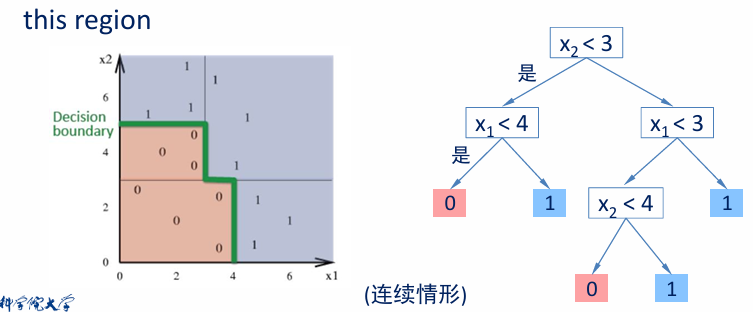
图中：

• 左侧是二维特征空间的划分，绿色边界将数据划分为不同区域。
• 右侧是对应的决策树，展示了如何通过属性测试（如）逐步划分空间。

决策树的复杂性与数据几何的关系：

决策树的复杂性与数据在特征空间中的分布密切相关：

1. 数据越复杂（例如分布具有很多不规则边界），树的复杂性越高。
2. 简单的数据分布（例如，线性分布）会导致简单的决策树。

构建决策树

一般技术路线：

1. 决策树生成：遍历所有可能的特征属性、对树进行分支。
2. 决策树剪枝：适当剪除一些不必要的分支，减少过拟合，获得更好的推广能力。

决策树学习

ID3、C4.5、CART区分点、优缺点

这三种算法构建树、剪枝的过程一样；只是选择属性的规则不同。

决策树构建的技术路线

1. 构建根结点，将所有训练数据都放在根结点。
2. 选择一个“最优”特征，按照它的离散取值，将上一个节点中数据分割成不同子集。
3. 对于分割的子集，如果能够基本正确分类（即：子集中大部分数据都属于同一类），那么构建叶结点。
4. 对于不能构建叶结点的子集，继续2 - 3步，直到所有子集都能构建叶结点。

核心任务：如何选择“最优”特征，对数据集进行划分？

信息论相关基础—选择属性的依据

熵(Entropy): 表示随机变量不确定性的度量。

设是一个取有限个值的离散随机变量，其概率分布和熵的定义为：

$$P(X=x_i)=p_i,\quad i=1,2,\dots,n\\ H(x)=\sum_{x\in X}p_i\log p_i$$

条件熵：设有随机变量，其联合概率分布为：

$$P(X=x_i,Y=y_j)=p_{ij},\quad i=1,2,\dots,n;\ j=1,2,\dots,m$$

条件熵表示在已知随机变量的条件下随机变量的不确定性。

$$Ent(D)=H(Y|X)=\sum^n_{i=1}P(X=x_i)H(Y|X=x_i)=\sum^n_{i=1}p_iH(Y|X=x_i)$$

信息增益(互信息): 一个属性的不确定性。在某特征信息X已知的时候，是类Y信息的不确定性减少的程度。

$$Gain(D)=g(D,A)=H(D)-H(D|A)$$

决策树学习中：信息增益=训练数据集中类与特征的互信息。

基于信息增益的特征选择：对训练数据集(或子集)，计算其每个特征的信息增益、选择信息增益最大的特征。

信息增益率/增益比

$$\text{Gain\_ratio}(D,a)=\frac{Gain(D,a)}{Ent(D|a)}\\ Ent(D|a)=\sum^V_{j=1}\frac{|D^i|}{|D|}Ent(D^i)$$

基尼值/基尼指数CART

1. 基尼值（Gini）

   • 假定样本集合中第类样本所占比例为，，则样本集合的基尼值定义为： $$Gini(D)=\sum_{i = 1}^{C}\sum_{j\neq i}p_ip_j = 1-\sum_{i = 1}^{C}p_i^2$$ 基尼值越小，纯度越高。

2. 基尼指数（Gini Index）

   • 属性的基尼指数：利用属性对样本集合划分后的加权基尼值之和。 $$Gini\_index(D,a)=\sum_{i = 1}^{v}\frac{\vert D^i\vert}{\vert D\vert}Gini(D^i)$$

决策树生成

决策树划分的目的：每一个分支结点包含的样本尽可能属于同一类别，即分支结点的“纯度”尽可能高。

评价子集“纯度”的方法：给定一个特征对数据集合进行划分，如何评价划分后子集的“纯度”？

评价方法	对应的算法
信息熵	ID3
增益率	C4.5
基尼指数	CART分类
平方误差最小(MSE)	CART回归

决策树生成算法

ID3

利用分割前后的熵来计算信息增益，作为判别能力的度量。

类似于极大似然法进行概率模型的选择。

偏好选择取值数量最多的属性。

核心：在决策树的各个结点上应用信息增益准则来选择特征，递归地构建决策树。

简述方法：从根结点开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。

C4.5

来自于ID3，稍微改进。

• 选择增益率 而不是 信息增益
• 可以在树构造的过程剪枝
• 能够对连续属性的离散化处理
• 能够对不完整数据进行处理

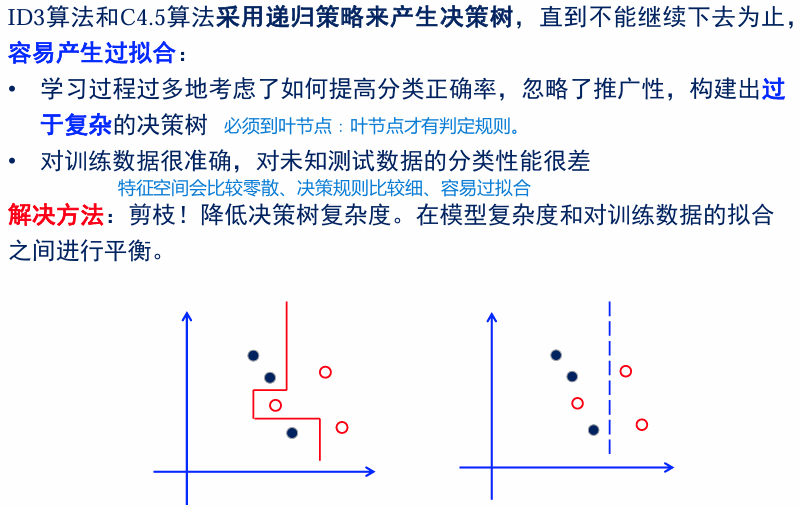
决策树剪枝的基本原则

如何避免overfitting?

• 去除不相关的特征：对分类没有帮助
• 增加训练样本

预剪枝

例：预剪枝

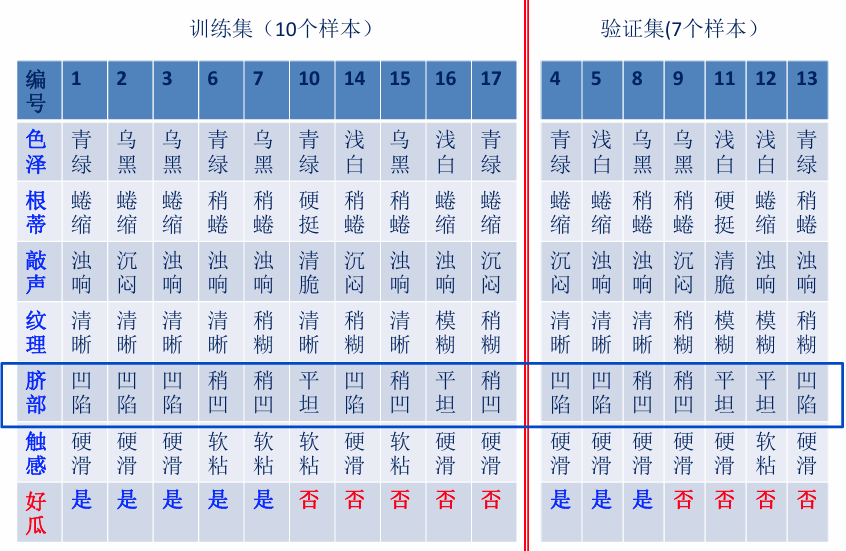
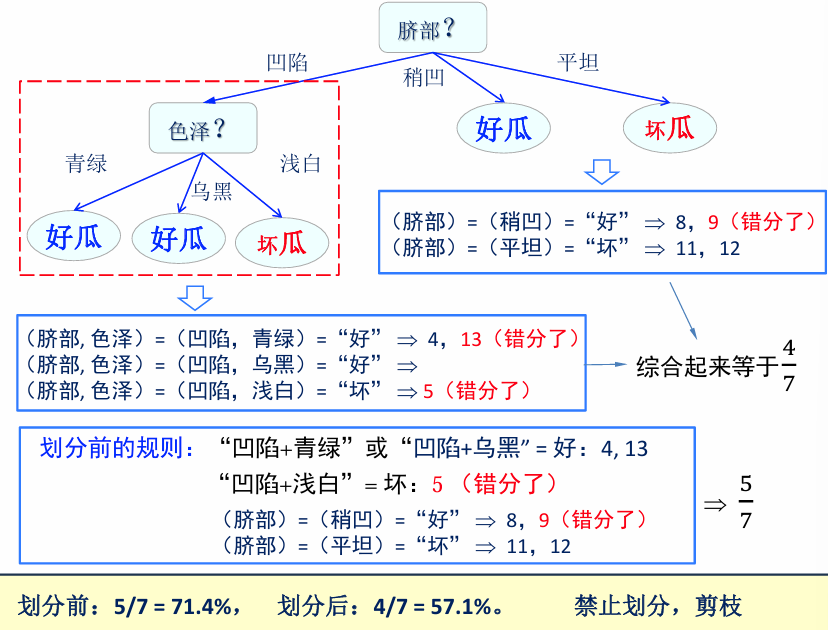
最终的结果是：

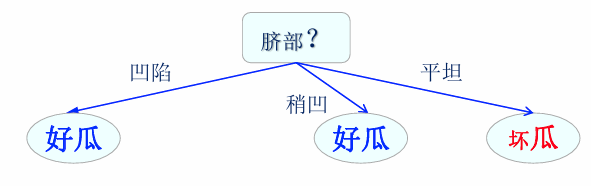
后剪枝

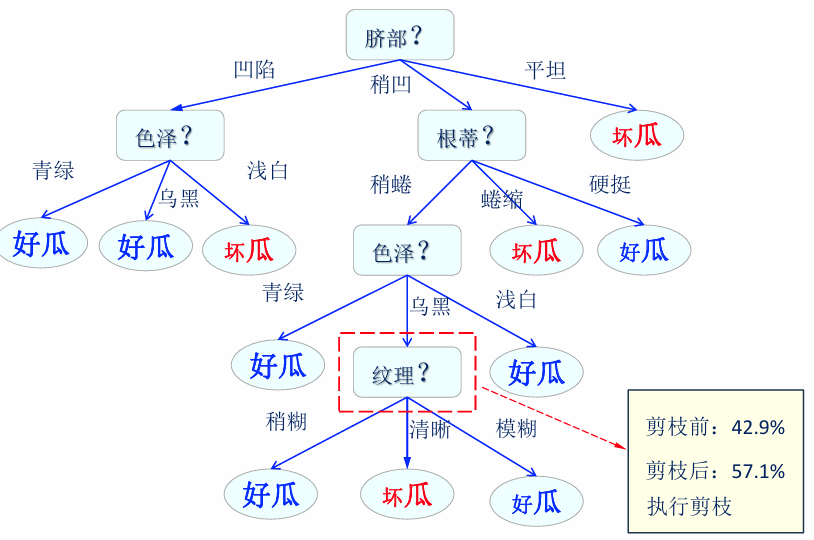
最终剪枝结果：

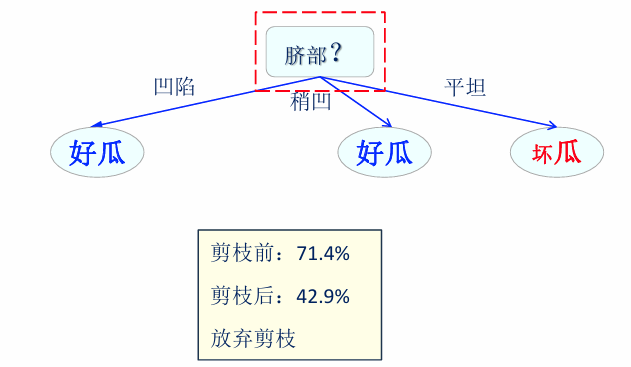
缺失值处理

对于不完整样本（某些属性值缺失的样本），存在以下两个问题：

1. 属性值缺失的情况下，如何进行划分属性选择？
2. 给定划分属性，若样本在该属性上的值缺失，如何对样本进行划分？

处理方法

为每个样本分配一个权重（通常考虑样本具有相同的权重）。

• A1：使用所有包含给定属性值的样本集合计算属性的信息增益/增益率/基尼指数。
• A2：划分至该属性的所有子结点，并根据子结点所占父结点比例调整权值。

相关公式

记为样本集合中属性上没有缺失值的样本子集；表示在属性上取值为的样本子集。

$$Gain(D,a)=\rho\times Gain(\widetilde{D},a)\\ \rho=\frac{\sum_{x_{i}\in\widetilde{D}}w_{i}}{\sum_{x_{i}\in D}w_{i}}$$

表示无缺失值样本所占的比例；这里表示样本的权重。

连续值处理

离散特征：只能取固定个数的值，可依具体取值进行结点划分。

连续特征：无限取值，不能根据具体特征取值对结点进行划分。

连续特征离散化：通过设置一定的取值区间，将连续取值转化成离散的区间取值。常用的离散策略是二划分。对于连续特征，其离散函数可表示为：

$$f(x)=\begin{cases}0, & x > t\\1, & x\leq t\end{cases}$$

给定样本集和连续属性，假定在上出现了个不同的取值，将这些值从小到大进行排序，记为。

基于划分点，可将分为和两个子集，其中包含那些在属性上取值大于的样本，而包含那些在属性上取值不大于的样本。

划分点的计算公式为：

$$T_{i}=\frac{a^{i}+a^{i + 1}}{2},\quad1\leq i\leq n - 1$$

信息熵与信息增益的计算

• 根据连续属性和阈值，对进行划分，整个集合的信息熵变为：

  $$Ent(D|a,t)=\frac{\vert D_{t}^{+}\vert}{\vert D\vert}Ent(D_{t}^{+})+\frac{\vert D_{t}^{-}\vert}{\vert D\vert}Ent(D_{t}^{-})$$

• 根据连续属性和阈值，对进行划分所获得的信息增益：

  $$Gain(D,a,t)=Ent(D)-Ent(D|a,t)$$

• 在特征选择的同时，确定合适的阈值（使得信息增益最大）：

  $$\max_{t\in\{T_{1},T_{2},\cdots,T_{n - 1}\}}Gain(D,a,t)$$

CART决策树

有监督学习、基尼系数、回归问题

• CART同样由特征选择、树的生成及剪枝组成，既可以用于分类也可以用于回归，以下将用于分类与回归的树统称为决策树 。
• CART是二叉树，内部结点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支 。
• 该决策树等价于递归地二分每个特征，将输入空间（即特征空间）划分为有限个单元，并在这些单元上确定预测的概率分布，即在输入给定的条件下输出的条件概率分布。

算法实现

分类树

回归树

构建回归树：递归地选择最优的特征属性和其划分值，将当前数据空间划分为两部分，直到满足停止条件。

• 离散特征：划分属性0/1(是/不是)—西瓜色泽青绿=0/1

• 连续特征：与划分值s的大小关系

  $$D^-(j,s)=\{x|x^j\le s\},D^+(j,s)=\{x|x^j> s\}$$

• 停止条件：

  1. 结点中样本个数小于预定阈值
  2. 没有可用特征
  3. 决策误差小于预定阈值

特征选择：使用平方误差最小(MSE)准则，遍历所有特征j和可能的划分值s，选择是的预测平方误差最小的组合，同时记录对应的均值，作为决策函数相应区域的取值。

$$\arg\min_{j,s}\left[\sum_{x_i\in D^+(j,s)}(y_i-m^+)^2+\sum_{x_i\in D^-(j,s)}(y_i-m^-)^2\right]$$

CART 剪枝

1. 决策树生成

   • 基于训练数据集生成决策树，生成的决策树要尽量大。

2. 决策树剪枝

   • 用验证数据集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。
   • 决策树的生成就是递归地构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数(Gini index)最小化准则，进行特征选择，生成二叉树。

3. 剪枝的进一步解释

   • 在终止条件被满足，划分停止之后，下一步是剪枝。
   • 给树剪枝就是剪掉“弱枝”，弱枝指的是在验证数据上误分类率高的树枝。
   • 对树剪枝会增加训练数据上的错误分类率，但精简的树会提高新记录上的预测能力。
   • 剪掉的是最没有预测能力的枝。

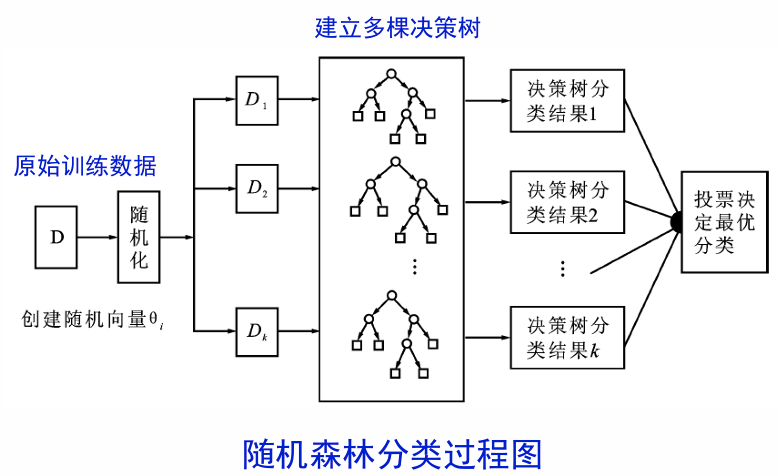
决策树推广-随机森林

随机森林：通过随机方法构建多个决策树，利用决策树分类结果进行投票，得到随机森林的分类结果。随机森林泛化能力更强。

两个随机：在生成决策树之前，先采用两个随机方法确定可用的训练数据和特征属性。

• 训练数据随机：随机采样一部分训练数据。
• 使用特征随机：随机选择一部分特征属性。

算法实现

该算法用随机的方式建立起多棵决策树，然后由这些决策树组成一个森林，其中每棵决策树之间没有关联，当有一个新的样本输入时，就让每棵树独立的做出判断，按照多数原则决定该样本的分类结果。

基本任务：

1. 构建随机森林
2. 使用随机森林预测

在建立好了随机森林之后，我们对于来的新的样本要进行预测。

基本步骤(分类)：

1. 向建立好的随机森林中输入一个新样本
2. 随机森林中的每棵树都能够独立地做出判断
3. 投票，将得到票数最多地分类结果作为该样本地最终类别

分类：投票取票数最多；回归：取均值。

总结

• 决策树的构建是一种递归过程。
• 每次选择的属性需要满足某种优化准则（例如最大化信息增益，最小化基尼指数等）。
• 决策树的结果是一个树状结构，其中每个内部节点是一个测试条件，每个叶子节点是一个类别标签。

决策树优缺点

离散数据的情况下适合使用决策树。

ID3 vs C4.5

随机森林的影响因素和优点

影响因素：

1. 森林中单颗树的分类强度：分类强度↑，分类性能↑
2. 森林中树之间的相关度：相关度↑，分类性能↓

优点：

决策树原理、规则、优缺点、哪个指标对应哪个算法

RF的基本技术路线、

C4.5的构建过程：离散/连续、剪枝原则