模式识别-Ch10-SVM

Ch10 SVM

[TOC]

1-nn vc 维：

vc维是理论的，实际上难以计算。

Hard-Margin SVM

间隔(Margin)：分类超平面到最近支持向量之间的距离。

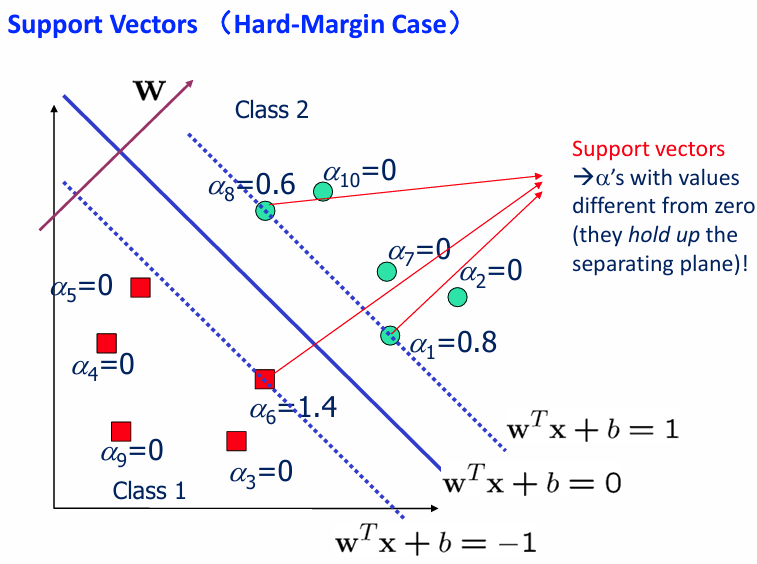
支持向量(Support Vec)：那些对分类边界的 位置 和 形状 起到关键作用的样本点。支持向量是离分类超平面最近的点。边界完全由支持向量决定。

估计Margin

两类情形的决策面方程：

对于任意样本，将其向决策面投影：,w是法向量。

代入决策函数：

$$\begin{align} g(x)&=w^T\left(x_p+r\frac{w}{\|w\|}\right)+b\\ &=r\|w\|\\ r&=\frac{g(x)}{\|w\|} \end{align}$$

法向量和决策面上向量做内积=0；且w是单位法向量，后一项二者平行。

决策面到原点的距离：(b也与法向量平行)

计算点x到决策面的距离, margin距离决策面的距离是最近的(min):

$$d(x)=\frac{|w^Tx+b|}{\sqrt{\|w\|^2_2}}=\frac{|w^Tx+b|}{\sqrt{\sum^d_{i=1}w_i^2}}\\ margin=\arg\min_{x\in D}\{d(x)\}=\arg\min_{x\in D}\frac{|w^Tx+b|}{\sqrt{\sum^d_{i=1}w_i^2}}$$

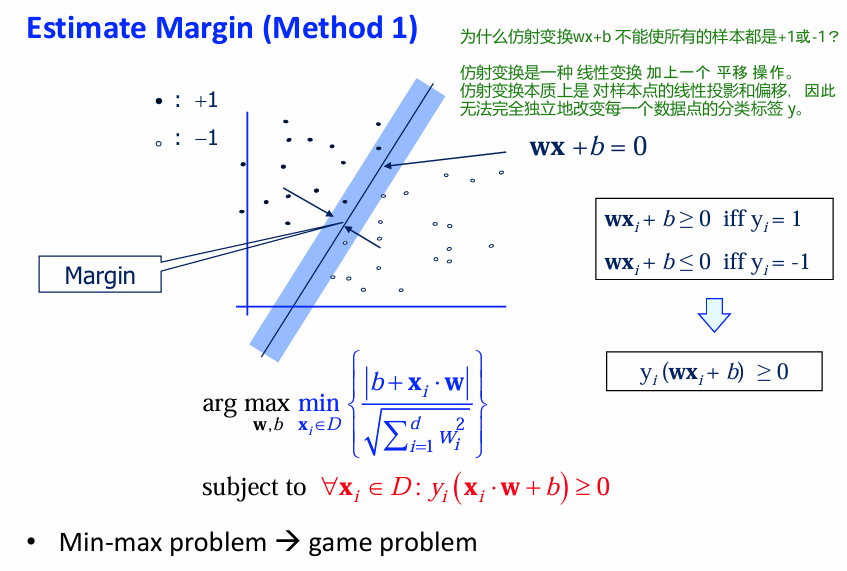
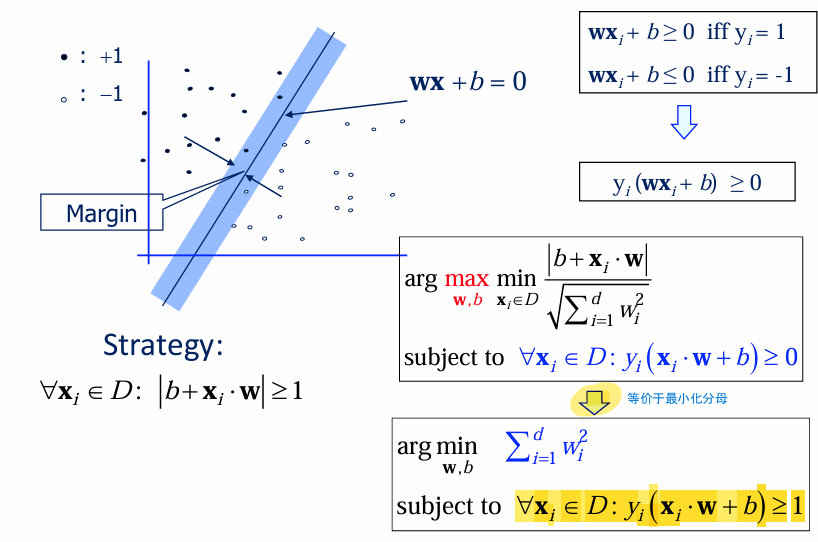
原来的形式是：

$$\arg \max_{w,b} \min_{x_i \in D} \frac{|b + x_i \cdot w|}{\|w\|}$$

这表示在所有可能的超平面参数 中，我们希望最大化支持向量距离超平面的最小间隔。但我们现在规定最小间隔=1，这消除了“min”的计算。优化目标从“最大化间隔”变为“最小化” w 的长度（即 ）：

该形式可以转化成:

$$\arg \min_{w,b} \frac{1}{2} \|w\|^2 \\ \text{s.t. } y_i (w \cdot x_i + b) \geq 1, \forall x_i \in D\\$$

Margin与超平面的关系

Margin: 两类数据之间的决策边界的宽度（即支持向量与超平面之间的距离的两倍）。

SVM目标: 找到使 Margin 最大的超平面（即“最大间隔分类器”）。

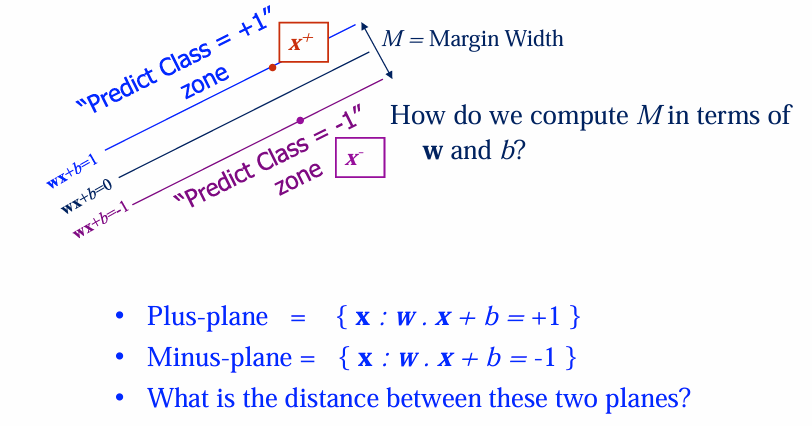
• 是分类决策边界。
• 和是两条平行于决策边界的支持向量平面。
• 决策边界是中间线，支持向量位于两个平行平面上。

Q：图中提出了问题“如何用 w和b来计算 Margin 宽度 M？。

A: 给定两个平行超平面（公式如 ` 和 ），两平面之间的距离计算公式是：

类比到支持向量机中：

• 对应的 是超平面法向量 。
• 两平面和的距离：

线性可分支持向量机求解

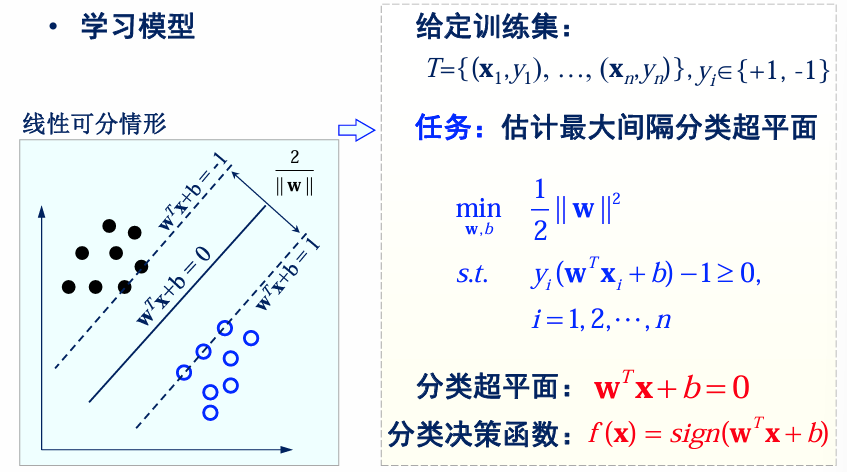
通过二次规划求解

求解线性可分支持向量机 (SVM) 的最优解通常可以通过 二次规划（Quadratic Programming） 方法完成，而这可以用 拉格朗日乘子法 实现。

线性可分SVM的目标函数是二次凸函数、约束条件是线性的，因此可以使用二次规划求解SVM。

拉格朗日乘子法求解—不记

写上来只是为了逻辑的连贯性。

对于问题：

$$\arg \min_{w,b} \frac{1}{2} \|w\|^2 \\ \text{s.t. } y_i (w \cdot x_i + b) \geq 1, \forall x_i \in D\\$$

该形式符合凸优化理论，可以使用拉格朗日乘子法解决问题（Lagrangian Dual Problem）

$$\mathcal{L}=\frac 1 2||w||^2-\sum\alpha_i[y_i*(w\cdot x_i+b)-1]$$

: Lagrange Multiplier

对求解偏导：

$$\frac{\partial \mathcal{L}}{\partial w}=w-\sum\alpha_iy_ix_i=0\\ w=\sum\alpha_iy_ix_i\\\\ \frac{\partial \mathcal{L}}{\partial b}=\sum\alpha_iy_i=0$$

• : is a weighted sum of the input vectors ( )
• 很多情况下: because this point doesn’t contribute to the margin

再把代进中，使得中没有，只有一个参数。

$$\begin{align} \mathcal{L}=&\frac 1 2w^Tw-\sum\alpha_i[y_i*(w\cdot x_i+b)-1]\\ =&\frac 1 2 (\sum\alpha_iy_ix_i)(\sum\alpha_jy_jx_j)-\sum\alpha_i[y_i\sum\alpha_jy_jx_j\cdot x_i]+b\sum\alpha_iy_i+\sum\alpha_i\end{align}$$

因为：

$$\begin{align} \mathcal{L}=&\frac 1 2 (\sum\alpha_iy_ix_i)(\sum\alpha_jy_jx_j)-\sum\alpha_i[y_i\sum\alpha_jy_jx_j\cdot x_i]+\sum\alpha_i\\ =&\sum\alpha_i-\frac 1 2 (\sum\alpha_iy_ix_i)(\sum\alpha_jy_jx_j)\\ =&\sum\alpha_i-\frac 1 2 \sum_i\sum_j\alpha_i\alpha_jy_iy_jx_ix_j \end{align}$$

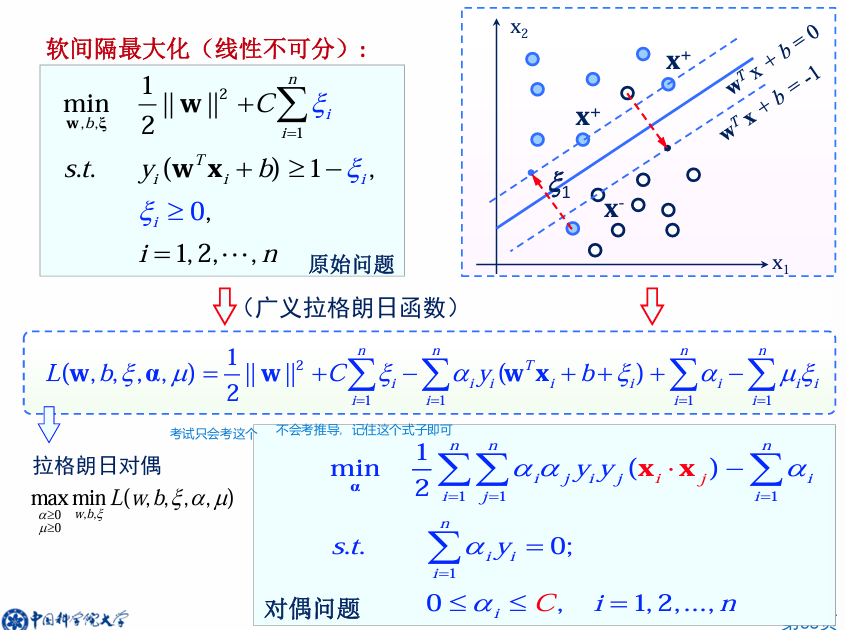
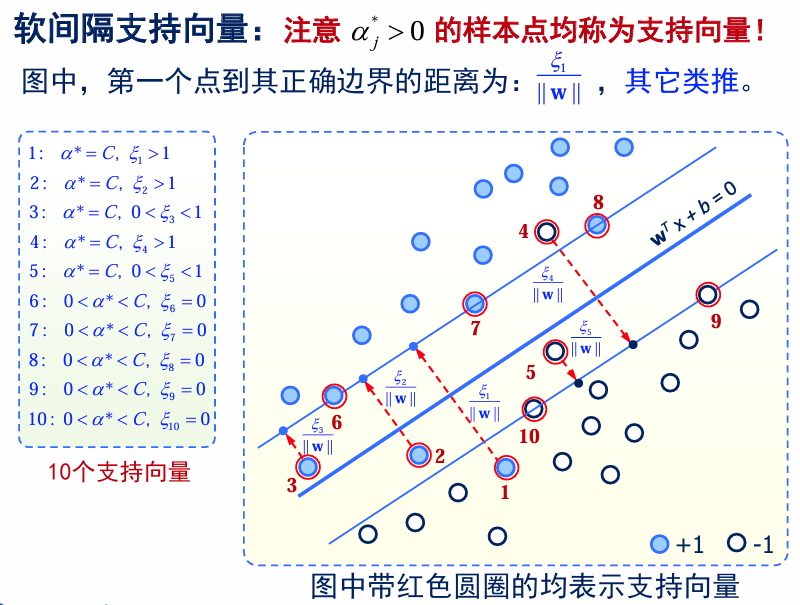
Soft-Margin SVM

不具有线性可分性的情况下：SVM 原始模型（线性可分 SVM）假设数据是完全线性可分的。但在实际数据中，通常会有一些噪声点（如图中的白点和黑点的异常位置），导致数据集不可线性完全分离。这就需要对原始目标函数进行修改，以适应有噪声的数据。

软间隔 SVM 的优化问题如下：第一项体现了模型的 表达能力（间隔最大化，偏向于低方差）；第二项体现了模型的 经验风险（分类错误惩罚，偏向于低偏差）。

$$\min \frac 1 2 ||w||^2+C\sum^m_i\xi_i\\ s.t.\ y_i*(w\cdot x+b)\ge 1-\xi_i\\ \xi_i\ge0\\ i=1,2,\dots,n$$

：表示第 个样本的松弛变量（slack variable），用于量化样本允许的分类错误或间隔违规程度。C：是一个权衡参数，用于平衡 间隔最大化 和 分类错误惩罚 之间的权重。对于参数:

• Low C: 对分类错误更宽松，更倾向于允许一些错误以换取更大的间隔。(欠拟合)
• High C: 更严格地惩罚分类错误，强制模型尽量避免分类错误，即 错误的代价很高。(易导致过拟合)

合页损失(Hinge Loss): 一种常用的损失函数。Hinge Loss用于衡量样本的分类错误和分类边界的间隔。其在soft-margin中的定义如下：

$$\min \frac 1 2||w||^2+C\sum^m_i\max(0,1-y_i*(w\cdot x+b))$$

: 表示样本的真实标签（通常为-1或1）

: 表示样本的预测分类（即决策函数输出的值）。

Hinge Loss的目标是使正确分类的样本的损失为0，并增大错误分类样本的损失。在软间隔分类中，Hinge Loss通常与正则化项结合使用，以平衡分类错误和模型复杂度。通过最小化Hinge Loss和正则化项，可以得到一个具有较小间隔违规和较小模型复杂度的分类模型，从而在训练集上和测试集上获得良好的性能。

对偶问题(Dual)

什么是对偶问题？ 在约束优化问题中，可以通过拉格朗日对偶性将原始问题（主问题）转换为对偶问题，目的是使问题的求解更简单或更高效。

为什么使用对偶问题？

• 对偶问题往往比原始问题更易求解，尤其是在 SVM 的情况下，使用对偶问题可以更自然地引入核函数，扩展到非线性分类问题。
• 对偶问题的解与原始问题的解是等价的（强对偶性），因此我们可以通过求解对偶问题间接得到原问题的解。

对偶问题求解

$$\nabla_w L(w,b,\alpha)=w-\sum^n_{i=1}\alpha_iy_ix_i=0\Rightarrow w=\sum^n_{i=1}\alpha_iy_ix_i=0\\ \nabla_b L(w,b,\alpha)=\sum^n_{i=1}\alpha_iy_i=0$$

将得到的偏导代入中：

$$\begin{align} \min_{w,b} L(w,b,\alpha)&=\frac 1 2(\sum^n_{i=1}\alpha_iy_ix_i)^T(\sum^n_{j=1}\alpha_jy_jx_j)-\sum^n_{i=1}\alpha_i y_i((\sum^n_{j=1}a_jy_jx_j)^Tx_i)+\sum^n_i\alpha_i\\ &=-\frac 1 2 \sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum^n_{i=1}\alpha_i \end{align}$$

求对的极大

$$\max_{\alpha} \min_{w,b} L(w,b,\alpha)=\max_{\alpha} -\frac 1 2 \sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum^n_{i=1}\alpha_i\\ \iff \min_{\alpha}\frac 1 2 \sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum^n_{i=1}\alpha_i\\ s.t. \sum^n_{i=1}\alpha_iy_i=0\\ a_i\ge 0,i=1,2,\dots,n$$

对偶问题本质上是一个 凸二次规划问题（convex quadratic programming, QP），其目标函数是凸的。在凸优化问题中，最大化凸函数等价于最小化其负值。

最终对偶问题被转化为一个标准的二次规划问题，既可以通过数学工具（如拉格朗日法）手动求解，也可以利用已有的优化算法（如SMO算法）求解。对于凸优化问题，全局最优解总是可以找到。

对偶问题的KKT条件

$$\begin{align} &\alpha_i^*\ge 0\\ &y_i(w^{*T}x_i+b^*)-1\ge 0 \\ &a_i^*(y_i(w^{*T}x_i+b^*)-1)=0 \end{align}$$

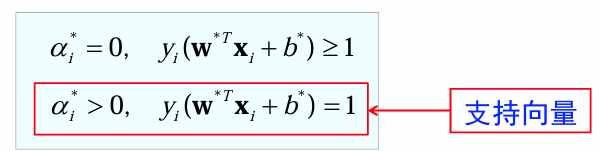
总结

• Margin 是指两类数据之间的决策边界的宽度（即支持向量与超平面之间的距离的两倍）。
• SVM 的目标是找到使 Margin 最大的超平面（即“最大间隔分类器”）。
• 支持向量是距离分类超平面最近的点，它们决定了 Margin 的大小。

SVM 的步骤

1. 准备数据矩阵：收集训练数据集 ，其中 是特征向量， 是对应的标签。
2. 选择核函数：核函数用于将低维数据映射到高维空间，例如线性核、高斯核等。
3. 选择误差参数 C：C 是一个超参数，用于控制分类的软边界（软间隔）的惩罚。
4. 训练系统：利用二次规划（QP）算法求解 和 。
5. 分类新数据：训练完成后，使用支持向量和对应的 值对新数据进行分类。

弱点

1. 训练（测试）速度慢：原因：需要解决约束的二次规划问题（QP），尤其在大数据集上计算复杂度较高。
2. 本质上是一个二分类器：默认情况下只能处理二分类问题，需要扩展才能解决多分类任务（如一对一、一对多策略）。
3. 对噪声非常敏感：数据集中少量的异常点（outliers）可能显著影响分类边界。
4. 核函数选择的困难：
   • 没有统一的理论指导如何选择最优核函数，这在实际应用中是一大挑战。
   • 一旦选择核函数后，超参数 C 是唯一的可调节参数。

优点

1. 训练相对容易：不需要像神经网络（NN）那样处理局部最小值问题，SVM 的解是全局唯一的。
2. 不受维度灾难的影响：通过核技巧，SVM 能够在高维空间中运行，但仍然只需要计算点积，从而避免了维度灾难问题。
3. 不易过拟合：最大间隔约束使得模型对数据的泛化能力较强。
4. 几何解释简单：通过构造最大间隔超平面，几何意义清晰直观，不需要复杂的网络结构。