模式识别-Ch3-参数估计
Ch3 参数估计-最大似然和贝叶斯参数估计
不考EM、HMM

基本概念
贝叶斯分类器: 已知类先验概率
但类先验概率和类条件概率密度在实际中往往是未知的。
因此,我们要换一种处理问题的方式:“从样本出发来设计分类器”。根据设计方法,可以将分类器分为两类:
- 估计类先验概率和类条件概率密度函数(产生式方法)
- 直接估计类后验概率或判别函数(判别式方法)
| 参数估计 | 非参数估计 |
|---|---|
| 样本所属的类条件概率密度函数的形式已知,而概率密度函数的参数是未知的。 | 样本所属的类条件概率密度函数的形式和参数都是未知的。 |
| 目标是由已知类别的样本集估计概率密度函数的参数。 | 目标是由已知类别的样本集估计类条件概率密度函数本身。 |
| 例如,知道样本所属总体为正态分布,而正态分布的参数未知 |
—- |
| 基本概念 | 说明 | 例子 |
|---|---|---|
| 统计量 | 样本中包含总体的信息,我们希望通过样本集将有关信息估计出来。根据不同要求构造出有关样本的某种函数,在统计学中称为统计量 |
|
| 参数空间 | 将未知待估计参数记为 |
—- |
| 点估计 | 点估计问题就是构造一个统计量 |
常用的均值估计: |
| 区间估计 | 与点估计不同,区间估计要求采用 |
—- |
最大似然估计
基本假设
- 独立同分布假设:每类样本均是从类条件概率密度
中独立抽取出来的。 具有确定的函数形式,只是其中的参数 未知: - 比如,当
服从一维正态分布 ,未知的参数为 ,为一个二维向量。
- 比如,当
- 各类样本只包含本类的分布信息:即不同类别的参数是独立的。可以分别处理
个独立问题。
基本原理
已知随机抽取的
直观想法:一个随机试验如有若干个可能的结果:A,B,C,…。若仅作一次试验,结果A出现,则认为试验条件(模型参数)对A出现有利,也即A出现的概率很大。
一般地,事件A发生的概率与参数
设样本集包含
方法描述
令
如果
为计算方便,通常采用对数似然函数:
问题求解
当
用梯度上升法求解
| 当 |
当 |
|---|---|
| 梯度等于0是最优解的充要条件 | 梯度等于0是最优解的必要条件 |
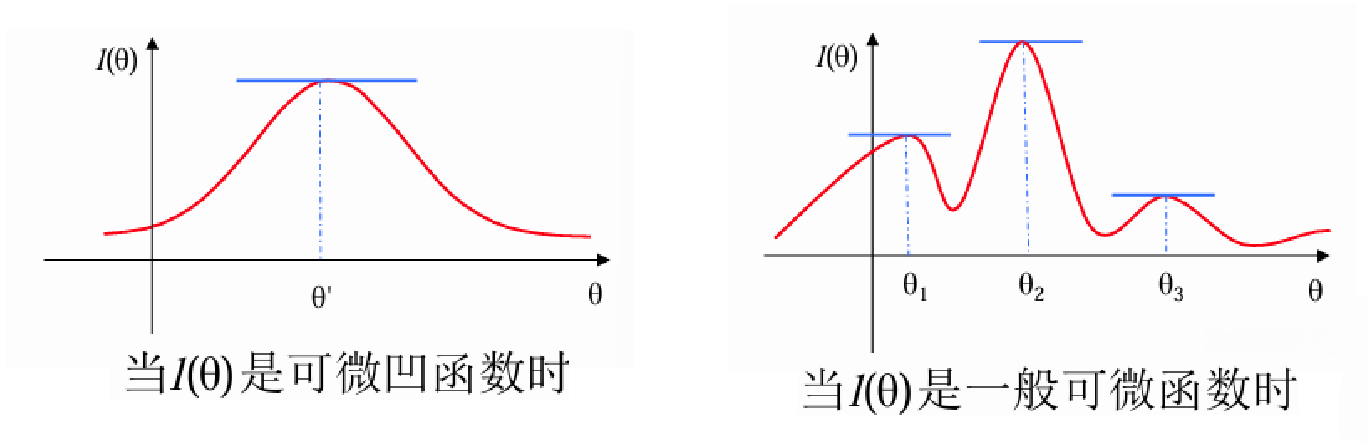
在高维空间中,寻找全局最优解是极困难的,通常满足于局部最优解。
例1:黑白球
一个袋子里装有白球与黑球,但是不知道它们之间的比例。现有放回地抽取10次,结果获得8次黑球2次白球,估计袋子中的黑球的比例。
最大似然估计法:设抽到黑球的概率为p,取到8次黑球2次白球的概率为:
例2:高斯分布下的最大似然估计
总的来说,这边就是一个很简单的多元正态分布求解MLE,非常简单。在多元统计分析里面也算过了。
预备公式:
已知
概率密度函数为:
对数似然函数为:
似然函数求导:
估计
估计
一维情况:
贝叶斯估计
贝叶斯估计是概率密度估计中另一类主要的参数估计方法。其结果在很多情况下与最大似然法十分相似,但是,两种方法对问题的处理视角是不一样的。
| 贝叶斯估计 | 最大似然估计 |
|---|---|
| 将待估计的参数视为一个随机变量,其中的一个核心任务是根据观测数据对参数的分布进行估计。 | 将待估计的参数当作未知但固定的变量,其任务是根据观测数据估计其在参数空间中的取值。 |
| $p(x\vert D)\sim N(\hat{\mu}_{n},\sigma^{2})\\hat{\mu}_{n}=\frac{1}{n}\sum_{i = 1}^{n}\mathbf{x}_{i}$ |
上面公式给出的是一维下估计。
基本方法
参数先验分布
给定样本集
利用贝叶斯公式计算参数的后验分布
对于一般情况,计算
可得贝叶斯参数估计中的后验概率密度函数:
Q: 如何使用
获得关于数据的分布? 得到
只是获得了关于参数 的后验分布,并没有像最大似然估计那样获得参数 的具体取值。
方法1 方法2 方法3 对 采样,计算平均值 最大后验估计(Maximum A Posteriori estimation, MAP) 后验数据分布(完整的贝叶斯方法) PR/ML方法中普遍使用的L2正则,等价于假设参数服从
后验数据分布
最终目的:根据
比如,假定观测样本服从正态分布
但现在获得了有关
考虑全概率公式和边际分布:
: 在给定参数 时,样本分布与训练集 无关 : 不同参数的密度函数的加权平均
积分通常很难计算,使用蒙特卡洛近似方法: 是
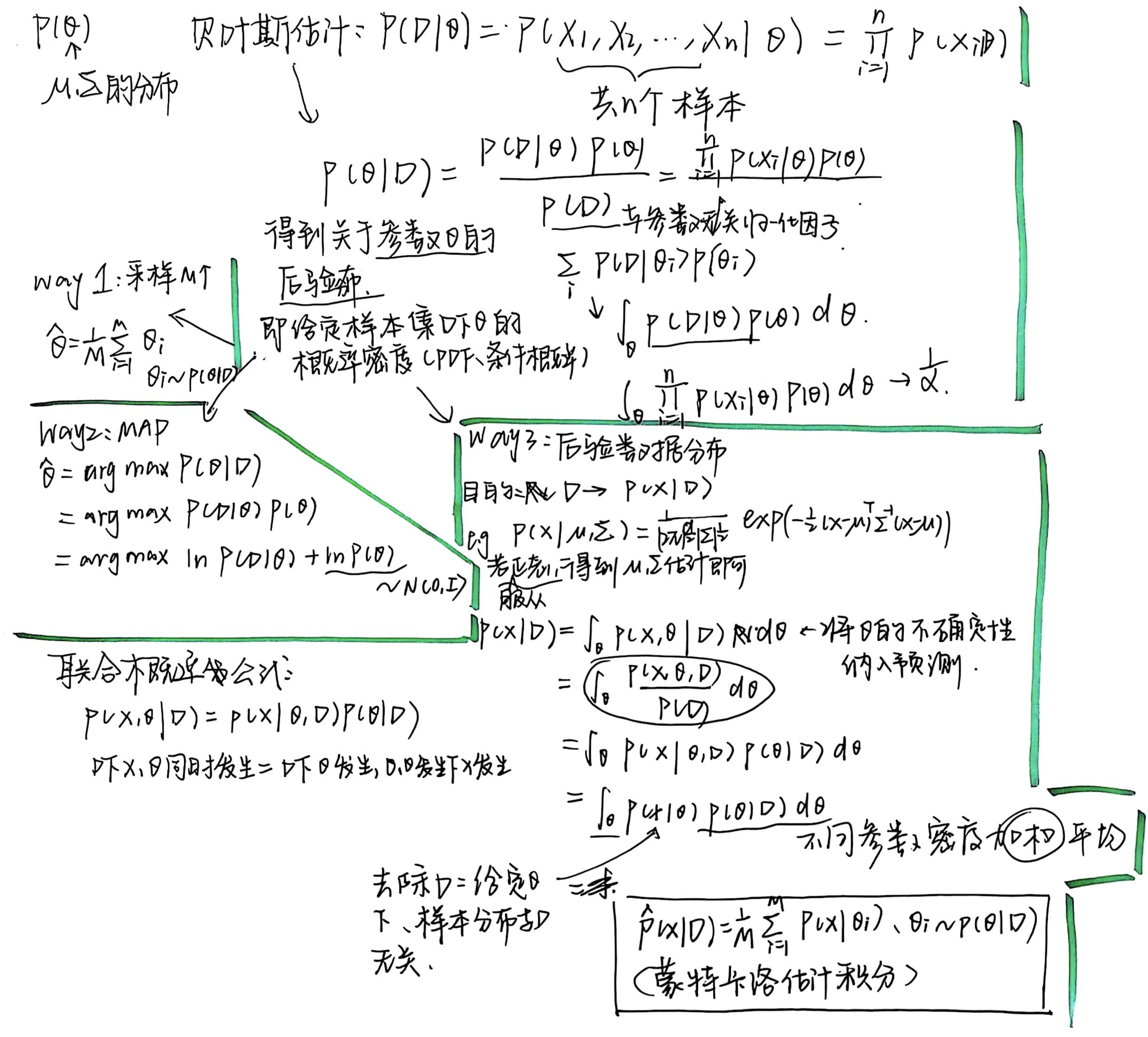
一维情形:假定
假定参数
第一个任务:给定样本集
回顾我们前面得到的公式:
(应用后验估计)
一维后验分布的性质
是关于 的二次函数的 函数,因此,也是一个正态分布密度函数。 被称为再生密度(reproducing density),因为对于任意数量的训练样本,当样本数量 增加时, 仍然保持正态分布。
由于
同时,我们也得到其公式为
进一步可解得:
这些方程展示了先验信息如何与样本中的经验信息相结合以获得后验密度
:代表在获得 个样本后对 的最佳猜测。 :衡量对 猜测的不确定性。 - 因为
随 单调递减,每增加一个观测值都将有助于减少我们对 真实值的不确定性。(这种先验起到了平滑的效果,导致了更加鲁棒的估计)
后验分布的变化趋势:因为
现在,我们希望获得后验数据分布 :
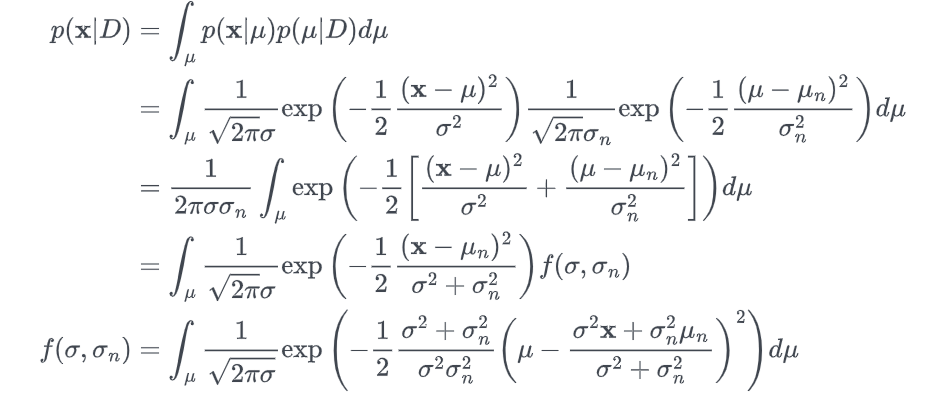
可以将
多元情形:高维
已知条件是:
参照上面一维的情况,可以推出:
数据后验分布服从正态分布:
贝叶斯学习
一般情形下的贝叶斯估计(总结)
基本假设:
密度
的形式已知,但参数向量的值未知。 关于
的初始知识包含在已知的先验密度 中。 关于
的其余知识包含在根据未知概率密度 独立抽取的 个样本 的集合 中。 基本问题:计算关于参数
的后验密度 和关于数据的后验密度 。
遇到的困难:
除了一些特殊的分布(共轭分布)之外,对于一般情形,积分很难计算:
参数先验
怎么选取?对结果有何影响? p(θ) 的选择对结果有直接影响。先验分布过于强烈可能会导致数据驱动的结果被先验主导,而过于弱的先验分布可能导致计算结果不稳定。
给定
,我们真的能通过 将 估计得很好吗?或者说,随着 中样本的增多, 收敛于 吗? 根据贝叶斯学习的性质,当数据量
时,后验分布 会集中在最大似然估计值附近,即: 这意味着后验分布的方差会逐渐缩小,预测分布 p(\mathbf{x}∣D)p(\mathbf{x}\vert D) 也会趋近于真实分布。
贝叶斯学习的迭代计算公式:
记
,由于样本是独立选样,则: 于是有如下迭代公式:
为统一表示,记参数先验分布
记
一般来说,随着样本数目的增加,上述序列函数逐渐尖锐,逐步趋向于以
例:贝叶斯估计
假设一维随机变量
基于先验知识,我们知道
迭代过程
在任何数据到达之前,我们有
当第一个数据点
其中忽略了归一化。因为
当第二个数据点
当第三个数据点
当第四个数据点
当数据点
关于参数
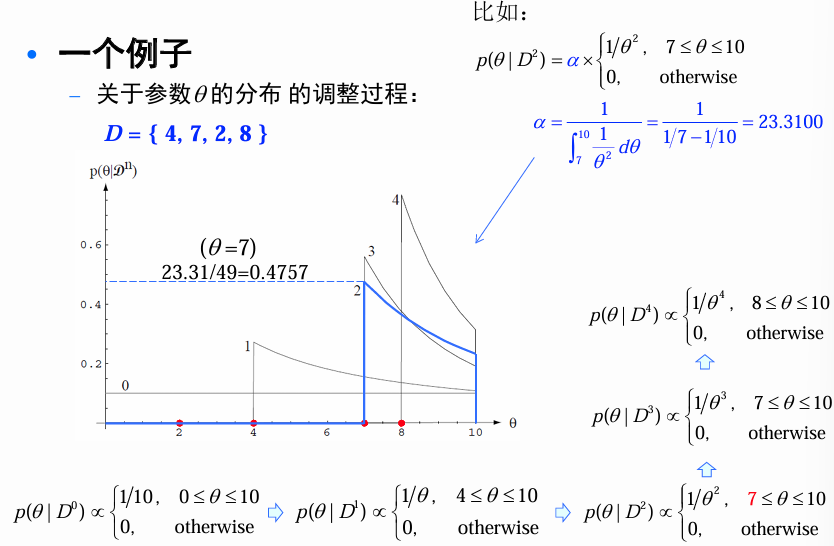
参数
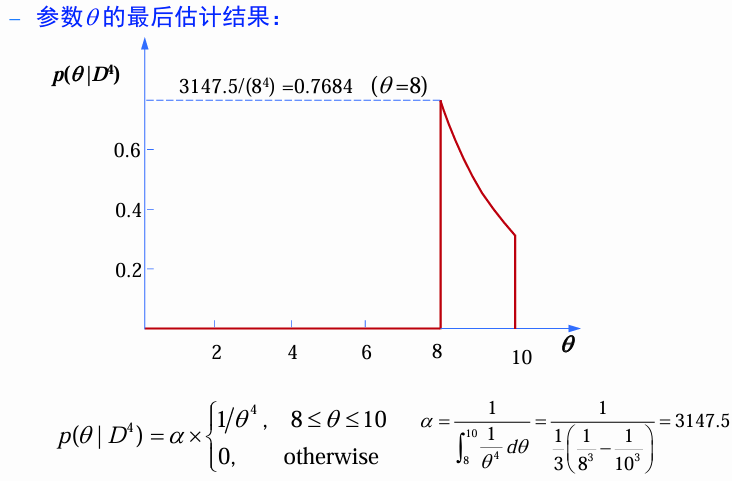
最后的分布:
最大似然估计做法
对于数据,其似然函数为:
显然,
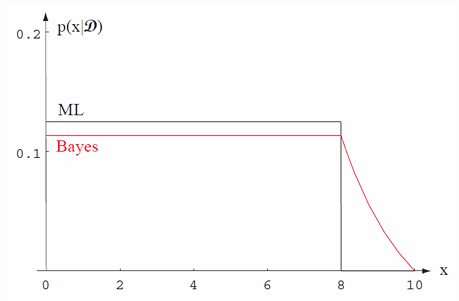
图中展示了最大似然估计(ML)和贝叶斯估计(Bayes)在样本后验分布上的区别。文中提到最大似然方法估计的是
特征维数问题:分类错误率与特征的关系
模式分类与特征的关系
- 贝叶斯决策(0-1损失):
- 特征空间给定时,贝叶斯分类错误率就确定了,即分类性能的理论上限就确定了(与分类器、学习算法无关)
增加特征有什么好处:判别性:类别间有差异的特征有助于分类
带来什么问题:泛化性能、Overfitting(过拟合)、计算、存储
高斯分布(两类问题)
Bayes error rate(贝叶斯错误率):
高斯分布(两类问题)
Conditionally independent case(条件独立情况)
一维的二类均值之间距离反映区分度,从而决定错误率。
特征增加有助于减小错误率(因为
增大)
特征维数决定可分性的例子 :
- 3D空间完全可分
- 2D和1D投影空间有重叠
然而,增加特征也可能导致分类性能更差,因为有模型估计误差(wrong model)
过拟合(Overfitting)
特征维数高、训练样本少导致模型参数估计不准确
比如协方差矩阵需要样本数在
以上.
图中展示了一个10阶多项式拟合的例子,函数为
,其中 ,虽然完美拟合训练数据,但测试误差很大.
克服办法
特征降维:特征提取(变换)、特征选择
参数共享/平滑
方法一:共享协方差矩阵
方法二:Shrinkage(a.k.a. Regularized Discriminant Analysis)第i类协方差矩阵给出需要分别使用第i类数据和所有数据计算
、属于启发式方法。
扩展:开放集分类的特征维数问题
开放集分类问题:
- 已知类别:
- 后验概率
无训练样本,测试样本作为outlier(异常值)拒识
特征维数问题:
- 区分
个类别比区分 个类别需要更多的特征 - 如果分类器训练时瞄准区分
个已知类别,测试时易造成outlier与已知类别样本的混淆 - 因此,在
类样本上训练分类器时,要使特征表达具有区分更多类别的能力 - 比如,训练神经网络时加入数据重构损失(类似auto-encoder)作为正则项,生成一些假想类样本(通过组合已知类别样本)
期望最大化 (Expectation-Maximization, EM)
引入
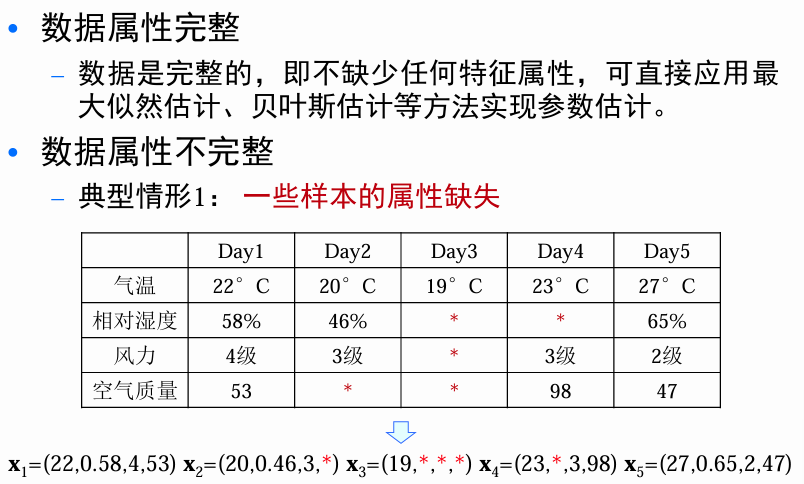

数据完整情况下例子
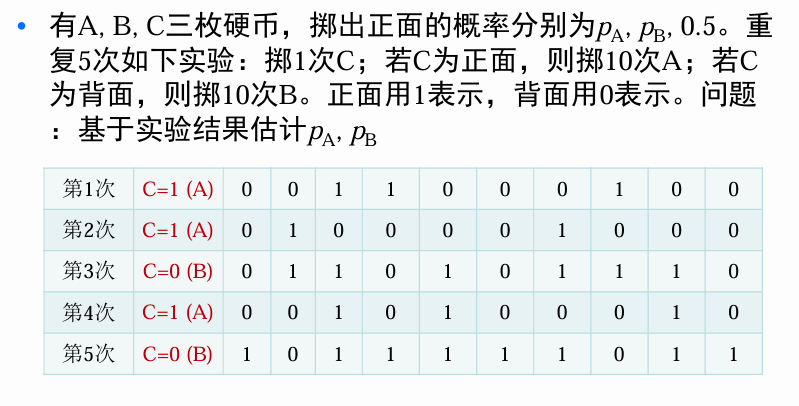
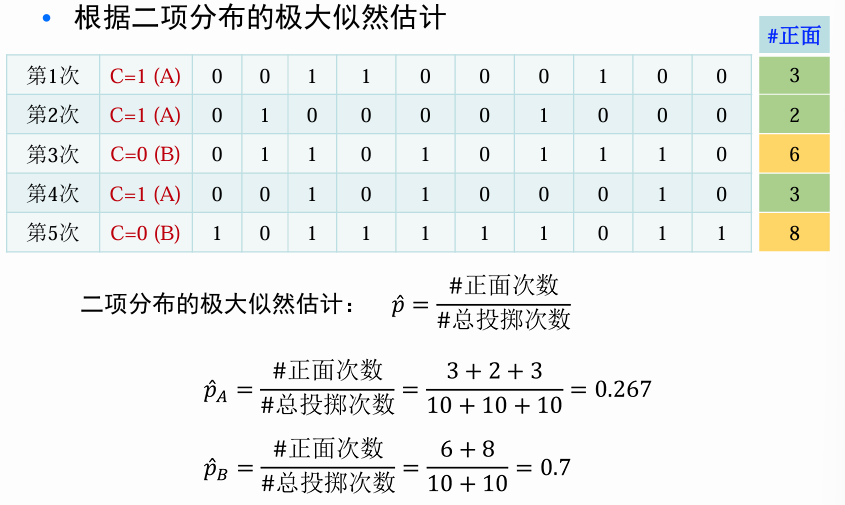
数据不完整情况下例子
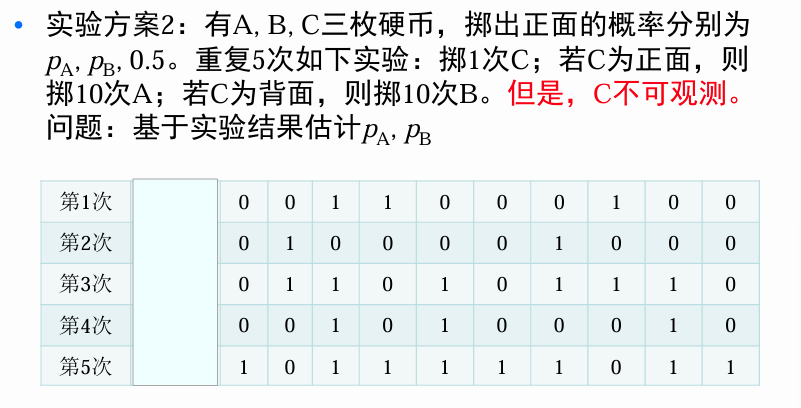
概率模型:


EM 算法求解
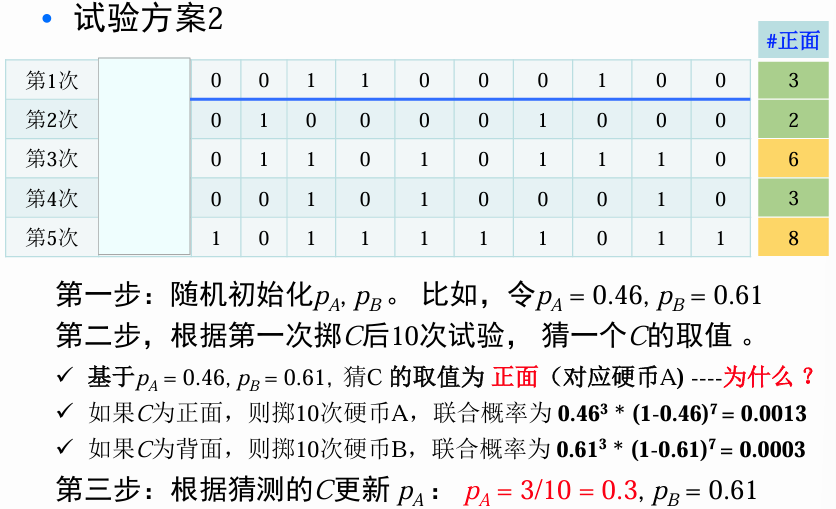
- 第四步:根据第二次掷硬币
后进行的10次试验,来猜测 的取值。 - 如果
为正面,那么掷10次硬币 ,其联合概率为 。 - 如果
为反面,那么掷10次硬币 ,其联合概率为 。 - 所以猜测
的取值为正面。
- 如果
- 第五步:根据猜测的
值来更新 和 的值: - 第六步:根据第三次掷硬币
后进行的10次试验,来猜测 的取值。 - 如果
为正面,那么掷10次硬币 ,其联合概率为 。 - 如果
为反面,那么掷10次硬币 ,其联合概率为 。 - 所以猜测
的取值为反面。
- 如果
- 第七步:根据猜测的
值来更新 和 的值: - - 第八步:根据第四次掷硬币
后进行的10次试验,来猜测 的取值。 - 如果
为正面,那么掷10次硬币 ,其联合概率为 。 - 如果
为反面,那么掷10次硬币 ,其联合概率为 。 - 所以猜测
的取值为正面。
- 如果
- 第九步:
- 第十步:根据第五次掷硬币
后进行的10次试验,来猜测 的取值。 - 如果
为正面,那么掷10次硬币 ,其联合概率为 。 - 如果
为反面,那么掷10次硬币 ,其联合概率为 。 -所以猜测 的取值为反面。
- 如果
- 第十一步:
一般情况
EM是一类通过迭代实现参数估计的优化算法: 作为最大似然法的替代,用于对包含隐变量(latent variable)或缺失数据(incomplete-data)的概率模型进行参数估计。
EM 算法的核心思想是:
- E 步(Expectation):计算隐变量的期望。
- M 步(Maximization):最大化对数似然,更新参数。
EM算法解决的问题:包含隐变量的概率密度参数估计
- 观测变量:
;隐含变量: - 任务:给定数据集
,估计观测数据概率密度的参数
| EM算法基本要素 | 公式 |
|---|---|
| 观测数据 | |
| 隐含数据 | |
| 观测数据的概率密度函数 | |
| 完全数据的联合概率密度函数 | |
| 观测数据的对数似然函数 | |
| 完全数据的对数似然函数 |
算法步骤
| 算法步骤 | 对应公式 |
|---|---|
| 1. 初始化 | |
| 2. (迭代)E步 | 基于当前 |
| 3.(迭代)M步 | 基于当前所估计的 |
| 4.(迭代) t=t+1 | 回到E步,开始迭代 |
另一种等价表述
初始化:
重复以下步骤:
- E步(E step):基于当前
和样本,估计隐变量的后验分布 ,并计算 :
- E步(E step):基于当前
M步(M step):更新参数
: 更新时间步:
EM for Gaussian Mixture
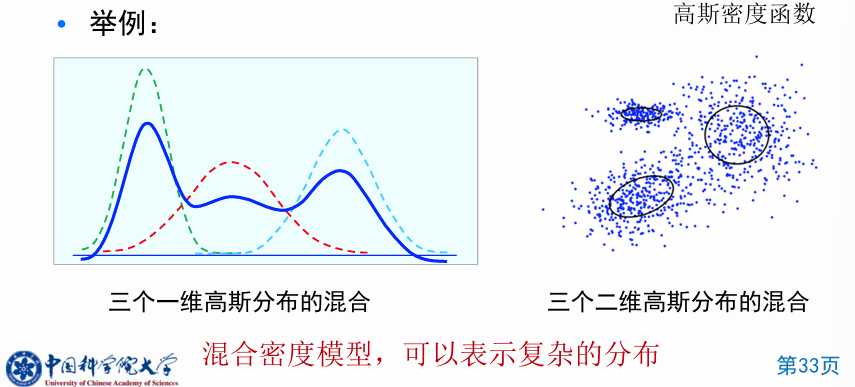
混合密度模型:由
| 混合密度模型 | 说明 |
|---|---|
| 权重条件 | 每个成分的权重为 |
| 概率密度函数 | 每个成分的概率密度函数为 |
| 混合密度模型公式 | |
| 混合密度模型的参数估计 | 已知样本集 |
高斯混合模型(Gaussian Mixture Model,GMM)
GMM: 成分密度为高斯密度的混合模型=高斯混合模型。
其中
- 权重参数:
- 成分参数:
, ( )
参数估计:最大似然(Maximum Likelihood,ML)
(可通过梯度下降迭代求解,但不能解析求解)
Q: 解析解?
A: 解析求解是指通过数学推导和公式运算,直接得到问题的精确解。在参数估计中,如果能够解析求解,就意味着可以通过一系列的代数运算和推导,得到模型参数的精确表达式。因此只能使用梯度下降这样的迭代算法来逐步逼近最优解。
引入隐变量分析混合密度模型
引入隐变量
| 引入隐变量 | 公式 |
|---|---|
| 假设条件 | |
| 观测变量 |
|
| 观测变量 |
因此,可以将混合密度模型看成包含隐变量
EM算法估计参数
不完全数据
,完全数据 :Missing the latent value z\in\{1,2,\cdots,K\}$。 完全数据对数似然期望:
- 选择初始参数集
- 执行以下操作
- E-step:计算
。 - M-step:更新参数:
。 - 如果收敛条件不满足:
- E-step:计算
- 结束
- 选择初始参数集
E步(E-Step):固定当前估计的参数
,对每个样本求 , 。( ) M步(M-Step):固定
,通过 更新参数 。 | 成分 | 对应公式 |
| ——————————————— | —————————————————————————————— |
| 成分权重| |
| 成分均值| |
| 成分协方差矩阵| | 记录所有的未知参数, 所以要迭代: 在极端情况下,即当样本
来自于一个成分时,其后验概率 ,否则就为零,此时有: 上标
表示属于第 个成分的样本, 表示属于第 个成分样本总数。 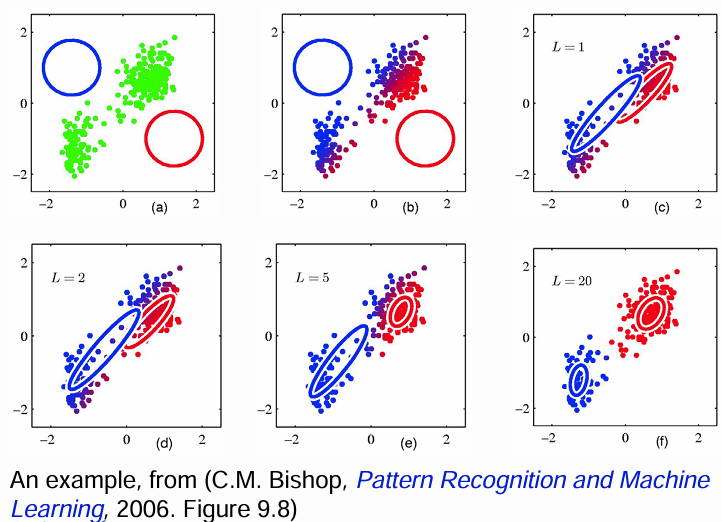
EM:数据缺失情况下的参数估计
对缺失数据求期望:
- 初始化
- E 步(期望步骤):
- 用已有的参数
预测缺失数据可能的取值(隐变量(缺失数据)的期望)。
- 用已有的参数
- M 步(最大化步骤):
- 利用完整的数据(观测数据和填补的缺失数据)重新估计参数。
- 交替迭代 E 步和 M 步,直到收敛(即参数的变化很小或者对数似然函数几乎不再增加)。
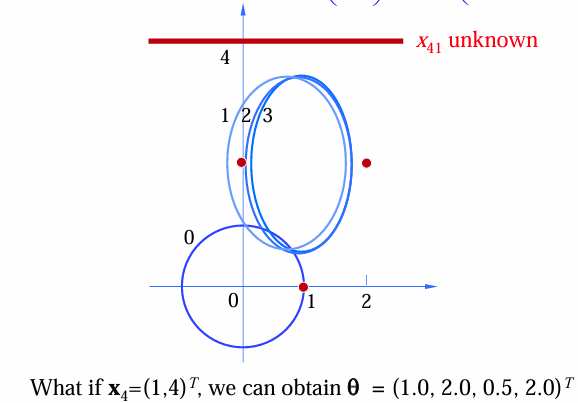
例:2-D高斯EM
数据集
是 2D 高斯分布的一部分,其中有一个样本 x4x_4 的第一个维度 缺失(用 * 表示)。 高斯分布的参数为
,即两维数据的均值和方差。 我们的目标是:在部分数据缺失的情况下,通过迭代的方法估计参数
。 挑战:缺失数据
使得直接用最大似然估计参数变得困难,需要引入 EM 算法
EM算法步骤
初始化参数为
。 E 步:计算缺失数据的期望:第四个样本
,假设其分布为: 根据条件高斯分布公式,计算 的条件分布,然后求期望值和相关的加权概率。 M 步:最大化对数似然
重复 E 步和 M 步: 迭代 3 次后,收敛到:
EM算法的理论解释

对任意分布
KL距离(KL散度):也称KL散度,衡量相同事件空间中两个概率分布之间的差异。KL距离恒大于等于零;当且仅当
时,有 。 因为KL距离恒大于等于零,因此
是 的下界,当且仅当 时,有 .
令
E步(E Step):固定
,最大化 M步(M Step):固定
,最大化
因此,EM是在通过坐标轮替法最大化
隐马尔可夫模型(HMM)
时间序列模型:
是序列长度 是 在t时刻的观察数据 - 不满足独立假设、观测数据间具有很强的相关性。
Q: 如何对序列数据表示、学习和推理?
首先需要引入关于数据分布和时间轴依赖关系的概率模型,即如何表示
对
- 方法1具有极强的灵活性、通用性,但参数量大、计算复杂度高
- 方法2具有极差的灵活性、通用性,但参数量小、计算复杂度低
- 如何平衡灵活性和复杂度?
| 方法 | 联合分布 |
|---|---|
| 方法1:不对数据做任何独立性假设,直接对条件分布建模( |
|
| 方法2:假设 |
|
| 方法3:(Markov性) |
HMM的表示
Markov链
静态、离散、一阶Markov链的联合分布:
| 参数 | 说明 |
|---|---|
| 离散马氏链 | |
| 静态马氏链 | 转移概率 |
| 初始状态分布 | |
| 状态转移概率 |

例子
- 初始状态分布:
- 状态转移概率:
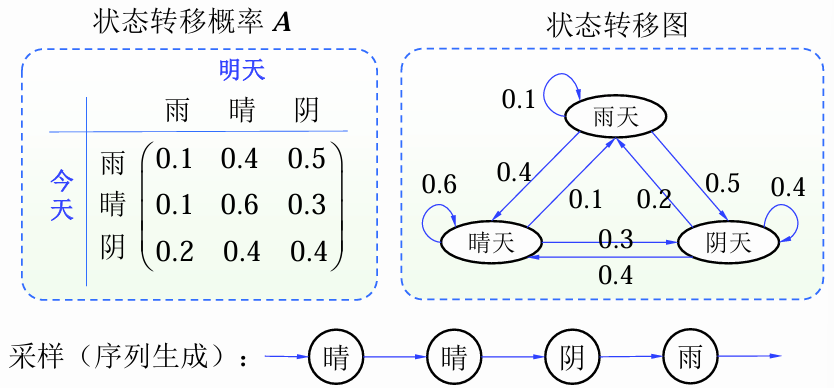
已知第
HMM简介
- HMM的基本思想
- 观测序列由一个不可见的马尔可夫链生成。
- HMM的随机变量可分为两组:
- 状态变量
:构成一阶、离散、静态马尔可夫链。用于描述系统内部的状态变化,通常是隐藏的,不可被观测的。其中, 表示第 时刻系统的状态。 - 观测变量
:其中, 表示第 时刻的观测变量,通过条件概率 由状态变量 生成;根据具体问题, 可以是离散或连续,一维或多维。
- 状态变量
- 主要用于时序数据建模,在CV、NLP、语音识别中有诸多应用。
HMM的图结构
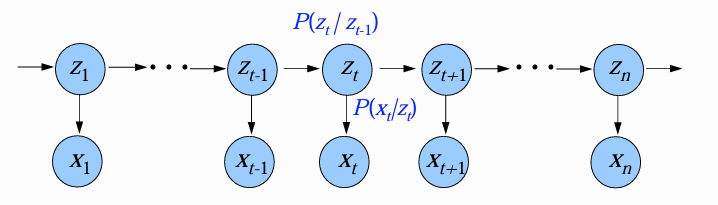
- 在图中,箭头表示依赖关系。
时刻的观测变量 的取值仅依赖于状态变量 。当 已知, 与其它状态独立。 时刻的状态变量 的取值仅依赖于 时刻的状态变量 。当 已知, 与其余 个状态独立。即 构成马尔可夫链,系统下一刻的状态仅由当前状态决定,不依赖于以往任何状态。
HMM中的条件独立性:
HMM联合概率分布:
| 基本要素 | 对应公式 |
|---|---|
| 初始状态概率向量 |
|
| 状态转移概率矩阵 |
|
| 发射概率矩阵 |
离散: |
例子
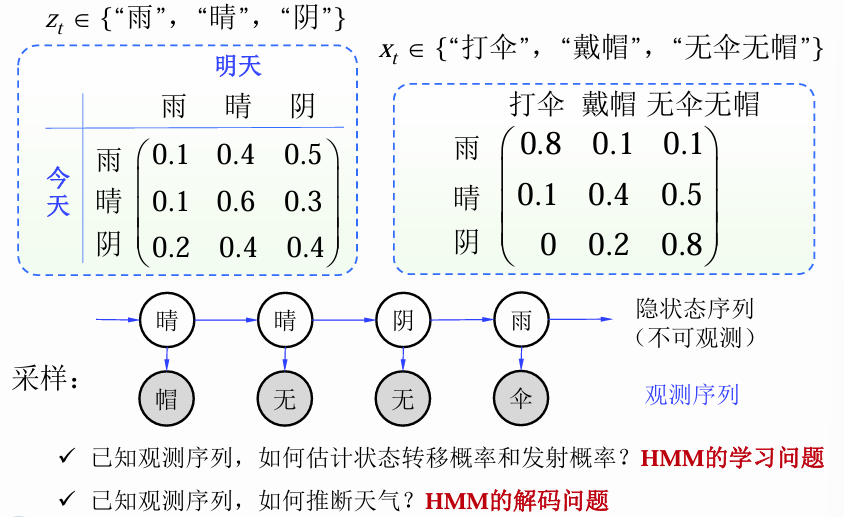
HMM的学习
三个基本问题
| 三个基本问题 | 简述 | 说明 |
|---|---|---|
| 给定模型 |
评估模型与观测数据的匹配程度。 | 许多任务需要根据以往的观测序列来预测当前时刻最有可能的观测值。 |
| 给定模型 |
根据观测序列推断出隐藏的模型状态。(解码问题) | 在语言识别中,观测值为语音信号,隐藏状态为文字,目标就是观测信号推断最有可能的状态。 |
| 给定观测序列 |
如何模型使其能够最好地描述观测数据。(参数估计-学习问题) | 在大多数实际应用中,人工指定参数已变得不可行,需要根据训练样本学习最优模型。 |
参数学习的基本任务
通过拟合观测序列,确定HMM中的参数:
EM算法步骤:
- E Step: 对给定的
,估计: - M Step: 用估计出的
,更新 : - E步和M步迭代运行,直至收敛
M step: 更新
用拉格朗日乘子法优化以下问题,可得:
| 参数 | 计算 | 约束 | 结果 |
|---|---|---|---|
E Step: 对给定的
只需估计:
以下省略
前向-后向算法(forward-backward algorithm)
- 前向概率:
- 后向概率:
- 观测概率:
从前向后计算,
从后向前计算,
HMM的解码
- 在实际问题中,状态变量通常有明确的含义。如语音识别中,
表示语音信号 对应的文本。因此,经常需要根据观测序列推断状态序列。 - 对给定的HMM模型
和观测序列 ,求解: 是最大后验概率对应的状态序列,也称为最优状态路径。 - 这对应分类问题中的最大后验概率决策,
对应 的类别。 - 与分类中对
独立解码不同,HMM需要联合解码。
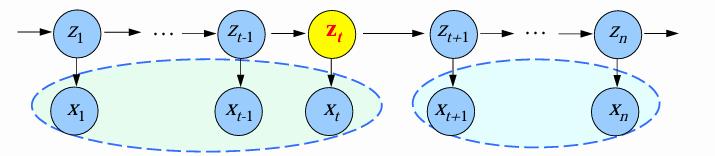
状态路径:
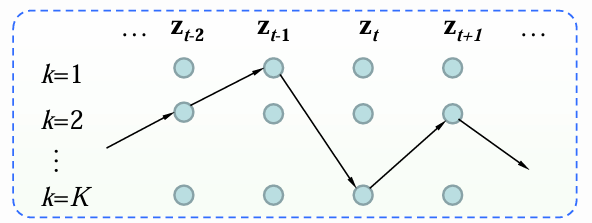
- 对于给定的HMM模型和观测序列
,不同状态路径对应不同的后验概率: 。 - 共有
条可能的状态路径,对应 个概率值。 - 直接计算这些概率,然后选出
的复杂度为 。
HMM的解码算法:维特比算法(Viterbi, 1967)
最优子问题:寻找以状态
结束的前 步最优状态路径 动态规划算法
- For
: - For
: - For
:
- For
- For
计算复杂度: