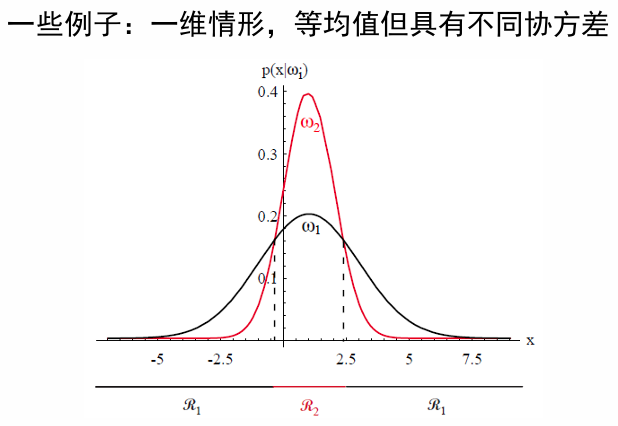
模式识别-Ch2-贝叶斯决策
Ch2 贝叶斯决策(Bayesian Decision Theory)
: 表示概率分布函数, : 表示概率密度函数PDF.
是 关于 的似然函数,表明在其他条件都相等的情况下,使得 较大的 更有可能是真实类别。(likelihood)
| 最小错误率贝叶斯决策 | 最小风险贝叶斯决策 | |
|---|---|---|
| 目标 | 使分类的错误率最小。 | 使决策的风险最小。 |
| — | 只考虑了错误分类的概率。 | 考虑了不同类型错误的代价。 |
| 将 |
衡量当样本实际属于某类但被决策 |
最小错误率bayes决策
任务:对于观测样本
| 已知 | 公式表达 | |
|---|---|---|
| 类别 | ||
| 特征向量 | ||
| 先验概率 | ||
| 条件概率/PDF | $p(\mathbf{x} | w_i)$ |
贝叶斯决策:
后验概率:
决策规则:如果
, 则 其他等价形式:
则
, 否则
例子
假设在某个局部地区细胞中正常(
解:因为
最小风险bayes决策
- 风险是和损失关联在一起的。
- 决策/行为:采取的决定。
- 决策/行为空间:所有可能采取的各种决策组成的集合。
- 每个决策/行为都会带来损失,损失是决策和自然状态(类别)的函数。
任务:对于观测样本
| 已知 | 公式表达 | |
|---|---|---|
| 类别 | ||
| 特征向量 | ||
| 先验概率 | ||
| 条件概率/PDF | $p(\mathbf{x} | w_i)$ |
| 决策空间 | ||
| 损失函数 | $\lambda(\alpha_i | w_j)$ |
损失函数:表示当类别为
时所采取的决策 所引起的损失,简记为 .

那么我们将做出决策
条件风险:条件期望风险
表示的是 实际类别为 时的概率,再乘以现在做出了 决策对应的损失函数, 对应 做了决策 的损失。
期望风险(总风险):将决策规则视为随机变量
| - | 期望风险 |
条件风险$R(\alpha_i | \mathbf{x})$ |
|---|---|---|---|
| 反映对整个特征空间上所有样本所采取的相应决策所带来的平均风险. | 只反映对样本 |
||
| 区别 | 理论推导 | 实际操作 | |
| 决策规则 | 最小化期望风险 |
在各中决策中选择风险最小的决策$a=\arg\min_{j=1,\dots,a}R(\alpha_j | \mathbf{x})$ |
c=2且无拒识
假设没有拒识(分类器拒绝分类, 当最大后验不高(置信低), 可能是不可分的情况)(
决策规则:

其他等价形式:
不失一般性,可以假设
, ,于是有:
- 若
,则 ;否则 - 若
,则 ;否则 - 若
,则 ;否则
例: 最小风险bayes决策
假设在某个局部地区细胞中正常
解: 前面已经解得
进一步计算条件风险:
由于
条件风险是0-1损失
假如条件风险是0-1损失,则有:
那么最小错误决策、最大后验(MAP):
若对于所有
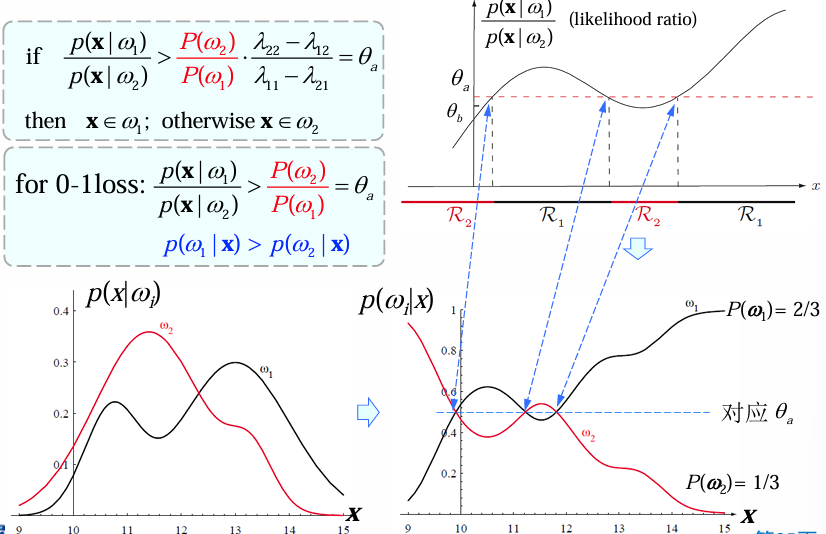
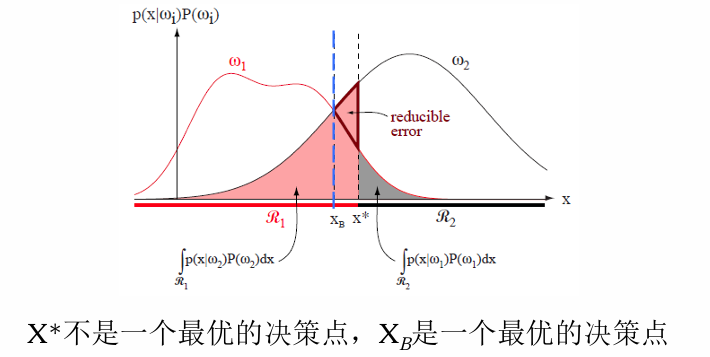
此图给出了决策规则+
+似然比 . 存在一个问题:当
时如何决策?引入带拒识的决策。
c=c+1且带拒识
Q: why 拒识?
错误识别可能带来严重后果。
Q: 是否每次一定要做出决策?
在有的情况下,不做决策比做出错误率很大的决策会更好。
具有c + 1个类别(分类器可以拒绝将样本判为c个类别中的任何一类)
假设:
风险:
当
因此有以下决策规则:
开放集分类bayes决策
传统的分类器:假设训练样本和测试样本都来自预设的C个类别(闭合集, Closed set)。
开放集(Open set):实际环境中,测试样本可能不属于预设的C个类别(异常样本, outlier)。
开放集的难点是异常样本没有训练集,只能训练已知C类的分类器。
问题表示
| 已知 | 公式 | ||
|---|---|---|---|
| 类别 | |||
| 先验概率 | |||
| 后验概率 | $\sum_{i = 1}^{c} P(w_i | \mathbf{x})\le 1,\ \sum^{c+1}_{j=0}P(w_i | \mathbf{x})=1$ |
| 条件概率密度 | $p(\mathbf{x} | w_i), (i = 1, \ldots, c)\ p(\mathbf{x} | w_{c + 1}) =?$ |
分类决策
假设:
后验概率:
最大后验概率决策:
分类器设计

判别函数
用于表达决策规则的某些函数称为判别函数。
通常定义一组判别函数
如果
参照贝叶斯决策规则,我们可以定义:
c=2情形下的判别函数
对于两类情形,只需要定义一个判别函数:
决策面
对于
各决策域
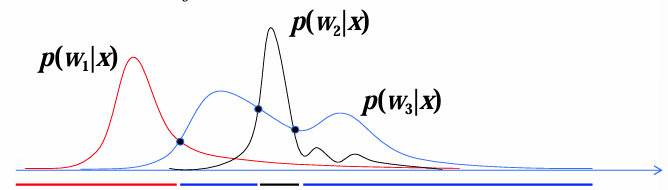
c=2情形下的决策面方程
为一维时,决策面为一些分界点;二维时,决策面为一些曲线(曲线段);三维时,决策面为一些曲面(曲面片);高维时则为一些超曲面(超曲面片)。 - 若
为线性判别函数,则为平面或平面片。
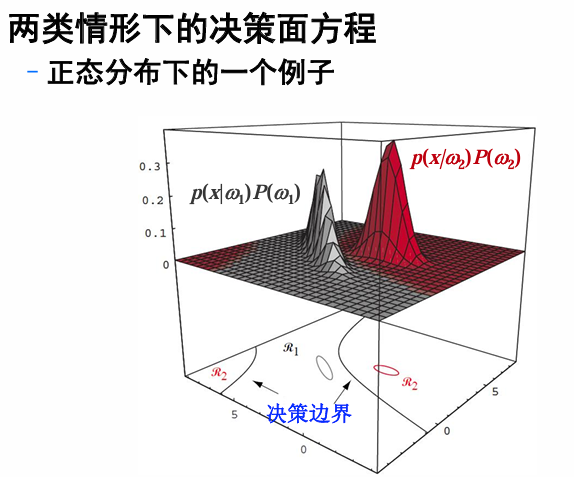
分类器设计
分类器可以看成一个机器,其功能是计算出 c 个判别函数,然后再从中选出对应于判别函数为最大值的类 作为分类结果。
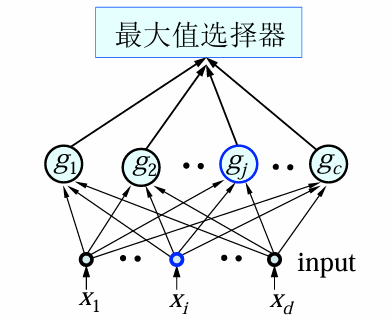
高斯密度下的判别函数
高斯分布
- 在给定均值和方差的所有分布中,正态分布的熵最大
- 根据Central Limit Theorem(中心极限定理),大量独立随机变量之和趋近正态分布
- 实际环境中,很多类别的特征分布趋近正态分布
多元正态分布:
: 边际分布密度函数:
| 单变量正态分布 | 多元正态分布 | |||
|---|---|---|---|---|
| 密度函数 | $p(\mathbf{x}) = \frac{1}{(2\pi)^{d/2} \ | \boldsymbol{\Sigma} | ^{1/2}} \exp \left( - \frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu}) \right)$ | |
| 均值 | ||||
| 方差 | ||||
| 性质 |
等密度轨迹
等密度轨迹为一超椭球面。从多元正态分布函数可以看出,当其指数项等于常数时,密度
Mahalanobis距离(马氏距离):
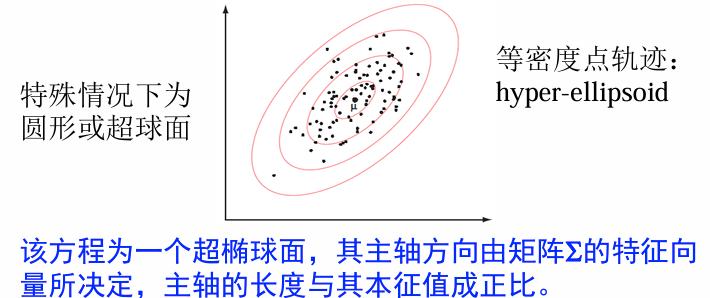
性质
不相关性=独立性
边缘分布与条件分布均为正态分布
多元正态随机变量的线性变换(非奇异)仍为多元正态分布的随机变量
线性组合的正态性:若
对多元正态分布的协方差矩阵
线性变换
白化变换:对
最小错误率贝叶斯决策
对于
判别函数(Quadratic discrimin function (QDF)):
决策面方程 :
第一种情形:
这表明每个特征向量对应的方差都是独立同分布。
协方差矩阵:
判别函数(Quadratic discrimin function (QDF)):
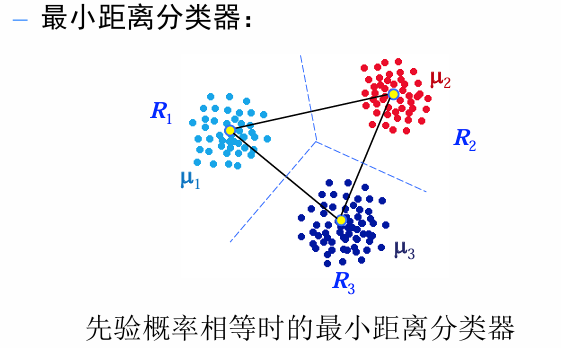
先验概率相等:
此时,判别函数可进一步简化为:
因此,最小错误率贝叶斯规则相当简单:
若要对样本
这种分类器称为最小距离分类器。
先验概率不相等:
判别函数:
由于每一类的判别函数均包含
决策规则: 若
判别函数为线性函数的分类器称为线性分类器。
线性分类器的决策面方程为:
| 先验概率相等
| —————————————————————————————— | —————————————————————————————— |
|
|
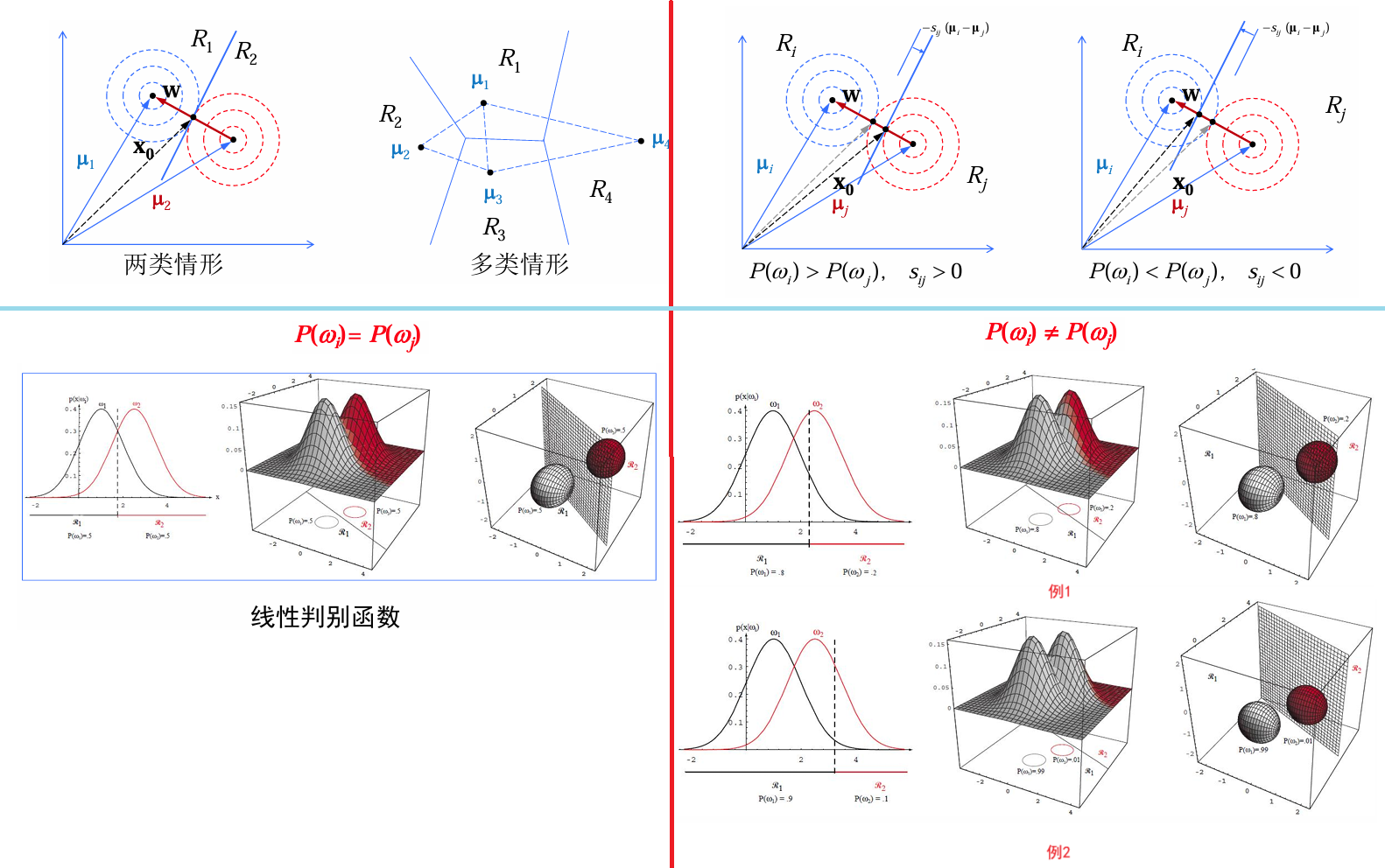
先验概率相等:取欧式距离的中点划分。
先验概率不等:根据
的大小会偏斜 先验概率较小的一边。
: 会向 偏. : 会向 偏.
第二种情形:
各类的协方差矩阵均相等。从几何上看,相当于各类样本集中于以该类均值
为中心但大小和形状相同的椭球内。
判别函数(Quadratic discriminant function (QDF)):
先验概率相等:
判别函数:
决策规则: 若要对样本
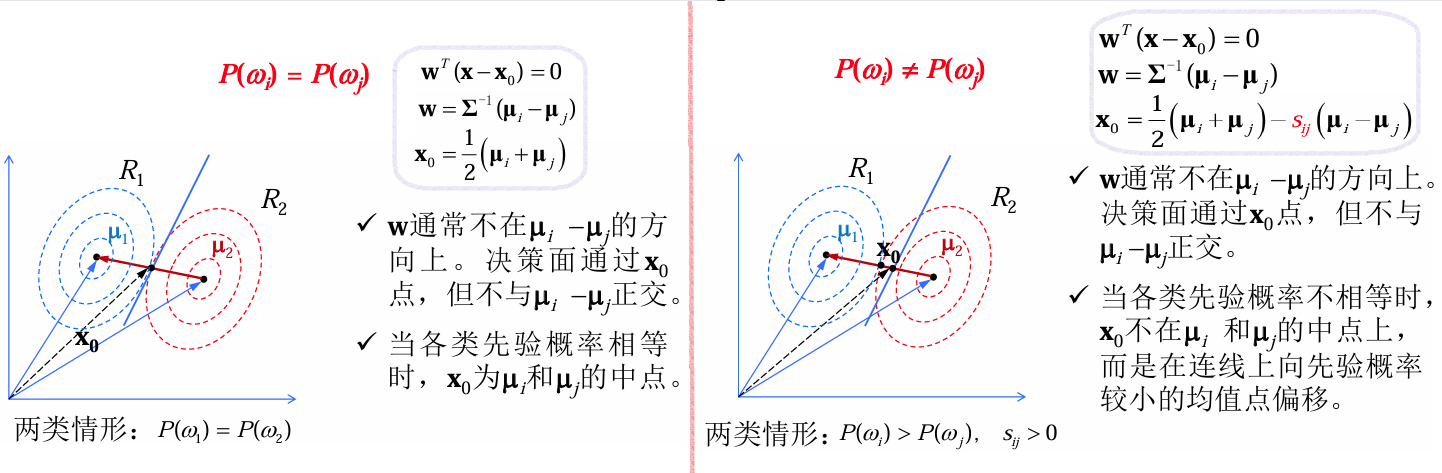
先验概率不相等:
判别函数:
决策面方程:
展开可得:
| 先验概率相等 |
先验概率不相等 |
||
|---|---|---|---|
| $\begin{align}\mathbf{x}_0&=\frac{1}{2}(\boldsymbol{\mu}_i+\boldsymbol{\mu}_j)-\frac{\sigma^2}{\ | \boldsymbol{\mu}_i-\boldsymbol{\mu}_j\ | ^2}\ln\left(\frac{P(w_i)}{P(w_j)}\right)(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j)\&=\frac{1}{2}(\boldsymbol{\mu}_i+\boldsymbol{\mu}_j)-s_{ij}(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j) \end{align}$ |
第三种情形:
判别函数:
决策方程:
决策面为一个超二次曲面。随着
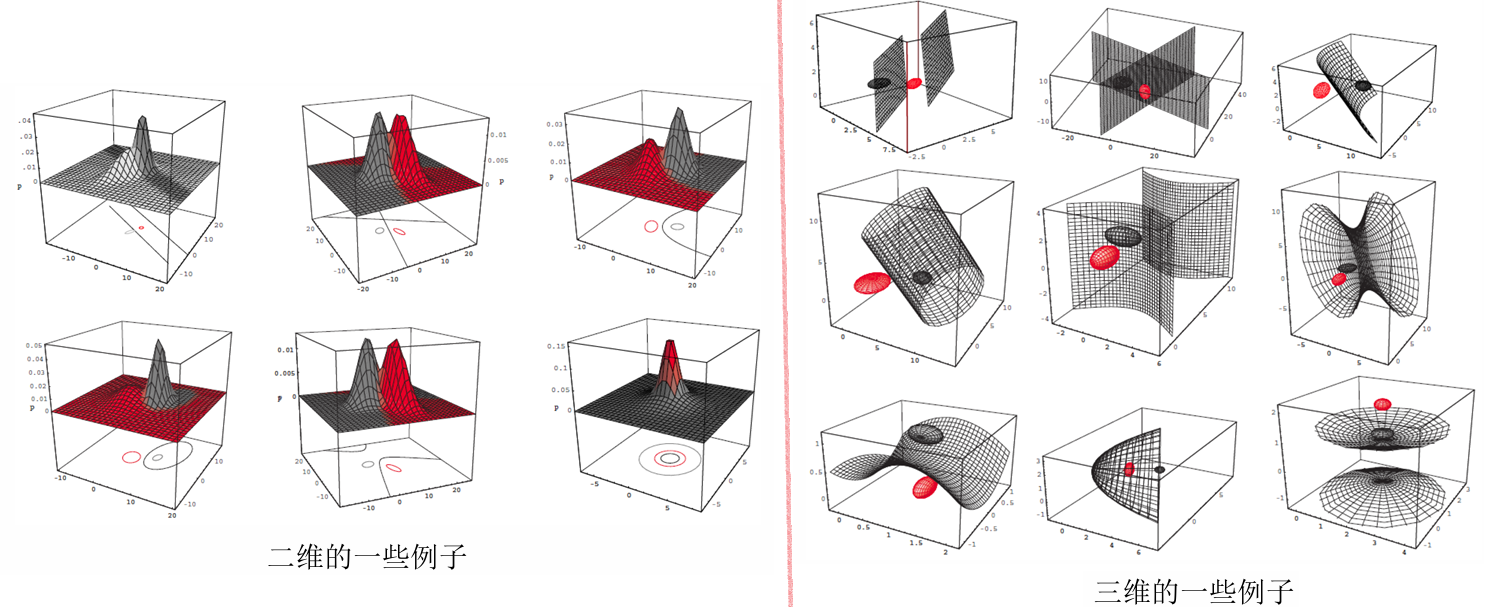
例子: c=2, 2D
对于两类问题,
决策面方程为
所以,此例子的决策面方程为
分类错误率
最小错误率贝叶斯决策
样本
样本
贝叶斯决策的错误率:贝叶斯决策的错误率定义为所有服从独立同分布的样本上的错误率的期望:
例:错误率(1D)
关于错误率,以一维为例说明: 考虑一个有关一维样本的两类分类问题。假设决策边界
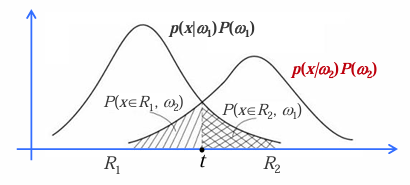
错误情形:样本在
考虑样本自身的分布后的平均错误率计算如下:
两类情形
平均错分概率:
例子
平均错分概率:
多类情形
平均错分概率:
平均分类精度:
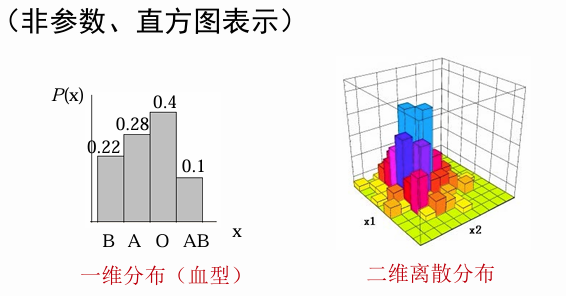
离散变量bayes决策
概率分布函数:
独立二值特征 (Binary features)
特征独立假设(Naïve Bayes):
每维特征服从伯努利分布(0/1分布)
| 在类别 |
在类别 |
||
|---|---|---|---|
| $p_i = P(X_{i}=1 | w_1),\quad i = 1,\ldots,d$ | $q_i = P(X_{i}=1 | w_2),\quad i = 1,\ldots,d$ |
| $P(\mathbf{x} | w_1)=\prod_{i = 1}^{d}p_i^{x_i}(1 - p_i)^{1 - x_i}$ | $P(\mathbf{x} | w_2)=\prod_{i = 1}^{d}q_i^{x_i}(1 - q_i)^{1 - x_i}$ |
似然比:
判别函数(QDF):
例子
例子是基于朴素贝叶斯分类器的二分类问题,并利用独立二值特征(Binary Features)推导出分类的决策边界
的过程。
已知:
例子
3D binary data -
复合模式分类(Compound Bayesian Decision Theory and Context)
多个样本同时分类
比如:字符串识别
贝叶斯决策:
其中:
注意:
选择后验概率最大的类别:
条件独立:在已知类别条件下,样本之间相互独立,即:
这种假设极大地简化了
先验假设(Prior assumption)
马尔可夫链(Markov chain)
- 先验概率可以表示为:
隐马尔可夫模型(Hidden Markov model,第 3 章介绍)
与复合模式识别类似的问题:多分类器融合
有同一个分类问题的
个分类器,对于样本 ,怎样使用 个分类结果得到最终分类结果? 一个分类器的输出:离散变量
多个分类器的决策当作样本
的多维特征,用Bayes方法重新分类: 需要估计离散空间的类条件概率 :指数级复杂度,需要大量样本
特征独立假设(Naïve Bayes)
总结
在已知类条件概率密度
- 单模式分类:连续特征、离散特征
- 复合模式分类
- 多分类器融合
贝叶斯分类器(基于贝叶斯决策的分类器)是最优的吗?
- 贝叶斯分类器是基于贝叶斯决策理论的分类器,其目标是最小化分类的总体风险(即误分类风险)。
- 最小风险:通过最小化条件风险(如 0-1 损失),选择最优分类。
- 最大后验概率决策 :在每个样本点
- 最优的条件:概率密度
- 具体的参数法(如正态分布假设)、非参数法(如 Parzen 窗、核密度估计)是贝叶斯分类器的近似,实际中难以达到最优。
- 判别模型(如逻辑回归、支持向量机 SVM):回避了概率密度估计,以较小复杂度估计后验概率
- 什么方法能胜过贝叶斯分类器:在不同的特征空间才有可能。
Q1: 贝叶斯分类器(基于贝叶斯决策的分类器)是最优的吗?
- 理论上:是的,贝叶斯分类器在理论上是最优的分类器,因为它最小化了分类风险。
- 实际中:不一定,因为贝叶斯分类器依赖于概率密度函数的精确估计,而实际中往往难以精确估计这些密度函数,特别是当数据分布复杂或高维时。
Q2: 什么方法能胜过贝叶斯分类器?
- 判别模型,如逻辑回归、SVM、神经网络等,特别是在以下情况下可能胜过贝叶斯分类器:
- 数据的真实分布复杂,难以准确建模。
- 特征空间高维,生成模型对概率估计的难度更大。
- 数据量有限时,生成模型容易过拟合。