图像处理-Ch4-图像复原

Ch4 图像复原

[TOC]

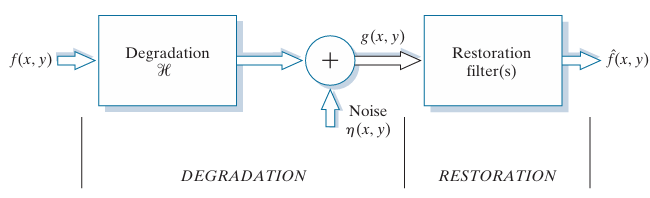
图像退化与复原(Image Degradation and Restoration)

图像复原目的：以某种预定义的方式改善给定图像。

Q: 图像增强 v.s. 图像复原?

A: 图像增强是一个主观的过程：自行选定不同的工具，比如低通、高通滤波，使得图像主观上看上去比较美观(因个人审美不同而不同)。

而图像复原的大部分过程是客观的。原先是什么样子、恢复原来的样子。

$$g(x,y)=H[f(x,y)]+\eta(x,y)\\ g(x,y)=h(x,y)*f(x,y)+\eta(x,y)\\ G(x,y)=H(u,v)F(u,v)+N(u,v)$$

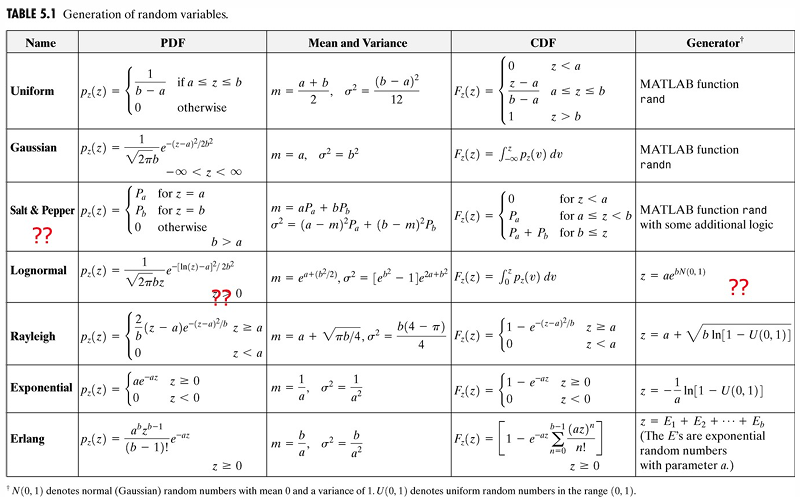
噪声模型(Noise Models)

假设:

i.i.d.空间随机噪声(Generating Spatial Random Noise with a Specified Distribution)

如果是在区间上均匀分布的随机变量，那么可以通过求解方程得到一个具有特定累积分布函数（CDF）的随机变量。

$$z = F_z^{-1}(w)$$

例：目标是生成具有瑞利（Rayleigh）累积分布函数（CDF）的随机数。

瑞利分布的累积分布函数（CDF）为:

$$F_z(z) = \begin{cases} 1 - e^{-(z - a)^2/b} & \text{if } z \geq a \\ 0 & \text{if } z < a \end{cases}$$

通过求解方程，可以得到的值：

$$z = a + \sqrt{-b \ln(1 - w)}$$

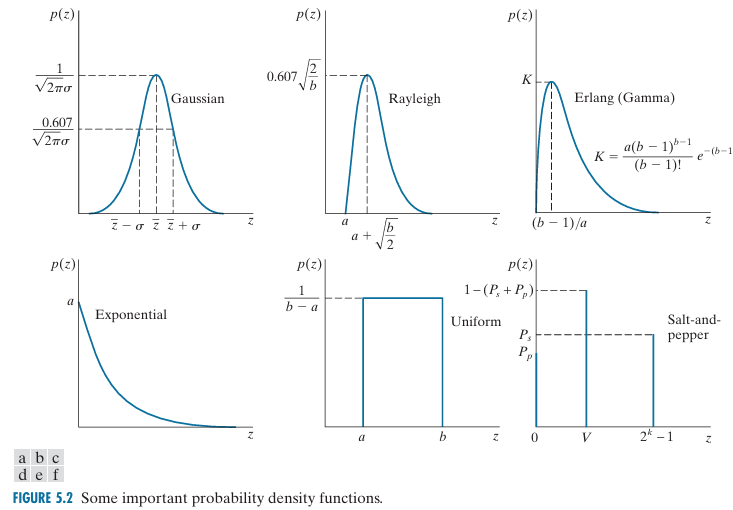
周期噪声(Periodic Noise)

在图像中，周期噪声是在图像获取时从电力或机电干扰中产生的。这是唯一一种空间依赖型噪声。

周期噪声信号(Periodic Noise Signal) ：

$$r(x, y) = A \sin(2\pi u_0(x + B_x)/M + 2\pi v_0(y + B_y)/N)$$

对于傅里叶变换：（实际上无法推出这个，但是大概是这个形式）

$$R(u, v) = \frac{A}{j2} \left[\exp\left(\frac{j2\pi u_0 B_x}{M}\right) \delta(u + u_0, v + v_0) - \exp\left(\frac{j2\pi v_0 B_y}{N}\right) \delta(u - u_0, v - v_0)\right]$$

估计噪声参数(Estimating Noise Parameters)

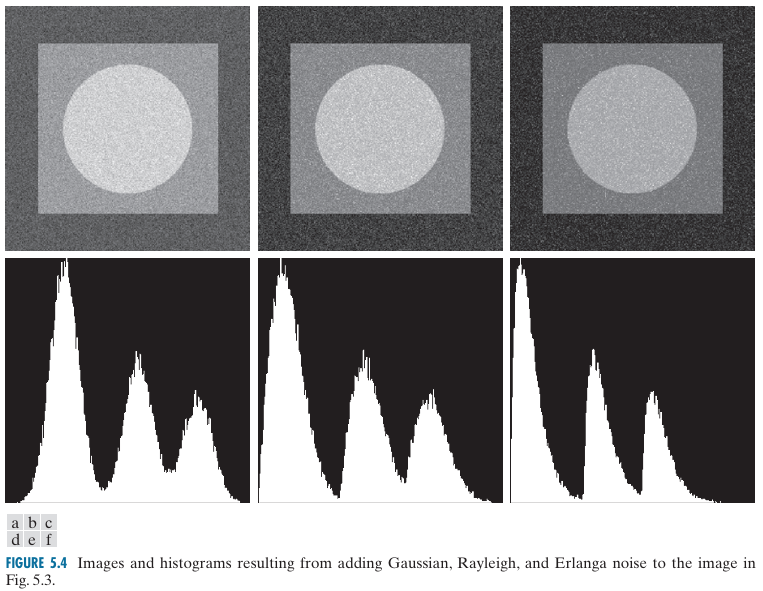
假如没有被噪声污染，那么图中有三个灰度级，直方图中应该有三根线。但是有噪声，现在每根线向两边扩展。

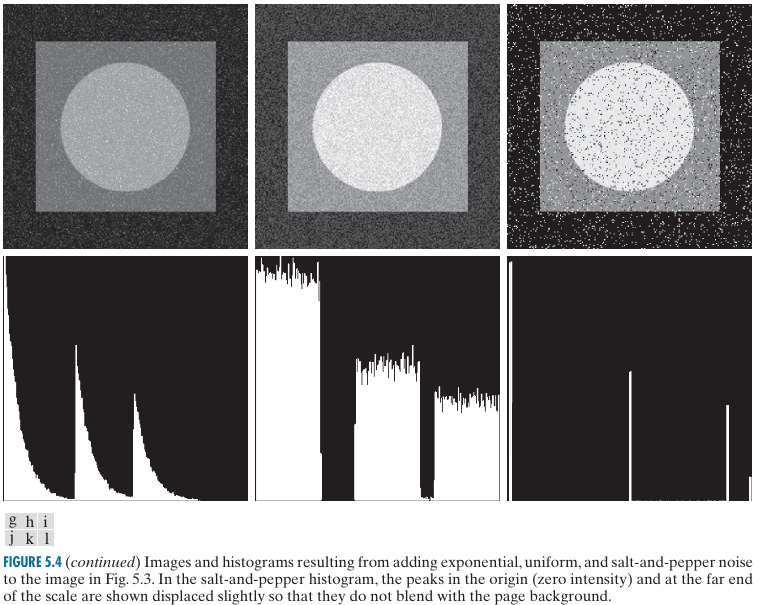
图l对应椒盐噪声的直方图：可以看见一共有4条线（两边分别有两条），椒盐噪声产生黑白、黑色估计和原有的背景色重合，于是直方图中最左的线特别的长（大概的解释）。

估计噪声参数：

1. 周期噪声：对图像的傅里叶谱审视，可以直接发现：比如在除中心的亮点之外，还有其他的亮点。

   

2. 具有先验知识：事先知道这种图像中会存在噪声、会出现在哪个频段。

3. 在平坦的图像区域，噪声会暴露出来：比如说一块纯色的地板，应该灰度级是差不多的。

Q: 怎么做？

1. 最简单的方法是利用图像中的采样数据来估计噪声的均值和方差。
2. 通过直方图的形状来辨识最接近的概率密度函数(PDF)的匹配。
3. 假如形状类似高斯，那么高斯只需要均值与方差。

统计矩与中心矩：

统计矩:

$$\mu_n = \sum_{i = 0}^{L - 1} (z_i - m)^n p(z_i) \quad \text{where} \quad m = \sum_{i = 0}^{L - 1} z_i p(z_i)$$

中心距：

n	对应中心距
0
1
2

在仅有噪声情况下图像复原-空域滤波

如果只有噪声, 图像退化模型可以表示为：

$$g(x,y)=f(x,y)+\eta(x,y)\\ G(u,v)=F(u,v)+N(u,v)$$

均值滤波器(Mean Filters)

均值相当于：给出一组数，经过一系列运算，得到一个新的值。这个值，比这组数中最小值大，比最大值小，那么调和均值滤波器、反调和均值滤波器就算均值滤波器。

滤波器	公式
算术平均滤波器
几何均值滤波器
调和均值滤波器
反调和均值滤波器

调和均值滤波器能够很好地去除盐噪声，但不能去除椒噪声。对于高斯噪声很好。

反调和均值滤波器非常适合消除椒盐噪声。当为正值时，该滤波器消除胡椒噪声。当为负值时，它消除盐噪声。它不能同时消除两种噪声。

• 当Q=0时：算术均值是反调和均值的一个特例。

  $$\hat y(x,y)= \frac{\sum_{(s,t) \in S_{xy}} g(s,t)}{\sum_{(s,t) \in S_{xy}}1}=\frac{1}{mn}\sum_{(s,t) \in S_{xy}}g(s,t)$$

• 当Q=-1时：是调和均值滤波器。

  $$\hat f(x,y)=\frac{\sum_{(s,t) \in S_{xy}1} }{\sum_{(s,t) \in S_{xy}}g(s,t)} =\frac{mn}{\sum_{(s,t) \in S_{xy}}g(s,t)}$$

统计排序滤波器(Order-statistics Filters)

椒盐噪声反复使用中值滤波器，总能完全去除；同时边缘信息也会丢失。

滤波器	公式
中值滤波器
中点滤波器
最大滤波器
最小滤波器
alpha均值滤波器

用频域滤波器消除周期噪声(Periodic Noise Reduction by Frequency Domain Filtering)

关于以下三种滤波器的奇妙比喻：来自王伟强老师。

入冬时存储的土豆，在开春时会发芽。

• 带阻滤波器：连皮肉带芽一起削掉。
• 带通滤波器：与带阻合为1体。
• 陷波滤波器：只把有芽的部分去除。

带阻滤波器(Bandreject Filters)

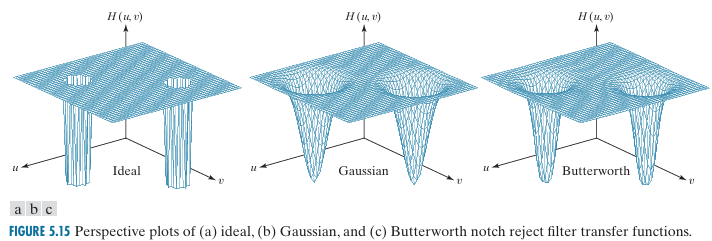
ideal	Gaussian	Butterworth
这里通常表示频率域中的距离，和是常数。这种滤波器是一种理想高通滤波器，它在频率域中完全截断了低频部分，保留了高频部分。	这里是滤波器的阶数。Butterworth高通滤波器是一种常用的滤波器，它在频率域中的响应是平滑过渡的，没有理想滤波器那样的尖锐截断。	Gaussian高通滤波器也是一种平滑过渡的滤波器，其形状基于高斯函数。
当频率距离小于或大于时，滤波器的响应为1，表示完全通过；当频率距离在和之间时，滤波器的响应为0，表示完全截断。	随着的增加，滤波器的响应从0逐渐增加到1，过渡的平滑程度由阶数决定。阶数越高，过渡越陡峭。	它的响应从0逐渐增加到1，过渡更加平滑，没有明显的截断点。

带通滤波器(Bandpass Filters)

$$H_{bp}=1-H_{br}(u,v)$$

带通滤波器执行与带阻滤波器相反的操作。得到噪声信号。

带通滤波器与带阻滤波器是一对儿；低通滤波器与高通滤波器是一对儿。

陷波滤波器(Notch filters)

成对出现。(a)是原图像，可以看见存在一些横纹(噪声)。然会得到(b)是(a)的傅里叶谱；通过(c)中的陷波滤波器的传递函数，可以去除掉噪声。(d)是图像复原后的图；(e)是提取出来的噪声。

Ideal	Gaussian	Butterworth
和是两个距离度量，是一个阈值。	它的过渡比Butterworth滤波器更平滑。	是滤波器的阶数。
当和都大于时，滤波器的传递函数值为1，表示完全通过；否则，传递函数值为0，表示完全截止。	这种滤波器基于高斯函数，传递函数的值从0逐渐增加到1。	随着和的增加，传递函数的值从0逐渐增加到1。阶数越高，过渡越陡峭。

公式中还定义了和的具体形式：

$$D_1(u, v)=\left[\left(u - \frac{M}{2} - u_0\right)^2+\left(v - \frac{N}{2} - v_0\right)^2\right]^{\frac 1 2}\\D_2(u, v)=\left[\left(u - \frac{M}{2}+u_0\right)^2+\left(v - \frac{N}{2}+v_0\right)^2\right]^{\frac 1 2}$$

这里和是图像的尺寸，和是滤波器的中心坐标。 这些高通滤波器在图像处理中常用于增强图像的高频细节，例如边缘和纹理。

不同的滤波器适用于不同的应用场景，第一种滤波器是理想高通滤波器，具有最尖锐的截止，但会导致振铃效应；Butterworth和Gaussian高通滤波器则提供了更平滑的过渡，减少了振铃效应。

最佳陷波滤波算法(Optimum Notch Filtering)

当存在多个干扰分量时，之前提到的方法并不总是可行的，因为在滤波过程中会去除过多的图像信息。这里讨论的方法是最优的，因为它使恢复估计值的局部方差最小化。

首先，通过以下方式获得噪声的初始估计：

$$N(u,v) = F_N(u,v)G(u,v)\\ \eta(x,y) = \mathfrak{J}^{-1}(F_N(u,v)G(u,v))$$

其中被构建为仅通过与干扰模式相关的分量。

令：

$$\hat{f}(x,y) = g(x,y) - w(x,y)\eta(x,y)$$

估计已知，我们将确定调制函数，以使的局部方差最小化。

目标：局部很好的平滑性，相邻的像素之间比较相似。

$$\min \sigma^2(x,y) = \frac{1}{(2a + 1)(2b + 1)} \sum_{s=-a}^{a} \sum_{t=-b}^{b} [\hat{f}(x + s, y + t) - \bar{f}]^2\\ \bar{f} = \frac{1}{(2a + 1)(2b + 1)} \sum_{s=-a}^{a} \sum_{t=-b}^{b} \hat{f}(x + s, y + t)$$

对上式展开：

$$\sigma^2 (x,y)= \frac{1}{(2a + 1)(2b + 1)} \sum_{s=-a}^{a} \sum_{t=-b}^{b} \\ \left[ [g(x + s, y + t) - w(x + s, y + t) \cdot \eta(x + s, y + t)] - [\overline{g(x,y)} - \overline{w(x,y)\eta(x,y)}] \right]^2$$

这个式子中只有是变量，变量一共有个变量。可以看到每一个位置都能建立这样的目标函数、有这么多的变量去求解，实在是难以计算。因此进行简化：将原来的M*N个位置的多目标优化问题，转化为了M*N个i.i.d,优化问题。

令, (将个变元简化为)我们有单变元函数：

$$\sigma^2(x,y) = \frac{1}{(2a + 1)(2b + 1)} \sum_{s=-a}^{a} \sum_{t=-b}^{b}\\ \left( [g(x + s, y + t) - w(x,y) \cdot \eta(x + s, y + t)] - [\overline{g(x,y)} - \overline{w(x,y)\eta(x,y)}] \right)^2$$

为了最小化，我们求解：

$$\begin{align}\frac{\partial \sigma^2}{\partial w(x,y)}& = 0\\ w(x,y) &= \frac{\overline{g(x,y)\eta(x,y)} - \bar{g}(x,y)\bar{\eta}(x,y)}{\overline{\eta^2}(x,y) - \bar{\eta}^2(x,y)} \end{align}$$

是平方的均值，是均值的平方。

这样我们就能求解出每个位置的weight: ，需要求M*N次。

估计退化函数(Estimating the Degradation Function)

该节分为以下两个部分进行讨论：

1. 假设没有噪声的情况：
2. 假设存在噪声的情况，如何处理？

进行图像复原，第一步要做的，就是找到. 有以下三种方法：

图像观察估计	实验估计	模型估计
设表示观测到的子图像，表示原始子图像的估计值，并且假设由于我们选择了强信号区域，噪声可以忽略不计，然后可以从推导出完整函数.		Hufnagel等人在1964年基于大气湍流的物理特性提出的退化模型. ,此时没有大气湍流，相应的，只有噪声影响了。
【一叶知秋】完全不知道图像是怎么获得的、只知道这副污染的图像.	我知道图像是被何设备何场景下拍摄、且我手里有这个设备、我再对特定的对象(平坦)在同样的条件下拍摄。用这个特殊对象来估计污染图像.	从高空拍摄地面，会受到气流的影响。

运动引起的图像模糊(Image Blur due to Motion)

现在，假设一幅图像由于均匀线性运动而变得模糊。

$$g(x,y) = \int_{0}^{T} f\left(x - x_0(t),y - y_0(t)\right) dt$$

是快门时间。然后，它的傅里叶变换是:

$$\begin{align*} G(u,v) &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} g(x,y) \exp\left[-j2\pi(ux + vy)\right] dxdy\\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} \left[\int_{0}^{T} f\left(x - x_0(t),y - y_0(t)\right) dt\right] \exp\left[-j2\pi(ux + vy)\right] dxdy\\ &= \int_{0}^{T} \left[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f\left(x - x_0(t),y - y_0(t)\right) \exp\left[-j2\pi(ux + vy)\right] dxdy\right] dt\\ &= \int_{0}^{T} F(u,v) \exp\left[-j2\pi(ux_0(t) + vy_0(t))\right] dt\\ &= F(u,v) \int_{0}^{T} \exp\left[-j2\pi(ux_0(t) + vy_0(t))\right]\\\\ H(u,v)& = \int_{0}^{T} \exp\left[-j2\pi(ux_0(t) + vy_0(t))\right] dt dt\end{align*}$$

如果，（垂直方向上没有发生运动，只是在水平方向上抖动了以下），那么：

$$H(u,v) = \int_{0}^{T} \exp\left(-j2\pi uat/T\right) dt = \frac{T}{\pi ua} \sin(\pi ua) \exp\left(-j\pi ua\right)$$

如果而不是0(水平、垂直方向上都发生了运动)，那么：

$$H(u,v) = \frac{T}{\pi(ua + vb)} \sin(\pi(ua + vb)) \exp\left(-j\pi(ua + vb)\right)$$

直接逆滤波(Direct Inverse Filtering)

对于被退化函数退化的图像，最简单的恢复方法是直接逆滤波:

$$\hat{F}(u,v) = \frac{G(u,v)}{H(u,v)}$$

可以看到，这个式子中假设，且我们需要已知.

那要是，我们可以得到:

$$\hat{F}(u,v) = F(u,v) + \frac{N(u,v)}{H(u,v)}$$

如果退化函数在某一个频率点有零值或非常小的值(一般都是离原点比较远的地方存在)，那么的比值会很大、可能会压制的估计，造成的估计存在较大误差。

一种解决方法是利用原点附近退化函数的值来进行逆滤波的计算。比如设置一个半径：，足够小的时候来计算; 的地方，做低通滤波。

(a)	(b)	(c)	(d)
这是使用完整滤波器（full filter）进行恢复的结果。	这是将滤波器函数在半径为 40 以外进行截断后进行恢复的结果。	这是将滤波器函数在半径为 70 以外进行截断后进行恢复的结果。	这是将滤波器函数在半径为 85 以外进行截断（cut off outside a radius of 85）后进行恢复的结果。
图像看起来较为模糊，细节不够清晰。	good	better	依托。

可以推断出来噪声的频率大于70.（85把噪声包含进去，此时就是的比值会很大、可能会压制的估计，造成的估计存在较大误差。得到了依托）

维纳滤波器(Wiener Filtering)

理论上最优的一种图像复原方法。

维纳滤波器寻求使统计误差函数最小化的估计值

$$e^2 = E\{(f - \hat{f})^2\}$$

是期望算子，是未退化图像。

此表达式在频域中的解为:

$$\hat{F}(u, v) = \left[\frac{1}{H(u, v)} \frac{|H(u, v)|^2}{|H(u, v)|^2 + S_n(u, v)/S_f(u, v)}\right] G(u, v)$$

其中 :

	$	H(u, v)	^2 = H^*(u, v)H(u, v)$		$S_n(u, v) =	N(u, v)	^2$	$S_f(u, v) =	F(u, v)	^2$
退化函数	—-	是的复共轭	是噪声的功率谱	未退化图像的功率谱

实际上很难在现实中求解：主要是因为、很难求噪声的功率谱以及未退化图像的功率谱。通常使用近似来应用：

$$\hat{F}(u, v) = \left[\frac{1}{H(u, v)} \frac{|H(u, v)|^2}{|H(u, v)|^2 + K}\right] G(u, v)$$

(a)(d)(g)原始图像	(b)(e)(h)逆滤波	(c)(f)(i)维纳滤波
原始的 8 位图像，受到了运动模糊和加性噪声的影响。	图像的模糊有所减少，但噪声被放大了。	与逆滤波相比，维纳滤波在减少模糊的同时，较好地抑制了噪声。
噪声方差降低了一个数量级。	—-	—-
噪声方差降低了五个数量级。	—-	通过降低噪声方差，维纳滤波能够有效地去除噪声并减少模糊。

约束最小二乘图像复原算法(Constrained Least Squares Filtering)

了解退化函数的问题 - 在本章讨论的所有方法中，都存在需要了解退化函数的问题。

维纳算法不好的是：得事先知道噪声功率谱和未退化图像谱，但这个很难知道。

接下来介绍约束最小二乘滤波方法，这个方法只需要知道噪声的均值和方差。

如果我们用矩阵来模拟退化过程，有：

$$g(x,y)=h(x,y)*f(x,y)+\eta(x,y) \\ g={H}{f}+{\eta}$$

将其转化成矩阵形式，相当于是做操作拉伸。比如原先的，现在的是.

该方法的核心是对噪声的敏感性问题。一种缓解该问题的方法是基于平滑度的度量进行恢复。

拉普拉斯（图像的二阶导数:）似乎是一个很好的选择。

一阶导反映变化快慢、二阶导反映了平滑程度。

需要最小化的代价函数为 :

$$\min C=\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}[\nabla^2 f(x,y)]^2\\ s.t.\ \|\mathbf{g}-\mathbf{H}\hat{\mathbf{f}}\|=\|\mathbf{\eta}\|$$

已知：。该问题在频域的解为 :

$$\hat{F}(u,v)=\left[\frac{H^*(u,v)}{|H(u,v)|^2+\gamma|P(u,v)|^2}\right]G(u,v)$$

其中是拉普拉斯算子在空域中的一个形式(傅里叶变换)。

$$P(x,y)=\begin{pmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{pmatrix}$$

令，且。

可以证明是的单调递增函数。因此，我们可以调整，使得 :

$$\|{r}\|^2=\|\mathbf{\eta}\|^2\pm\alpha$$

当足够小，那么. 回看频域的解：.

已知的条件有：,那么当确定时：

然后根据确定是否落入区间，不在区间的话，可以不断地调整,使落入邻域。此时，所估计的是问题的解。

Q: 前面假设噪声已知，那实际中如何计算？

$$\|\mathbf{\eta}\|^2 = MN[\sigma_{\eta}^2+m_{\eta}^2] \\\begin{cases}\sigma_{\eta}^2=\frac{1}{MN}\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}[\eta(x,y)-m_{\eta}]^2 \\ m_{\eta}=\frac{1}{MN}\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}\eta(x,y) \end{cases}$$

是噪声的方差和期望。

$$\begin{align*} \sigma_{\eta}^2&=\frac{1}{MN}\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}[\eta(x,y)-m_{\eta}]^2\\ &=\frac{1}{MN}\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}[\eta^2(x,y)-2m_{\eta}\eta(x,y)+m_{\eta}^2]\\ &=\frac{1}{MN}\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}\eta^2(x,y)-2m_{\eta}\frac{1}{MN}\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}\eta(x,y)+m_{\eta}^2\\ &=\frac{1}{MN}\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}\eta^2(x,y)-2m_{\eta}^2+m_{\eta}^2\\ &=\frac{1}{MN}\sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}\eta^2(x,y)-m_{\eta}^2 \\ \sum_{x = 0}^{M-1}\sum_{y = 0}^{N-1}\eta^2(x,y)&=MN[\sigma_{\eta}^2 + m_{\eta}^2]\\ \|\mathbf{\eta}\|^2 &= MN[\sigma_{\eta}^2+m_{\eta}^2] \end{align*}$$

下图都展示了经过约束最小二乘滤波处理后的图像。可以看到效果比维纳滤波好一点。