图像处理-Ch3-频率域增强

Ch3 频率域处理(Image Enhancement in Frequency Domain)

[TOC]

FT ：将信号表示成各种频率的正弦信号的线性组合。

频谱：

相位角：

功率谱：

• ： 的虚部。
• ： 的实部。

4.5 2-D Fourier Transform

4.5.1 2-D impulse

连续变量和的冲激函数定义为：

$$\delta(t,z)=\begin{cases} 1,\quad t=z=0\\ 0,\quad \text{其他} \end{cases}\\ \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(t,z)dtdz=1$$

取样性质：在冲激处产生函数的值。

$$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)\delta(t,z)dtdz=f(0,0)\\ \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)\delta(t-t_0,z-z_0)dtdz=f(t_0,z_0)$$

离散变量x和y，2-D离散冲激定义为(与连续冲激倒是定义一致，在冲激处值为1)：

$$\delta(x,y)\begin{cases} 1,\quad x=y=0\\ 0,\quad \text{其他} \end{cases}$$

取样性质：

$$\sum_{x=-\infty}^{\infty}\sum_{y=-\infty}^{\infty}f(x,y)\delta(x,y)=f(0,0)\\ \sum_{x=-\infty}^{\infty}\sum_{y=-\infty}^{\infty}f(x,y)\delta(x-x_0,y-y_0)=f(x_0,y_0)$$

==处理有限维图像时，上述两个公式的限制改为图像的维数。==

4.5.2 2-D Fourier Transform Pair(变换对)

2-D Fourier Transform：令是两个连续变量,的连续函数。

$$F(\mu,v)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)e^{-j2\pi(\mu t+vz)}dtdz\\ f(t,z)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(\mu,v)e^{j2\pi(\mu t+vz)}d\mu dv$$

是频率变量；是连续空间变量。定义了连续频率域。

二维盒式函数:

$$f(t,z)=\begin{cases} A,\quad -\frac T 2\le t\le\frac T 2,-\frac Z 2\le z\le \frac Z 2 \\ 0,\quad \text{其他} \end{cases}$$

对应的傅里叶变换如下：

$$F(\mu,v)&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)e^{-j2\pi(\mu t+vz)}dtdz\\ &=\int_{-\frac T 2}^{\frac T 2}\int_{-\frac Z 2}^{\frac Z 2}Ae^{-j2\pi(\mu t+vz)}dtdz\\ &=ATZ[\frac{sin(\pi\mu T)}{\pi\mu T}][\frac{sin(\pi v Z )}{\pi v Z}]$$

联系到一维情况下连续函数的情况：

$$f(t)&=\begin{cases} A,\quad -\frac{w}{2}\le t\le \frac{w}{2}\\ 0,\quad \text{其他} \end{cases}\\ F(\mu)&=\int_{-\infty}^{\infty}f(t)e^{-j2\pi\mu t}dt\\ &=\int_{-\frac w 2}^{\frac w 2}Ae^{-j2\pi\mu t}dt\\ &=-\frac{A}{2j\pi\mu}[e^{-j2\pi\mu t}]_{-\frac w 2}^{\frac w 2}\\ &=-\frac{A}{2j\pi\mu}(e^{-j\pi\mu w}-e^{j\pi\mu w})\\ &=\frac{A}{2j\pi\mu}(e^{j\pi\mu w}-e^{-j\pi\mu w})$$

因为,所以：

$$F(\mu)&=\frac{A}{\pi\mu}\sin(\pi\mu w)\\ &=Aw\frac{\sin(\pi\mu w)}{\pi\mu w}\\ &=Aw sinc(\pi\mu w)$$

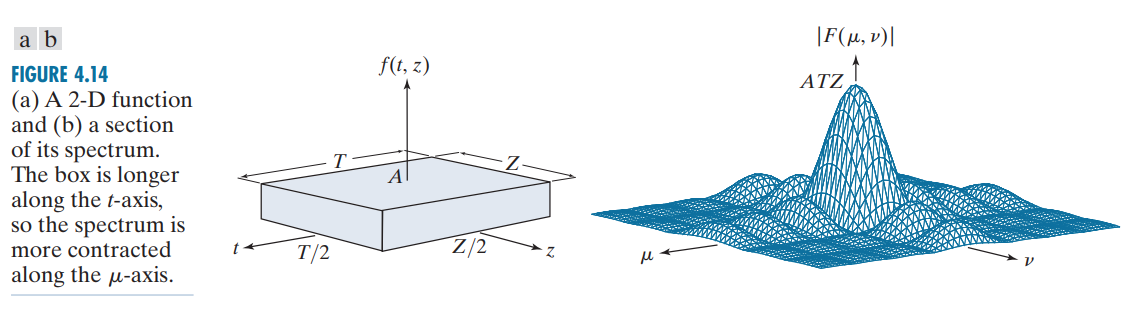
所以对于2-D情况下，更易理解。看下图：右图是频谱的一部分，谱中0位置与T,Z成反比，当，谱沿轴更“收缩”。

4.5.3 2-D Sampling

先介绍一下1-D sampling：

因为时域与频域对称：

$$\delta(t-t_0)\xrightarrow{\mathrm{FT}}e^{-j2\pi\mu t_0}, e^{-j2\pi\mu t_0}\xrightarrow{\mathrm{FT}}\delta(-\mu-t_0)=\delta(\mu+t_0)$$

冲激串：

$$S_{\Delta T}(t)=\sum^{\infty}_{k=-\infty}\delta(t-k\Delta T)=\sum^{\infty}_{n=-\infty}C_ne^{j\frac{2\pi n}{\Delta T}t}\\ C_n=\frac{1}{\Delta T}\int_{-\frac{\Delta T}{2}}^{\frac{\Delta T}{2}}S_{\Delta T}(t)e^{-j\frac{2\pi n}{\Delta T}t}dt$$

当t=0时产生冲激(区间内积分仅包含t=0处冲激)，此时:

$$S_{\Delta T}(t)=\sum^{\infty}_{n=-\infty}\frac{1}{\Delta T}e^{j\frac{2\pi n}{\Delta T}t}$$

对进行傅里叶变换：

$$S_{\Delta T}(t)\xrightarrow{\mathrm{FT}}\frac{1}{\Delta T}\sum_{n=-\infty}^{\infty}\delta(\mu-\frac{n}{\Delta T})\\ e^{\frac{j2\pi n}{\Delta T}t}\xrightarrow{\mathrm{FT}}\delta(\mu-\frac{n}{\Delta T})$$

对于2-D冲激串被定义为:

$$S_{\Delta T}(t,z)=\sum^{\infty}_{m=-\infty}\sum^{\infty}_{n=-\infty}\delta(t-m\Delta T,z-n\Delta Z)$$

是连续函数沿t轴和z轴的样本间的间隔。上式描述了沿两个轴无限扩展的一组周期冲激。

2-D带限函数：在建立的频率域矩阵外，：

$$F(\mu,v)=0, \quad |\mu|\ge\mu_{\max},|v|\ge v_{\max}$$

带限：当且仅当在两个坐标方向无限扩展的时候，一般才可能是带限的。

2-D取样定理：间隔满足or，则连续带限函数f(t,z)可由其一组样本无误地复原（无信息丢失）。

4.5.5 2-D DFT, IDFT

书上的形式:

$$\text{DFT:}\\ F(u,v)=\sum^{M-1}_{x=0}\sum^{N-1}_{y=0}f(x,y)e^{-j2\pi(\frac{ux}{M}+\frac{vy}{M})}\\ \text{IDFT}:\\ f(x,y)=\frac{1}{MN}\sum^{M-1}_{u=0}\sum^{N-1}_{v=0}F(u.v)e^{j2\pi(\frac{ux}{M}+\frac{vy}{M})}$$

PPT中给出的形式（此时这个常数的平方根应包含在正变换和反变换前面，以便形成一个更为对称的变换对）：

$$\text{DFT:}\\ F(u,v)=\frac{1}{MN}\sum^{M-1}_{x=0}\sum^{N-1}_{y=0}f(x,y)e^{-j2\pi(\frac{ux}{M}+\frac{vy}{M})}\\ \text{IDFT}:\\ f(x,y)=\sum^{M-1}_{u=0}\sum^{N-1}_{v=0}F(u.v)e^{j2\pi(\frac{ux}{M}+\frac{vy}{M})}$$

4.6 2-D DFT, IDFT的性质

• 空间间隔与频率间隔：与成反比。

  对连续函数取样生成了一副数字图像,它由t方向和z方向所取得个样本组成。令表示样本间的间隔。频率域对应的离散变量间的间隔分别为。

• 平移(shifting)：

  • 时间平移 (Time-shifting)：图像在空间域中的平移（时移）会导致频域中乘以一个复指数因子。该复指数因子只影响相位，不影响幅度。

    $$\mathfrak{J}[f(x-x_0, y-y_0)] = F(u, v)e^{-j2\pi\left(\frac{ux_0}{M} + \frac{vy_0}{N}\right)}$$

  • 频率平移 (Frequency shifting)：空间域中乘以一个复指数因子会导致频率平移。常用于将频域中心 (0, 0) 平移到图像中心 (如 fftshift 操作)。

    $$\mathfrak{J}[f(x, y)e^{-j2\pi\left(\frac{u_0x}{M} + \frac{v_0y}{N}\right)}] = F(u-u_0, v-v_0)\\ \mathfrak{J}[f(x, y)(-1)^{x+y}] = F(u-\frac{M}{2}, v-\frac{N}{2})$$

• 对称性(Symmetry):

  • 平均值 (Average)：
  • 共轭对称性 (Conjugate Symmetric)：
  • 对称性 (Symmetric)：

• 分离性 (Separability): 二维傅里叶变换可以分解为两次一维傅里叶变换(行、列)，这降低了计算复杂度，便于实现快速傅里叶变换（FFT）。

  $$F(u, v) = \frac{1}{N} \sum_{y=0}^{N-1} \left[\frac{1}{M} \sum_{x=0}^{M-1} f(x, y) e^{-j 2\pi \frac{ux}{M}}\right] e^{-j 2\pi \frac{vy}{N}}$$

• 旋转 (Rotation)：图像在空间域中的旋转会导致频域中相应的旋转。如果图像旋转了角度，其频谱也旋转相同角度。

  $$f(r, \theta + \theta_0)\iffF(\omega, \phi + \theta_0)$$

• 周期性 (Periodicity): 离散傅里叶变换具有周期性，频域中的数据在范围内重复。

  $$f(x, y) = f(x + M, y) = f(x, y + N) = f(x + M, y + N)\\ F(u, v) = F(u + M, v) = F(u, v + N) = F(u + M, v + N)$$

• 线性性 (Linearity): 傅里叶变换是线性运算，两个图像的加权组合在频域中仍是对应频域组合的加权和。

  $$\mathfrak{J}[af(x, y) + bg(x, y)] = a\mathfrak{J}[f(x, y)] + b\mathfrak{J}[g(x, y)]$$

• 微分性 (Differentiation): 图像在空间域中的微分对应频域中的乘法运算。二阶微分对应，与拉普拉斯算子相关。

  $$\mathfrak{J}\left[\frac{\partial^n f(x, y)}{\partial x^n}\right] = (j2\pi u)^n \mathfrak{J}[f(x, y)]\\ \mathfrak{J}\left[\nabla^2 f(x, y)\right] = -4\pi^2(u^2 + v^2)F(u, v)$$

• 卷积(Convolution):

• 相关(Correlation):

• 相似性 (Similarity): 图像在空间域中发生缩放时，频域数据会发生相反的缩放，并且幅度会按照缩放比例调整。

  $$\mathfrak{J}[f(ax, by)] = \frac{1}{|ab|} F\left(\frac{u}{a}, \frac{v}{b}\right)$$

4.6.1 总结

名称	表达式
1) 离散傅里叶变换 (DFT) of
2) 逆离散傅里叶变换 (IDFT) of
3) 频谱	$	F(u, v)	= \sqrt{R^2(u, v) + I^2(u, v)}R = \text{Real}(F), I = \text{Imag}(F)$
4) 相位角
5) 极坐标表示	$F(u, v) =	F(u, v)	e^{j\phi(u, v)}$
6) 功率谱	$P(u, v) =	F(u, v)	^2$
7) 平均值
8) 周期性 ( 为整数)
9) 卷积
10) 相关
11) 可分性	2D DFT 可以通过对图像的每一行（或列）计算 1D DFT，再对每一列（或行）计算 1D DFT 得到。详见 Section 4.11。
12) 使用DFT算法计算 IDFT	$MNf^(x, y) = \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F^(u, v)e^{j2\pi\left(\frac{ux}{M} + \frac{vy}{N}\right)}$

---

名称	傅里叶变换对 (DFT Pairs)
1) 对称性质	参见 Table 4.1
2) 线性
3) 平移 (通用)
4) 频域中心移动 (M/2, N/2)
5) 旋转
6) 卷积定理 †
7) 相关定理 †	$\begin{aligned} (f \star h)(x, y) &\iff (F^ \cdot H)(u, v) \ (f^ \cdot h)(x, y) &\iff (1/MN)[(F \star H)(u, v)] \end{aligned}$
8) 离散单位脉冲
9) 矩形
10) 正弦
11) 余弦
12) 微分 (假设边界条件为0)
13) 高斯

注：傅里叶变换对对于连续变量可以进一步推导（以 和 表示空间变量， 和 表示频率变量），这些结果可以通过采样离散变量用于 DFT 工作。

2-D Discrete Fourier Transform

2-D Fourier Transform

定义	说明
傅里叶级数	任何周期性重复的函数都可以表示为不同频率的正弦和/或余弦之和，每个乘以不同的系数。
傅里叶变换	即使不是周期性的函数（但其曲线下面积是有限的）也可以表示为正弦和/或余弦乘以加权函数的积分。
频域	指图像的二维离散傅里叶变换的平面。
傅里叶变换的目的	将信号表示为各种频率的正弦信号的线性组合。

2-D Continuous Fourier Transform

$$j=\sqrt{-1},\quad e^{j\theta}=\cos\theta+j\sin\theta$$

1-D傅里叶变换与逆：

$$F(u)=\int^\infty_{-\infty}f(x)e^{-j2\pi u x}dx\\ f(x)=\int^\infty_{-\infty}F(u)e^{j2\pi u x}du$$

2-D傅里叶变换与逆：

$$F(u,v)=\int^\infty_{-\infty}\int^\infty_{-\infty}f(x,y)e^{-j2\pi (ux+vy)}dxdy\\ f(x,y)=\int^\infty_{-\infty}\int^\infty_{-\infty}F(u,v)e^{j2\pi(ux+vy)}dudv$$

2-D Discrete Fourier Transform

1-D Discrete Fourier Transform

1-D离散傅里叶变换和逆是：

$$F(u)=\frac 1 M\sum^{M-1}_{x=0}f(x)e^{-j\frac{2\pi ux}M}\\ f(x)=\sum^{M-1}_{u=0}F(u)e^{j\frac{2\pi ux}M}$$

因为,离散傅里叶变换可以被写成：

$$F(u)=\frac 1 M\sum^{M-1}_{x=0}f(x)\left[\cos\frac{2\pi ux}M-j\sin\frac{2\pi ux}M\right]$$

• 频率（时间）域：的值所在的域（ 的值）；因为决定了变换分量的频率。
• 频率（时间）分量：的个项中的每一个。

极坐标表示（谱=函数）

$$F(u)=\vert F(u)\vert e^{j\phi(u)}$$

• : 幅度谱，用于描述频率成分的强度。
• ：相位谱，用于描述频率成分的相位信息。
• 是频域函数的实部，是频域函数的虚部。

功率谱：, 用于量化图像在不同频率处的能量分布，是幅度谱的平方。

2-D Discrete Fourier Transform

$$F(u,v)=\frac{1}{MN}\sum^{M-1}_{x=0}\sum^{N-1}_{y=0}f(x,y)e^{-j2\pi\left(\frac{ux}M+\frac{vy}N\right)}\\ f(x,y)=\sum^{M-1}_{x=0}\sum^{N-1}_{y=0}F(u,v)e^{j2\pi\left(\frac{ux}M+\frac{vy}N\right)}$$

• : 幅度谱
• : 相位谱
• : 功率谱

二维离散傅里叶变换的性质(Properties of 2-D DFT)

1. 平移(shifting)：

   • 时间平移 (Time-shifting)：图像在空间域中的平移（时移）导致幅度谱不变、相位谱变化。

     $$\begin{align} \mathfrak{J}[f(x-x_0, y-y_0)]&= F(u, v)e^{-j2\pi\left(\frac{ux_0}{M} + \frac{vy_0}{N}\right)}\\ f(x-x_0,y-y_0)&=\sum^{M-1}_{x=0}\sum^{N-1}_{y=0}F(u,v)e^{j2\pi\left(\frac{ux-ux_0}M+\frac{vy-vy_0}N\right)}\\&=\sum^{M-1}_{x=0}\sum^{N-1}_{y=0}F(u,v)e^{j2\pi\left(\frac{ux}M+\frac{vy}N\right)}e^{-j2\pi\left(\frac{ux_0}{M} + \frac{vy_0}{N}\right)}\\ \mathfrak{J}[f(x-x_0, y-y_0)]&= F(u, v)e^{-j2\pi\left(\frac{ux_0}{M} + \frac{vy_0}{N}\right)} \end{align}$$

   • 频率平移 (Frequency shifting)：空间域中乘以一个复指数因子会导致频率平移。式2常用于将频域中心 (0, 0) 平移到图像中心 (如 fftshift 操作)。

     $$\mathfrak{J}[f(x, y)e^{j2\pi\left(\frac{u_0x}{M} + \frac{v_0y}{N}\right)}] = F(u-u_0, v-v_0)\\ \mathfrak{J}[f(x, y)(-1)^{x+y}] = F(u-\frac{M}{2}, v-\frac{N}{2})\\ proof.\ u_0=\frac M 2,v_0=\frac N2\\ \mathfrak{J}[f(x, y)e^{j2\pi\left(\frac{u_0x}{M} + \frac{v_0y}{N}\right)}] =\mathfrak{J}[f(x, y)e^{j\pi(x+y)}]=\cos {\pi(x+y)}+j\sin {\pi(x+y)}=(-1)^{x+y}\\$$

2. 对称性(Symmetry):

   • 平均值 (Average)： 是直流量，相当于中心点=平均值。
   • 共轭对称性 (Conjugate Symmetric)：
   • 对称性 (Symmetric)：

3. 分离性 (Separability): 二维傅里叶变换可以分解为两次一维傅里叶变换(行、列)，这降低了计算复杂度，便于实现快速傅里叶变换（FFT）。

   $$F(u, v) = \frac{1}{N} \sum_{y=0}^{N-1} \left[\frac{1}{M} \sum_{x=0}^{M-1} f(x, y) e^{-j 2\pi \frac{ux}{M}}\right] e^{-j 2\pi \frac{vy}{N}}$$

4. 旋转 (Rotation)：图像在空间域中的旋转会导致频域中相应的旋转。如果图像旋转了角度，其频谱也旋转相同角度。

   $$f(r, \theta + \theta_0)\iff F(\omega, \phi + \theta_0)$$

5. 周期性 (Periodicity): 离散傅里叶变换具有周期性，频域中的数据在范围内重复。

   $$f(x, y) = f(x + M, y) = f(x, y + N) = f(x + M, y + N)\\ F(u, v) = F(u + M, v) = F(u, v + N) = F(u + M, v + N)$$

6. 线性性 (Linearity): 傅里叶变换是线性运算，两个图像的加权组合在频域中仍是对应频域组合的加权和。

   $$\mathfrak{J}[af(x, y) + bg(x, y)] = a\mathfrak{J}[f(x, y)] + b\mathfrak{J}[g(x, y)]$$

7. 微分性 (Differentiation): 图像在空间域中的微分对应频域中的乘法运算。二阶微分对应，与拉普拉斯算子相关。

   $$\mathfrak{J}\left[\frac{\partial^n f(x, y)}{\partial x^n}\right] = (j2\pi u)^n\mathfrak{J}[f(x, y)]= (j2\pi u)^n F(u,v)\\ \mathfrak{J}\left[\nabla^2 f(x, y)\right] = -4\pi^2(u^2 + v^2)F(u, v)$$

8. 卷积(Convolution):

9. 相关(Correlation):

10. 相似性 (Similarity): 图像在空间域中发生缩放时，频域数据会发生相反的缩放，并且幅度会按照缩放比例调整。

    $$\mathfrak{J}[f(ax, by)] = \frac{1}{|ab|} F\left(\frac{u}{a}, \frac{v}{b}\right)$$

一些常用的傅里叶变换对 (FT Pairs)

1. 单位冲激函数()：

   函数与其他函数卷积，就等于这个函数本身。

   $$\delta(x)*g(x)\iff F(\delta(x))G(x)\\ g(x)\iff 1\times G(x)$$

2. 高斯函数: 空间域是高斯函数，频率域仍是高斯函数，但与空间域的标准差成反比。

   $$A2\pi\sigma^2 \exp(-2\pi^2\sigma^2(x^2 + y^2))\iff A \exp\left(-\frac{u^2 + v^2}{2\sigma^2}\right)$$

   高斯函数的FT仍是高斯函数，中心在频率。

   $$\exp(-\pi(x^2 + y^2))\iff\exp(-\pi(u^2 + v^2))$$

3. 正弦函数: 空间域是正弦函数，频率域则是两个对称的冲激函数，分别位于, 但幅度带有和相反的符号。

   $$\sin(2\pi u_0x + 2\pi v_0y)\iff\frac{1}{2} j \left[ \delta(u+u_0, v+v_0) - \delta(u-u_0, v-v_0) \right]$$

4. 余弦函数: 空间域是余弦函数，频率域则是两个对称的冲激函数，分别位于.

   $$\cos(2\pi u_0x + 2\pi v_0y)\iff\frac{1}{2} \left[ \delta(u+u_0, v+v_0) + \delta(u-u_0, v-v_0) \right]$$

空间域中的正弦信号也在频域中产生两个对称的冲激，但其相位不同于余弦。

Filtering in the Frequency Domain

卷积定理：$f(x, y) h(x, y)F(u, v) H(u, v)$组成傅里叶变换对。左边的表达式(空间域卷积)可以通过对右边表达式进行傅里叶反变换获得；右边的表达式可以通过对左式进行正向傅里叶变换获得。*频率域的卷积被简化为空间域的乘法，反之亦然。

$$\mathfrak{J}[f(x, y) * h(x, y)]= F(u, v) H(u, v)\\ \mathfrak{J}[f(x, y)h(x, y)] =F(u, v)* H(u, v)$$

相关定理：

$$\mathfrak{J}[f(x, y) \star h(x, y)]= F^*(u, v) H(u, v)\\ \mathfrak{J}[f^*(x, y)h(x, y)] =F(u, v)\star H(u, v)\\\\ \mathfrak{J}[f(x, y) \star f(x, y)]=\vert F(u, v) \vert^2\\ \mathfrak{J}[\vert f(x, y)\vert^2] =F(u, v)\star F(u, v)$$

伸缩性质：

$$\mathfrak{J}[f(ax, by)]= \frac{1}{\vert ab\vert}F(\frac u a, \frac v b)$$

【能量保持 · 帕斯瓦尔定理】如果离散的信号是一维的，对每个信号平方求和，再进行傅里叶变换，频域上也能得到一致的平方和。信号再时域和频域之间能量不变。

频域滤波

基本思想 ：通过选择一个特定的滤波器传递函数来修改图像的傅里叶变换。

基于卷积定理的频域滤波实现：

1. 通过傅里叶变换将图像从空间域转换到频域。
2. 在频域中对傅里叶变换结果乘以滤波器。
3. 通过傅里叶逆变换将结果转换回空间域，得到滤波后的图像。

Wraparound Error（混叠误差）: 在频域卷积时，完整信号可以被切分成多个简单信号相加。那么这些简单信号在交叠处：究竟是取信号1的值、还是取信号2的值呢？

解决方法： 对图像进行零填充 (Padding)，扩展信号范围，避免非零部分的干扰。就是改变简单信号的周期，让其周期=完整信号的周期，然后会有一些部分，然后全部=0（这个就叫零填充）。

从空域滤波器中获取频域滤波器(Obtaining Frequency Domain Filters from Spatial Filters)

Q: Why?

A: 1.效率 2.有意义的比较

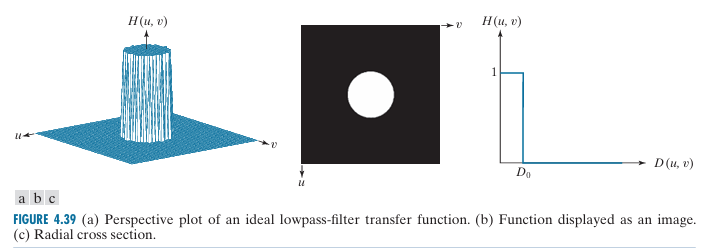
理想低通滤波器(ILPF)：

$$H(u,v)=\begin{cases} 1, \quad D(u,v)\le D_0\\ 0,\quad D(u,v)> D_0\\ \end{cases}$$

其中是从点到频率矩阵中心的距离:

$$D(u,v)=\sqrt{\left(u-\frac M 2\right)^2+\left(v-\frac N 2\right)^2}$$

巴斯沃斯低通滤波器(Butterworth Lowpass Filters, BLPFs):

$$H(u,v)=\frac{1}{1+\left[\frac{D(u,v)}{D_0}\right]^{2n}}$$

随n增大，会越来越趋近于理想的低通滤波器。当，因此永远过0.5的点。

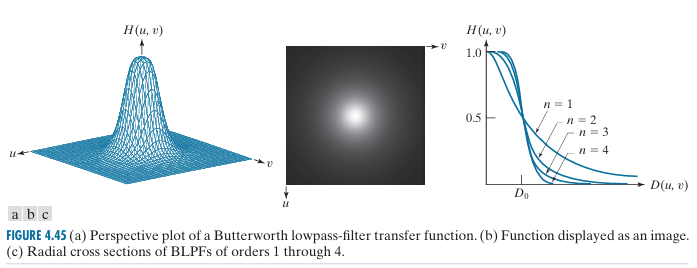
高斯低通滤波器( Gaussian Lowpass Filters, GLPFs)

$$H(u,v)=\exp\{\frac{-D^2(u,v)}{2D^2_0}\}$$

频率锐化滤波器(Sharpening Frequency Domain Filters)

通用高通频域滤波器：

$$H_{hp}(u,v)=1-H_{lp}(u,v)$$

高通滤波器	公式
理想高通滤波器
巴斯沃斯高通滤波器
高斯高通滤波器