Ch9 聚类分析

[TOC]

聚类分析的基本思想: 将样本(or 变量) 按相似程度的大小聚在一起，逐一分类。

相似程度的度量：距离或相似系数代表样本或变量之间的相似程度。

样本之间定义距离
变量之间定义相似系数

9.1 个体聚类&变量聚类

假设有个个体，每个个体有个观测变量(指标)。ps:所以对齐不同的细粒度。

个体聚类	变量聚类
根据个体与个体间观测值的差别和相似之处，将这个个体分成若干个类别。	根据变量与变量之间的差别和相似之处，将这个变量分成若干个类别。
栗子：欧洲各国语言的语系分类。	栗子：人体部位尺寸的分类。

9.2 距离、相似系数和匹配系数

9.2.1 个体聚类

个体之间的接近程度通常用Minkowski距离来度量。设，，则与的Minkowski距离为 $其中$

$d(x,y)=\begin{cases} \sum_{i = 1}^{p}\vert x_i - y_i\vert, & m = 1\\ \left(\sum_{i = 1}^{p}(x_i - y_i)^2\right)^{1/2}, & m = 2\\ \max_{1\leq i\leq p}\vert x_i - y_i\vert, & m=\infty \end{cases}$

分别为绝对距离、欧氏距离、Chebyshev距离。 注1. 具体问题可用合适的距离，特别是离散型数据。

9.2.2 变量聚类

Pearson矩相关系数

# 变量之间的接近程度通常用Pearson矩相关系数来度量设变量和在个个体的观测值分别为和，则变量和之间的距离（相似系数）为

$d(w, u) = r_{w, u} = \frac{\sum_{i = 1}^{n} (w_i - \bar{w})(u_i - \bar{u})}{\sqrt{\sum_{i = 1}^{n} (w_i - \bar{w})^2} \sqrt{\sum_{i = 1}^{n} (u_i - \bar{u})^2}}$

其中，，。 注2. 时，。

夹角余弦

变量之间的接近程度的另一个常用度量是夹角余弦，定义如下：设两个变量分别为和，则变量和之间的夹角余弦为

$d(x,y)=\frac{\sum_{i = 1}^{n}x_iy_i}{\sqrt{\sum_{i = 1}^{n}x_i^2}\sqrt{\sum_{i = 1}^{n}y_i^2}}$

此度量常用于处理图形的相似性。

9.2.3 匹配系数

假设有两个观测向量，则与的匹配系数为:

$d(x,y)=\frac{\sum_{i = 1}^{k}I(x_i = y_i)}{k}$

匹配系数常用于属性数据的相似性度量。

9.3 聚类方法

聚类方法大致分为：谱系聚类、迭代分块聚类

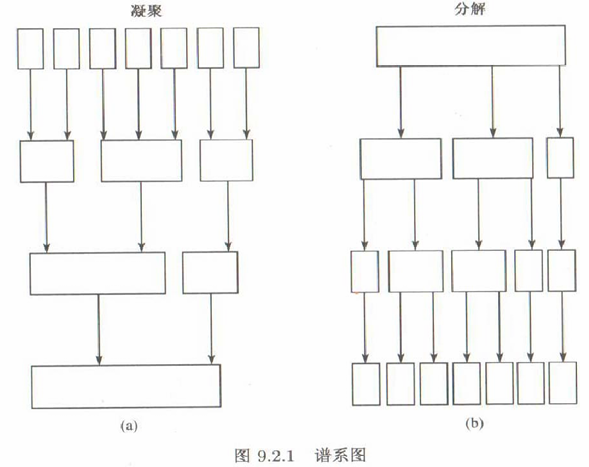
谱系聚类（比较基本传统）分为以下两种类型（关键: 类与类之间的度量）：

	凝聚	分解
简介	类别由多到少.	类别由少到多.
方法	一开始把每个个体(变量)自成一类,然后将最接近的个体(最相似的变量)凝聚为一小类，再将最接近相似)的类凝聚在一起,依次类推直到所有个体(变量)凝聚为一个大类时止.	一开始把所有个体(变量)看成一大类,然后将它分解成两个子类,使这两个子类最为疏远,再将子类分为两个最为疏远的子类,依此类推直到每个个体(变量)都自成一类时止.
缺陷	一旦两个个体(变量)被分入同一个类中,则它们以后不再会分入两个不同的类中.	一旦两个个体(变量)被分入两个不同的类中,则它们以后不再会并入同一个类中.
缺陷（相同）	个体被错误分类无法纠正	个体被错误分类无法纠正
缺陷（相同）	计算量大	计算量大

9.3.2 类之间距离

设有两个由个体或变量组成的类类与之间的距离常用以下定义方法：

方法	公式
(1). 最小距离法
(2). 最大距离法
(3). 类平均法	, 其中， $You can't use 'macro parameter character #' in math moden_1 = # \{x_i : i \in G_1\}$ ， $You can't use 'macro parameter character #' in math moden_2 = # \{x_j : j \in G_2\}$ 。
(4). 重心法	，其中，，.
(5). 离差平方和法

注3：离差平方和即组间平方和，事实上有 :
$\begin{align} d(\pi_1, \pi_2)&=\frac{n_1n_2}{n_1 + n_2}(\bar{x}_1-\bar{x}_2)'(\bar{x}_1-\bar{x}_2) \\ &=n_1(\bar{x}_1-\bar{x})'(\bar{x}_1-\bar{x})+n_2(\bar{x}_2-\bar{x})'(\bar{x}_2-\bar{x})\\ 其中\bar{x}&=\frac{1}{n_1 + n_2}\left(\sum_{i\in G_1}x_i+\sum_{j\in G_2}x_j\right) \end{align}$

如果只有两类的话，分解法不靠谱。存在的问题就是：错误是积累的，连锁反应。

9.3.3 对谱系分解的改进：迭代分块聚类

迭代分块聚类法是一种动态聚类法,其搜索迭代步骤大致如下:

—-	迭代分块聚类法
1. 初始分类	将n个个体(变量)初始分为k类,其中,类的个数k可以事先给定(K-means),也可以在聚类过程中逐步确定(动态K-means)。
2. 修改分类	对每个个体(变量)逐一进行搜索,若将某个个体变量)分入另一个类后对分类有所改进,则将其移入改进最多的那个类,否则其不移动，仍在原来的类中。
3. 重复迭代	在对每个个体(变量)逐一都进行搜索之后,重复第(2)步，直到任何一个个体(变量)都不需要移动为止，从而得到最终分类。

K-means

由于初始分类数k事先给定,且迭代过程中不断计算类的重心，故称该聚类方法为k均值法(k-means)：

—-	K-means
1. 初始分类	将几个个体初始分成k类,k事先给定.
2. 修改分类	计算初始k类的重心。然后对每个个体逐一计算它到初始k类的距离(通常用该个体到类的重心的欧氏距离)。若该个体到其原来的类的距离最近,则它保持类不变，否则它移入离其距离最近的类，重新计算由此变动的两个类的重心。
3. 重复迭代	在对所有个体都逐一进行验证,是否需要修改分类之后，重复步骤2),直到没有个体需要移动为止,从而得到最终分类.

动态K-means

事先给定3个数: 类别数k,阀值和 , .

相较于K-means, 动态K-means在聚类过程中动态地调整聚类中心的数量 K。通常根据数据的分布和内部结构来自动确定合适的 K 值，避免了手动选择 K 值带来的不确定性。

—-	动态K-means
1. 选取聚点	取前k个个体作为初始聚点,计算这k个聚点两两之间的距离若最小的距离比小,则将最小距离的这两个聚点合并在一起,并用它们的重心作为新的聚点，重复上述过程,直到所有的聚点两两之间的距离都不比小时为止,因此，此时聚点的个数可能小于k.
2. 初始分类	对余下的n-k个个体逐一进行计算，对输入的一个个体，分别计算它到所有聚点的距离。若该个体到所有聚点的距离都大于，则它作为一个新的聚点，这时所有聚点两两之间的距离都不比小，否则将它归入离它最近的那一类，并重新计算接受该个体的那个类的重心以代替该类原来的聚点。然后重复步骤1)，再次验证所有聚点两两之间的距离是否都不比小，如果比小就将其合并，直到所有聚点两两之间的距离都不比小时止，该步完成后，聚点的个数可能小于k，也可能大于k。
3. 重复迭代	在对所有个体都逐一进行验证，是否需要修改分类之后，重复步骤2)，直到没有个体需要移动为止，从而得到最终分类。这时，最终个体的类别数不一定是 k。

例子

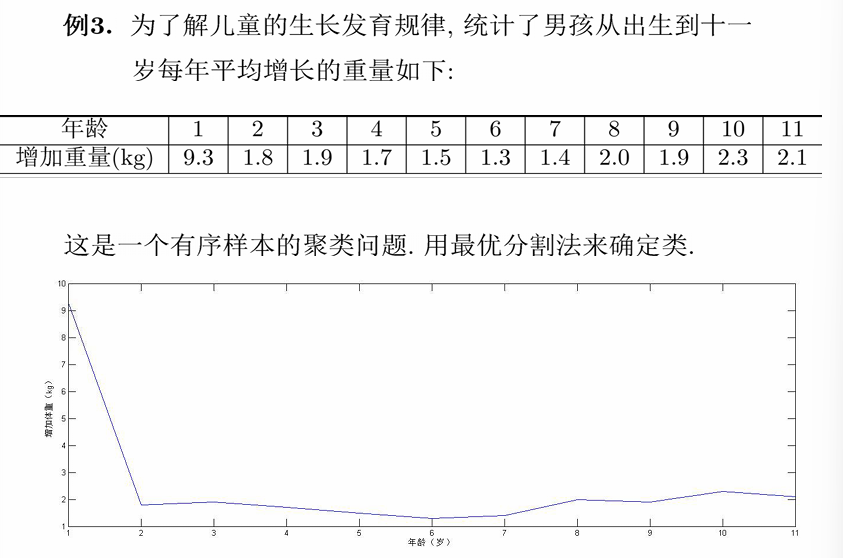
计算直径:

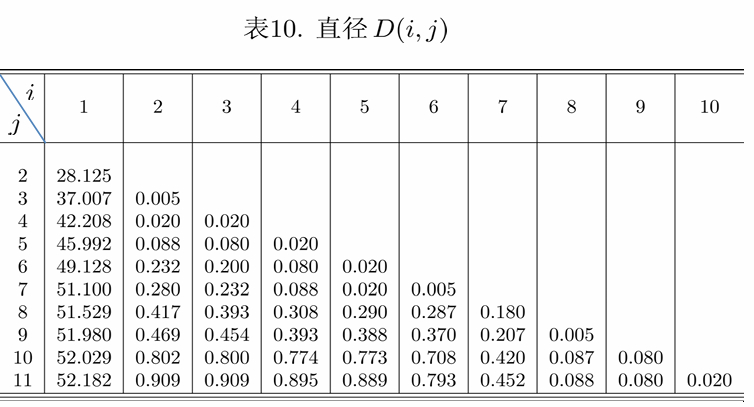
计算最小目标函数：

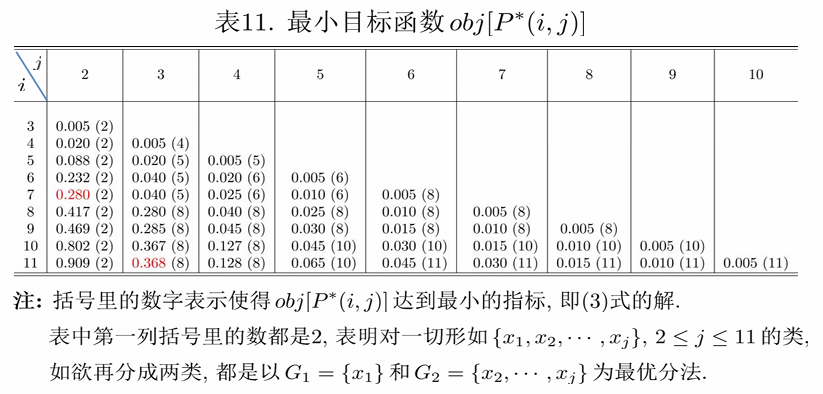
最终的3类划分：

确定k：从图上的曲线变化率，分成3类或4类最为合适。

多元统计分析-Ch9-聚类分析