Ch8 判别分析

[TOC]

8.0 引入

对观测到的样本判断它属于哪个总体(类)。实际上就干一件事：分类样本。

判别分析的数学描述：已知有k个总体(类), 题目对应的分布函数分别是(属于m维的函数)。给定一个样本y，判断y来自哪个总体(类)。

8.1 距离判别

假设有两个正态总体，分布分别为. 判断样本y来自哪个总体。

扩展欧式距离—>马氏距离(Mahalanobis距离)

设和是来自于均值为，协方差阵为的总体的两个样本，定义样本之间的马氏距离为:
$d^2(x,y)=(x - y)'\Sigma^{-1}(x - y).$
定义与总体的距离为与均值的距离，即:
$d^2(x,G)=(x - \mu)'\Sigma^{-1}(x - \mu).$

8.1.1 总体具有相同协方差的情形

假定两个总体具有相同的协方差阵.

我们先考虑总体和分别服从正态分布和的距离判别方法，然后给出一般总体的判别方法。

思路：利用样本到总体的马氏距离进行判断。
$d^2(y, G_1)=(y - \mu_1)'V^{-1}(y - \mu_1)\\ d^2(y, G_2)=(y - \mu_2)'V^{-1}(y - \mu_2)$

样本到总体的距离差为:

$d^2(y, G_1)-d^2(y, G_2)=-2\left(y - \frac{\mu_1 + \mu_2}{2}\right)'V^{-1}(\mu_1 - \mu_2)$

记:

$\bar{\mu}=\frac{\mu_1 + \mu_2}{2}\\ W(y)=(y - \bar{\mu})'V^{-1}(\mu_1 - \mu_2)$

有:

$d^2(y, G_1)-d^2(y, G_2)=-2W(y)$

判别准则为:

$\begin{cases}y \in G_1, & \text{若} W(y) \geq 0; \\ y \in G_2, & \text{若} W(y) < 0.\end{cases}$

若记，则是的线性函数。

则称是线性判别函数，称是判别系数。

注：上述结果可以推广到非正态分布的情形，只需知道均值和协方差。

A.总体参数未知的情形

当，和未知时，需要训练样本来估计总体的这些参数。

假设已知有总体的个样本，，，和总体的个样本，，。令:

$\bar{y}^{(1)}=\frac{1}{n_1}\sum_{i = 1}^{n_1}y_i^{(1)},\quad \bar{y}^{(2)}=\frac{1}{n_2}\sum_{i = 1}^{n_2}y_i^{(2)}\\ \begin{align} \hat{V}&=\frac{1}{n_1 + n_2 - 2}\left[\sum_{i = 1}^{n_1}(y_i^{(1)}-\bar{y}^{(1)})(y_i^{(1)}-\bar{y}^{(1)})'+\sum_{i = 1}^{n_2}(y_i^{(2)}-\bar{y}^{(2)})(y_i^{(2)}-\bar{y}^{(2)})'\right]\\ &\overset{\Delta}=\frac{1}{n_1 + n_2 - 2}[S_1 + S_2] \end{align}$

需要注意的是表示离差阵、而表示协方差阵。此时的判别函数为：

$W(y)=\left( y - \frac{\bar{y}^{(1)} + \bar{y}^{(2)}}{2} \right)'\hat{V}^{-1} (\bar{y}^{(1)} - \bar{y}^{(2)})$

判别准则同上：

$\begin{cases} y\in G_1, 若W(y)\ge0\\ y \in G_2,若W(y)< 0 \end{cases}$

B.多个总体的判别问题

定义：令是空间的子集，若它们满足:

$D_i \cap D_j = \varnothing,\ i \neq j,\ 1 \leq i < j \leq k\\ \bigcup_{i = 1}^{k} D_i = R^m$

称为的一个划分。

(1) 总体参数已知的情形

设有个总体，它们的均值和协方差阵分别是和。这时的(两两)判别函数为:

$W_{ij}(y) = (y - \frac{\mu_i + \mu_j}{2})'V^{-1}(\mu_i - \mu_j),1 \leq i \neq j \leq k$

判别规则为:

$y属于总体G_{i}，\text{if}\ y\in D_{i},\ 1\leq i\leq k$

其中:

$D_{i}=\{y\in R^{m}:W_{ij}(y)>0,\ 对所有j\neq i成立\},\ 1\leq i\leq k$

若，则判定属于总体，或属于，，或属于，即边界上的点可以判定它属于任意相邻区域所代表的总体。

(2)总体参数未知的情形

假设有来自总体的样本，。

记。令:

$\bar{y}^{(i)}=\frac{1}{n_i}\sum_{j = 1}^{n_i}y_j^{(i)},\ 1\leq i\leq k\\ \hat{V}=\frac{1}{n - k}\sum_{i = 1}^{k}S_i$

则判别函数为:

$W_{ij}(y)=\left(y-\frac{\bar{y}^{(i)}+\bar{y}^{(j)}}{2}\right)'\hat{V}^{-1}(\bar{y}^{(i)}-\bar{y}^{(j)}),\ 1\leq i\neq j\leq k$

判别规则仍为:

$\begin{cases} y\in G_1, 若W(y)\ge0\\ y \in G_2,若W(y)< 0 \end{cases}$

8.1.2 总体协方差不同

假设有个总体，它们的均值和协差阵分别是。

总体参数已知

令：

$D_i=\left\{y\in R^m:d^2(y,G_i)\leq\min_{1\leq j\leq k,j\neq i}d^2(y,G_j)\right\},\ 1\leq i\leq k$

则判别规则为:

$y属于总体G_i\ \text{if}y\in D_i,\ 1\leq i\leq k$

总体参数未知

使用样本均值和样本协方差阵来估计样本，需要注意的是表示离差阵、而表示协方差阵。记:

$\bar{y}^{(i)}=\frac{1}{n_i}\sum_{j = 1}^{n_i}y_j^{(i)},\ 1\leq i\leq k\\ \hat{V}_i=\frac{S_i}{n_i - 1},\ 1\leq i\leq k$

令:

$\hat{d}^2(y,G_i)=(y - \bar{y}^{(i)})'\hat{V}_i^{-1}(y - \bar{y}^{(i)}),\ 1\leq i\leq k$

则判别规则同总体参数已知。

8.2 贝叶斯判别

对样本来自哪个总体的可能性有一定的认识，才使用贝叶斯判别。

问题描述：设有个总体，它们的维密度函数分别为。记是的一个划分。

判别规则为：

$y属于总体G_i,\text{if}y\in D_i,\ 1\leq i\leq k$

8.2.1 贝叶斯判别法则

记为样本来自总体，但被误判属于总体的损失，。
假定样本来自总体的先验概率为，，。
这等价于，的密度函数为：

$y\stackrel{d}{\sim}p(y)=\sum_{i = 1}^{k}\pi_ip_i(y)$

贝叶斯判别法则	求解最优划分，使得误判的平均损失最小。
误判概率(同时发生将其判别为j&误判i)	给定划分，样本来自总体，但被误判属于总体的概率为 :
判别的平均损失	给定划分，相应判别的平均损失为

贝叶斯判别法则就是选择划分，使得判别的平均损失最小。

注1：假定划分不包含边界。因此边界。

假定：若样本，则，即边界的测度为0。

Q: 测度为0？

A: 边界的测度为0表示边界是“低维流形”，在高维空间中，它的体积（或者概率质量）可以忽略不计。概率论上，如果一个集合的测度为0，则样本落在该集合上的概率为零。

在一维空间，边界是点（0维），其测度为0。

在二维空间，边界是曲线（1维），其面积为0。

在三维空间，边界是曲面（2维），其体积为0。

边界测度为0的含义: 贝叶斯判别中，区域边界是由等式定义的，其中是将样本 y 判为类别的贝叶斯风险。边界的测度为0意味着：. 这表示：

从概率的角度，样本几乎不可能恰好落在边界上。

但这并不严格保证“没有样本落在边界上”，因为对于有限样本，可能存在样本 y 落在边界上。

Q: 为什么边界测度为0很重要？

A: 边界测度为0的性质使得贝叶斯判别区域的定义是严格划分的，区域之间互不重叠，且几乎覆盖整个样本空间; 确保贝叶斯判别的理论正确性。

由于边界的概率质量为零，样本落在边界上的概率可以忽略不计。

因此，贝叶斯判别规则在实际应用中是稳定的，不会因为边界问题产生重大影响。

8.2.2 样本空间中不同类别之间的判别边界测度为0

积分区域不同，只有两者相交的地方才是0（？）

定理8.1：当先验概率，总体的密度函数以及损失函数都给定时，贝叶斯判别的解为 :

$D_i=\{y:h_i(y)<h_j(y),1\leq j\leq k,j\neq i\},\ 1\leq i\leq k\\ h_i(y)=\sum_{\substack{j = 1\\j\neq i}}^k\pi_jp_j(y)L(j,i),1\leq i\leq k$

贝叶斯划分边界的测度为0:

$\sum_{i = 1}^k\sum_{\substack{j = 1\\j\neq i}}^k\int_{\{h_i(y)=h_j(y)\}}p(x)dx = 0$

证明: 若令，则平均损失为:
$\begin{align}g(D_1,\cdots,D_k)&=\sum_{i = 1}^k\pi_i\sum_{\substack{j = 1\\j\neq i}}^kL(i,j)P(j|i;D_1,\cdots,D_k)\\ &=\sum_{i = 1}^k\pi_i\sum_{j = 1}^kL(i,j)P(j|i;D_1,\cdots,D_k)\\ &=\sum_{i = 1}^k\sum_{j = 1}^k\pi_iL(i,j)\int_{D_j}p_i(y)dy\\ &=\sum_{j = 1}^k\int_{D_j}h_j(y)dy \end{align}$
若空间存在另一个划分，其平均损失为:
$g(D_1^*,\cdots,D_k^*)=\sum_{i = 1}^k\int_{D_i^*}h_i(y)dy$
则：
$\begin{align*} &g(D_1,\cdots,D_k)-g(D_1^*,\cdots,D_k^*)\\ =&\sum_{i = 1}^{k}\sum_{j = 1}^{k}\int_{D_i\cap D_j^*}(h_{ij}(y)-h_{ji}(y))p(x)dy \end{align*}$
而由的定义，知在上对一切成立，故:
$g(D_1,\cdots,D_k)-g(D_1^*,\cdots,D_k^*)\leq0\\ g(D_1,\cdots,D_k)\leq g(D_1^*,\cdots,D_k^*)$
说明使得平均损失达到极小，它就是贝叶斯判别的解。再由知，对任意成立。而边界由集合交并运算构成，因此是测度意义下的零测集。

注2：表示判定样本属于总体的平均损失。定理表明使总平均损失最小与使每个最小是等价的。注3：若取，则贝叶斯解为

$D_i = \{y\in R^m:\pi_ip_i(y)>\pi_jp_j(y),j\neq i,1\leq j\leq k\}.\quad(13)$

事实上，对任意，有

$h_{ii}(y)=\sum_{\substack{j = 1\\j\neq i}}^{k}\pi_jp_j(y)L(i,j)=\sum_{\substack{j = 1\\j\neq i}}^{k}\pi_jp_j(y)-\pi_ip_i(y)$

由定理8.1得贝叶斯解。

8.2.3 贝叶斯判别的容许性

Q: 容许估计？

A: 对于一个估计量，如果存在另一估计量，使得，，且至少对一个严格不等，则称为不可容许的。如果不存在上述性质的，则称为可容许的。要求估计必须是可容许的，就是在要求“风险一致最小”，在大多数情况下可容许的估计是有偏的。

定理8.3 (容许性) 若，，则贝叶斯解是容许的。证明：设为贝叶斯解，如果它不是容许的，则存在另一个划分$D^ $，使得$ L(i;D_1^,\cdots,D_k^) \leq L(i;D_1,\cdots,D_k), \quad 1\leq i\leq k, $且存在某个$ i_0 $使得$ L(i_0;D_1^,\cdots,D_k^*) < L(i_0;D_1,\cdots,D_k), $ 因此有

$\begin{align*} g(D_1^*,\cdots,D_k^*) &= \sum_{i = 1}^{k} \pi_i L(i;D_1^*,\cdots,D_k^*) \\ &< \sum_{i = 1}^{k} \pi_i L(i;D_1,\cdots,D_k) \\ &= g(D_1,\cdots,D_k). \end{align*}$

这与是贝叶斯解矛盾！故是容许的。

例子(什么，是栗子，吃一口)

例8.4 设两个总体和分别为和，，。此时

$p_1(y)=(2\pi)^{-m/2}|V|^{-1/2}\exp\left\{-\frac{1}{2}(y - \mu_1)'V^{-1}(y - \mu_1)\right\}\\ p_2(y)=(2\pi)^{-m/2}|V|^{-1/2}\exp\left\{-\frac{1}{2}(y - \mu_2)'V^{-1}(y - \mu_2)\right\}.$

由(10)知若，则

$D_1=\{y:\pi_2p_2(y)L(2,1)<\pi_1p_1(y)L(1,2)\}\\ D_2=\{y:\pi_2p_2(y)L(2,1)>\pi_1p_1(y)L(1,2)\}$ $\begin{align} c&\overset{\Delta}{=}\frac{\pi_2L(2,1)}{\pi_1L(1,2)}<\frac{p_1(y)}{p_2(y)}\\ &<\exp\left\{\frac{1}{2}(y - \mu_1)'V^{-1}(y - \mu_1)-\frac{1}{2}(y - \mu_2)'V^{-1}(y - \mu_2)\right\} \end{align}$

取对数回到前面的距离判别。

化简后不难推得

$\left(y - \frac{\mu_1 + \mu_2}{2}\right)'V^{-1}(\mu_1 - \mu_2) > \log c.$

由(1)式即知

$D_1 = \{y: W(y) > \log c\}\\ D_2 = \{y: W(y) < \log c\}$

当，时，，。即当两总体先验概率相等，误判损失为常数时，贝叶斯判别与距离判别等价。

真正的贝叶斯是基于后验概率，进行判别：

注4：基于后验概率的判别当样本已知时，它来自总体的条件（后验）概率为则判别准则为 $属于总体，若，$

因为密度估计本身存在困难，所以贝叶斯估计只是理论上成立的。

8.3 Fisher 判别

总体协方差阵相同、距离判别+正态总体下贝叶斯判别—>线性判别函数。

当总体的协方差阵相同时，距离判别以及正态总体下的贝叶斯判别都导出一个线性判别函数。

8.3.1 线性判别函数

设维总体的均值和协方差阵分别为和，。给定向量，任给样本，考虑它的线性函数，有

$u_i = E(\alpha(y)|G_i)=\alpha'\mu_i, \quad 1\leq i\leq k\\ v_i^2 = V_{ar}(\alpha(y)|G_i)=\alpha'V_i\alpha, \quad 1\leq i\leq k$

令：

$B_0 = \sum_{i = 1}^{k} \left(u_i - \frac{1}{k} \sum_{j = 1}^{k} u_j\right)^2\\ E_0 = \sum_{i = 1}^{k} v_i^2 = \sum_{i = 1}^{k} \alpha'V_i\alpha$

可以看做是方差分析里的组间差，是组内差。

Fisher准则：选取使得

$\alpha^* = \underset{\alpha \neq 0}{\arg\max_{\alpha \in R^m}} \Delta(\alpha) = \underset{\alpha \neq 0}{\arg\max_{\alpha \in R^m}} \frac{B_0}{E_0}$

称为判别效率。

记，，。易知：

$\Delta(\alpha) = \frac{B_0}{E_0} = \frac{\alpha'B\alpha}{\alpha'E\alpha}$

定理8.5 ：假设，则Fisher准则下的线性判别函数的解为的最大特征根所对应的正则特征向量，且相应的判别效率为。

证明：利用二次型的极值性质得。

注5：当，时，Fisher准则下的线性判别函数和判别效率为
$\alpha^{*}(y)=y'(V_1 + V_2)^{-1}(\mu_1 - \mu_2)\\ \Delta(\alpha^{*})=\frac{1}{2}(\mu_1 - \mu_2)'(V_1 + V_2)^{-1}(\mu_1 - \mu_2).$
事实上，此时，。不难推知是的特征向量，其对应非零特征根是：
$\lambda^{*}=\Delta(\alpha^{**})=\frac{1}{2}(\mu_1 - \mu_2)'(V_1 + V_2)^{-1}(\mu_1 - \mu_2)$

总体参数未知的情形

基于训练样本可以估计总体的均值和协方差阵，进而得到线性判别函数为

$\alpha(y) = y'(S_1 + S_2)^{-1}(\bar{y}_1 - \bar{y}_2)$

注6: Fisher准则的判别函数不唯一。

事实上，假设（不一定线性）是Fisher准则的判别函数，对任意和，令，有:

$\frac{B_0^*}{E_0^*} = \frac{B_0}{E_0} \Rightarrow \Delta(\alpha^*(y)) = \Delta(\alpha(y))$

即也是Fisher准则的判别函数。

8.3.2 Fisher判别准则

对于线性判别函数，当时，令 Fisher判别准则的划分为

$D_1=\{y:\alpha'(y - \bar{\mu})\geq0\}\\ D_2=\{y:\alpha'(y - \bar{\mu})<0\}$

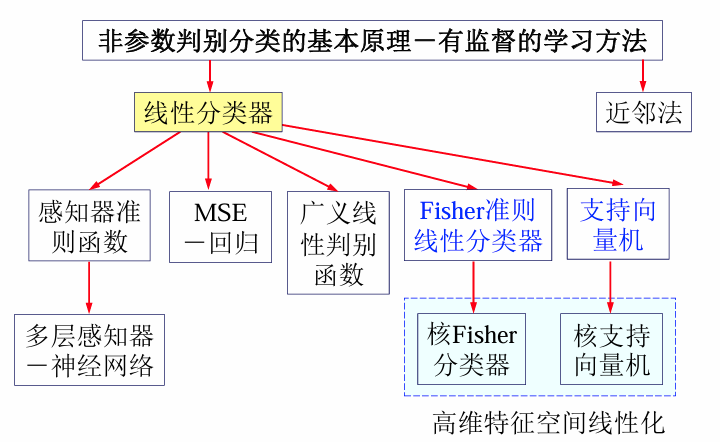
8.4 判别分析实例

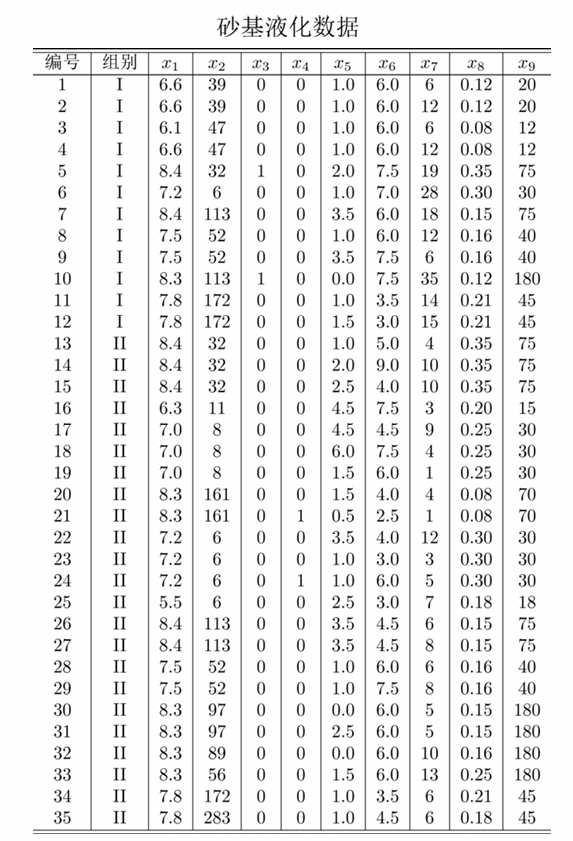
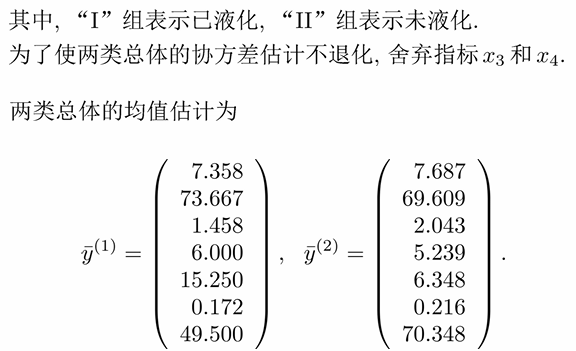
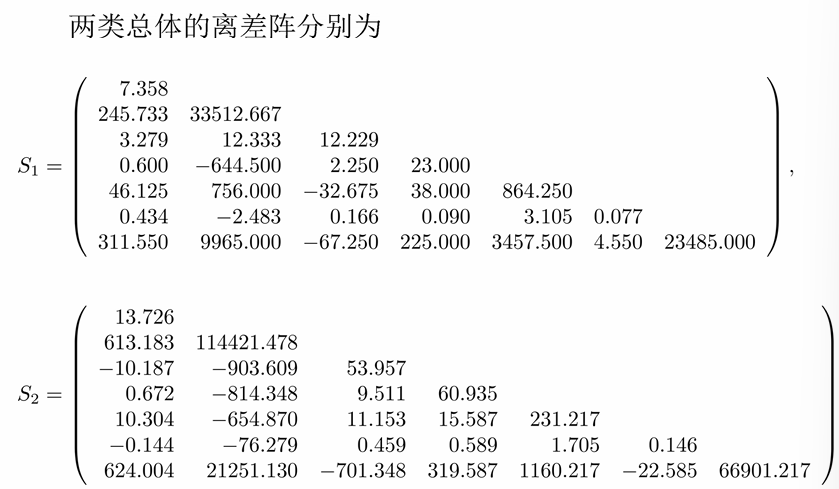
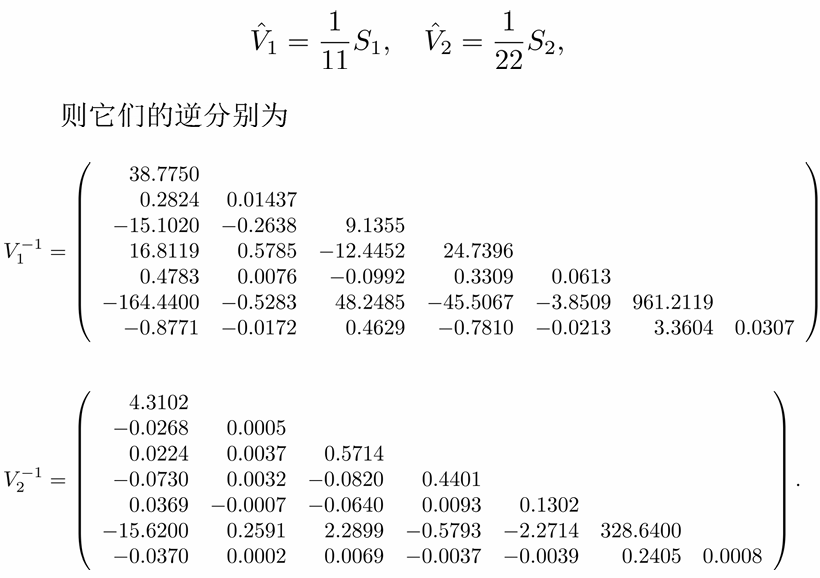
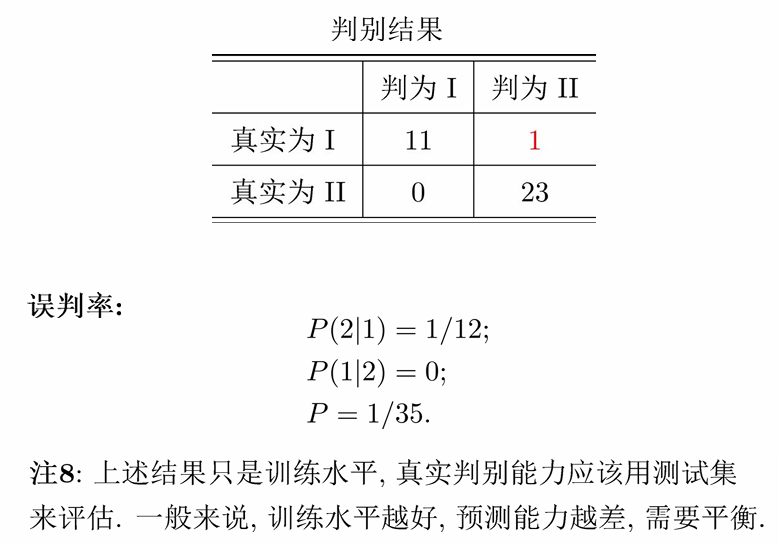
8.5 误判概率

考虑两个正态总体的情形. 分别为和。此时，距离判别、贝叶斯判别和Fisher判别等价判别函数为:

$W(y)=(y - \frac{\mu_1+\mu_2}{2})'V^{-1}(\mu_1 - \mu_2)$

记为样本来自而被误判为的概率，。则 :

$P(2|1)=P\{W(y)\leq d|G_1\}\\ P(1|2)=P\{W(y)>d|G_2\}$

其中为某个常数:

$d=\begin{cases}0, & \text{距离判别}\\ \log\frac{\pi_2L(2,1)}{\pi_1L(1,2)}, & \text{贝叶斯判别}\\ 0\text{或其它}, & \text{Fisher判别}\end{cases}$

8.5.1 误判概率：总体参数未知的情形

定理8.6 当和已知时，

$(W(y)|G_1)\stackrel{d}{\sim}N_1(\frac{a}{2},a)\\ (W(y)|G_2)\stackrel{d}{\sim}N_1(-\frac{a}{2},a)$

其中。

证明：是线性函数，因此它服从正态分布，且 :
$\begin{align} E(W(y)|G_1)&=(\mu_1 - \frac{\mu_1+\mu_2}{2})'V^{-1}(\mu_1 - \mu_2)\\&=\frac{1}{2}(\mu_1 - \mu_2)'V^{-1}(\mu_1 - \mu_2)\\&=\frac{1}{2}a\\\\Var(W(y)|G_1)&=[V^{-1}(\mu_1 - \mu_2)]'V[V^{-1}(\mu_1 - \mu_2)]\\&=(\mu_1 - \mu_2)'V^{-1}(\mu_1 - \mu_2)\\&=a \end{align}$
即知。同理可知:
$(W(y)|G_2)\stackrel{d}{\sim}N_1(-\frac{a}{2},a)$

推论8.7 当和已知时，误判概率为:

$P(2|1)=P\{W(y)\leq d|G_1\}=\Phi(\frac{d - \frac{a}{2}}{\sqrt{a}})\\ P(1|2)=P\{W(y)>d|G_2\}=1 - \Phi(\frac{d+\frac{a}{2}}{\sqrt{a}})$

“d”的确定：

误判概率最小化：即要求:
$\Phi(\frac{d - \frac{a}{2}}{\sqrt{a}})=1 - \Phi(\frac{d+\frac{a}{2}}{\sqrt{a}})$
方程的解为，与距离判别一致。
误判损失最小化：即要求:
$L(1,2)\Phi(\frac{d - \frac{a}{2}}{\sqrt{a}})=L(2,1)[1 - \Phi(\frac{d+\frac{a}{2}}{\sqrt{a}})]$
求解方程即可得。
注9：由式知，越大，误判概率越小。越大，与的马氏距离越大，即两个总体越分得开。

类似地，基于训练样本可得判别函数:

$W(y)=(y - \frac{\bar{y}_1+\bar{y}_2}{2})'\hat{V}^{-1}(\bar{y}_1 - \bar{y}_2)$

定理8.8 有如下极限分布:

$(W(y)|G_1)\stackrel{d}{\rightarrow}N_1(\frac{a}{2},a)(\min(n_1,n_2)\rightarrow\infty)\\ (W(y)|G_2)\stackrel{d}{\rightarrow}N_1(-\frac{a}{2},a)(\min(n_1,n_2)\rightarrow\infty)$

由定理8.8可得如下误判概率的估计:

$\hat{P}(2|1)=\Phi(\frac{d - \hat{a}}{\sqrt{\hat{a}}}),\ \hat{P}(1|2)=1 - \Phi(\frac{d+\hat{a}}{\sqrt{\hat{a}}})$

其中。

还可以利用的无偏估计来估计误判概率和:

$\tilde{a}=\frac{n_1 + n_2 - m - 1}{n_1 + n_2 - 2}\hat{a}-\frac{mn_1n_2}{n_1 + n_2}$

基于误判概率估计，可以使误判概率极小化来确定。

进一步，可以由的条件渐近分布的高阶近似公式，得到误判概率更精确的估计，进而确定最优判别准则。

8.5.2 基于误判概率的判别方法

假设正态，基于误判概率, 适用面窄

考虑的贝叶斯情形，和是先验概率，。

那么平均误判概率为:

$P=\pi_1P(2|1)+\pi_2P(1|2)$

以正态总体和，以及线性判别函数为例。判别规则为:

$\begin{cases}y\in G_1, & \text{若}\alpha(y)\geq d\\ y\in G_2, & \text{若}\alpha(y)<d\end{cases}$

不难计算得:

$P(2|1)=P\{W(y)\leq d|G_1\}=\Phi\left(\frac{d - u_1}{v_1}\right)\\ P(1|2)=P\{W(y)>d|G_2\}=1 - \Phi\left(\frac{d - u_2}{v_2}\right)$

求解和，使得平均误判概率达到极小。

$P = \pi_1\Phi\left(\frac{d - u_1}{v_1}\right)+\pi_2\left[1 - \Phi\left(\frac{d - u_2}{v_2}\right)\right]$

多元统计分析-Ch8-判别分析