Ch7 因子分析

一只码字机踩过…

时间远远不够です、どうしますか…

[TOC]

7.1 引入

因子分析法：

在多变量分析中，某些变量间往往存在相关性。

Q1: 是什么原因使变量间有关联呢？

Q2: 是否存在不能直接观测到的，但影响可观测变量变化的公共因子？

因子分析法就是寻找这些公共因子的模型分析方法。通过构建若干意义较为明确的公共因子，以它们为框架分解原变量，以此考察原变量间的联系与区别。

因子分析的目的和应用：

目的：用有限个不可观测的隐变量来解释原始变量之间的相关关系，是一种把多个变量化为少数几个综合变量的多变量分析方法。
主要应用 ：
- 减少分析变量个数。
- 通过对变量间相关关系的探测，将原始变量进行分类，即可以将相关性高的变量分为一组，并用共性因子代替该组变量。

7.1.1 例1: Spearman因素分析

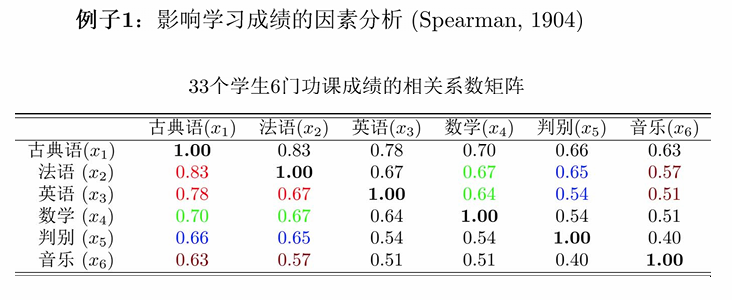
Spearman推测的解释：

因为相关系数矩阵是对称的，所以行=列。那么此处以列说明：每列基本上的相关系数值都差不多，所以任一两个值的比也都差不多。

的结果与无关，说明所有变量的相关性可以通过共同因子解释。

这个推测为 因子分析 提供了理论依据，即变量间的相关性具有内在结构。

其中，是一维的公共变量；是相互独立的随机变量，方差分别是；与独立，。

记，，，则模型可写为：

$X = af + U$

或:

$x_{i}=a_{i}f + u_{i},\ 1\leq i\leq 6$

A. Spearman模型的解释

每一门功课的成绩都由两部分组成: .
- 前一部分中的是对所有课程的成绩都有贡献的随机变量；
- 后一部分中是仅对第门课程的成绩有贡献的随机变量。
- 因此，称为公共因子，称为特殊因子。
因子载荷：称为第门课程成绩的因子载荷，理解为公共因子对第门课程成绩的作用程度。
公共因子含义: 可以理解为学生的阅读能力。
- 由于不同人的阅读能力有差异，故它是一个随机变量。
- 阅读能力对不同课程的贡献率不一样。

结论：Spearman模型是最早的仅有一个公共因子的因子模型。此模型就是在发现学生6门功课成绩的相关性后，挖掘出影响学习成绩的公共因子，并解释其对学习成绩影响的因子分析模型。

7.1.2 例2: 顾客感知因子模型

潜变量定义：

潜变量
说明	顾客对质量的感知	顾客对价值的感知	顾客满意度	顾客抱怨	顾客忠诚度

观测变量与潜变量的关系：

意义	与潜变量关系	潜变量意义
分别表示顾客对质量、质量可靠性和质量满足需求程度的评价	与有关	对质量感知
分别表示给定价格后顾客对质量的评价和给定质量后顾客对价格的评价	与有关	对价值的感知
分别表示顾客对企业的总评价、感知的质量与期望的比较，以及感知的质量与理想中的质量的差距	与有关	顾客满意度
表示顾客正式或非正式的投诉行为对质量的评价和给定质量后顾客对价格的评价	与有关	顾客抱怨
分别表示顾客重复购买的可能性，顾客可承受的涨价幅度或促销（降价）对顾客购买的影响	与有关	顾客忠诚度

7.1.3 因子分析模型

记观察变量, 公共因子, 特殊因子.

假设：

相互独立，且。
相互独立，且。
与相互独立。
。

记因子载荷矩阵，描述因子与观测变量之间的关系. 那么上述的模型可以一般化为:

$x_i=\sum_{j = 1}^{m}a_{ij}f_j + u_i, 1\leq i\leq p\\ 1 = Var(x_i)=\sum_{j = 1}^{m}a_{ij}^2+\sigma_i^2, 1\leq i\leq p$

记，则有.

称为公共因子对的贡献(or say 变量的公共方差)，它反映公共因子对的影响；是特殊因子对变量的贡献(or say 变量的特殊方差)。

越大则越小，反之亦然，说明变量对公共因子和特殊因子的依赖此消彼长。

公共因子对的贡献

公共因子对的贡献可以表示为：

$g_j^2=\sum_{i = 1}^{p}a_{ij}^2$

是公共因子的方差贡献总和，表示对所有变量的总体影响程度。，越大，说明对的影响越大，也就越重要。

对任意, 有:

$Cov(x_i, f_j)=\sum_{k = 1}^{m}a_{ik}Cov(f_k, f_j)+Cov(u_i, f_j)=a_{ij}=\rho(x_i, f_j)$

因此，因子载荷矩阵的统计意义为：

是与的相关系数。
是对公共因子的依赖程度。
是公共因子对的各个分量的影响总和。

7.2 正交因子模型

正交因子模型：令, .

具有因子结构(与相互独立):


维常数向量	阶常数矩阵
	因子载荷矩阵	公共因子	特殊因子

$\text{Cov}(x)=\Sigma = AA^{\prime}+D$

注意：因子载荷矩阵并不唯一，因为对任意阶正交矩阵，有:
$\begin{align}x&=\mu + Af + u\\ &=\mu+(AT)(T^{\prime}f)+u\\ &=\mu+(AT)f^{*}+u\\\\ f^{*}&=T^{\prime}f\sim N_{m}(0, I_{m})\\ \text{Cov}(x)&=AA^{\prime}+D=(AT)(AT)^{\prime}+D \end{align}$

7.2.1 因子载荷矩阵的表示

Q: 在给定的相关阵和对角阵的条件下，如何求解？

约相关阵：

易知，的对角元素为，，其它元素与一样，且非负定。

$R^*=AA'=\begin{pmatrix} a_{11}&a_{12}&\cdots&a_{1m}\\ a_{21}&a_{22}&\cdots&a_{2m}\\ \vdots&\vdots&\ddots&\vdots\\ a_{p1}&a_{p2}&\cdots&a_{pm}\\ \end{pmatrix}\begin{pmatrix} a_{11}&a_{21}&\cdots&a_{p1}\\ a_{12}&a_{22}&\cdots&a_{p2}\\ \vdots&\vdots&\ddots&\vdots\\ a_{1m}&a_{2m}&\cdots&a_{pm}\\ \end{pmatrix}\\ R^*_{ii}=A_{i*}·A_{i*}'=\sum^m_{j=1}a_{ij}^2=h_{i}^2\\ R^*_{ij}=A_{i*}·A_{j*}'=\sum^m_{k=1}a_{ik} a_{jk}$

记$R^ $内的元素为$ r^_{ij}=\sum^m_{k=1}a_{ik} a_{jk},\ 1\le j,k\le p$.

目标：求解的各列，使得“贡献”.

要求：使得达到最大值的解。

利用特征根和特征向量求解:

记为的特征根，其对应的正则正交特征向量分别为。则 :

$\begin{align}R^{*}&=U\Lambda U'=U\Lambda^{\frac 1 2} U'=AA' \\&=(\alpha_{1},\cdots,\alpha_{p})\text{diag}(\lambda_{1},\cdots,\lambda_{p})(\alpha_{1},\cdots,\alpha_{p})^{\prime}\\ &=(\alpha_{1},\cdots,\alpha_{p})\text{diag}(\sqrt{\lambda_{1}},\cdots,\sqrt{\lambda_{p}})\text{diag}(\sqrt{\lambda_{1}},\cdots,\sqrt{\lambda_{p}})(\alpha_{1},\cdots,\alpha_{p})^{\prime}\\\\ A &= (\alpha_{1},\cdots,\alpha_{m})\text{diag}(\sqrt{\lambda_{1}},\cdots,\sqrt{\lambda_{m}}) \end{align}$

其中是的秩。

7.3 因子载荷矩阵的估计

7.3.1 R主成分估计法

认为比较粗糙，一般对$R^=R-D$进行主成分分析，此处*直接对R进行主成分分析。

记为样本相关阵。对做谱分解有 :

$\hat{R}=\sum_{i = 1}^{p}\hat{\lambda}_{i}\hat{\alpha}_{i}\hat{\alpha}_{i}'$

其中，。

先取，然后看是否接近对角阵。

如果接近对角阵，表明剩下的都是特殊因子的影响，只有一个公共因子。
否则一直进行下去。

实际操作中，给定一个阈值，若:

$\frac{\sum_{i = 1}^{m}\hat{\lambda}_{i}}{\sum_{i = 1}^{p}\hat{\lambda}_{i}}\geq\delta$

则取 :

$\hat{\Lambda}=(\hat{a}_{1},\cdots,\hat{a}_{m})\text{diag}(\sqrt{\hat{\lambda}_{1}},\cdots,\sqrt{\hat{\lambda}_{m}})=(\sqrt{\hat{\lambda}_{1}}\hat{\alpha}_{1},\cdots,\sqrt{\hat{\lambda}_{m}}\hat{\alpha}_{m})$

7.3.2 MSE-极大似然估计法

假设是来自正交因子模型的独立观测样本，，则的似然函数为 :

$L(\mu,A,D)=\vert AA'+D\vert^{-n/2}\exp\left\{-\frac{n}{2}\text{tr}[(AA'+D)^{-1}(S + (\bar{x}-\mu)(\bar{x}-\mu)')]\right\}$

其中，是样本均值，是样本协差阵。

对求极大后得的对数似然函数为 :

$L(A,D)=|AA'+D|^{-\frac n 2} \exp\{-\frac n2tr\left[(AA'+D)^{-1}S)\right]\}\\ \ln L(A,D)=l(A,D)=-\frac n2\ln|AA'+D|-\frac n2tr\left[(AA'+D)^{-1}S)\right]$

对其求偏微分、极大似然估计满足：

$\begin{cases} \frac{\partial l(\hat{A},\hat{D})}{\partial A}=0;\\\frac{\partial l(\hat{A},\hat{D})}{\partial D}=0\\ \end{cases}$

求解过程如下：

因此，第一项关于 AA 的偏导数为：
$\frac{\partial}{\partial A} \left( -\frac{n}{2} \ln |AA' + D| \right) = -\frac{n}{2} \cdot (AA' + D)^{-1} \cdot \frac{\partial (AA' + D)}{\partial A}\\ \because\frac{\partial (AA')}{\partial A} = A\\ \therefore\frac{\partial}{\partial A} \left( -\frac{n}{2} \ln |AA' + D| \right) = -\frac{n}{2} (AA' + D)^{-1} A\\$
矩阵的迹的偏导性质为：
$\because\frac{\partial \text{tr}(A^{-1} B)}{\partial A} = -A^{-1} B A^{-1}\\\therefore\begin{align} \frac{\partial}{\partial A} \left( -\frac{n}{2} \text{tr} \left[ (AA' + D)^{-1} S \right] \right)& = -\frac{n}{2} \cdot \left[ - (AA' + D)^{-1} S (AA' + D)^{-1} \right] \cdot \frac{\partial (AA' + D)}{\partial A}\\ &= \frac{n}{2} (AA' + D)^{-1} S (AA' + D)^{-1} A\end{align}$
将两项的偏导数相加，得到：
$\frac{\partial l(A, D)}{\partial A} = -\frac{n}{2} (AA' + D)^{-1} A + \frac{n}{2} (AA' + D)^{-1} S (AA' + D)^{-1} A=0\\ -\frac{n}{2} (AA' + D)^{-1} A \left[ I - (AA' + D)^{-1} S \right]=0\\$
由于是非奇异矩阵，且，所以要求：
$I - (AA' + D)^{-1} S = 0\\ (AA' + D)^{-1} S = I\\ S=(AA'+D)$
而对求解，结果也是

根据我们计算偏导的结果，能够知道极大似然估计满足下面的方程组：：

$\begin{cases} A=S(AA'+D)^{-1}A\quad &\text{(因子载荷矩阵的更新方程)}\\ diag(S)=diag(AA'+D)\quad &\text{(对角元素方差约束)} \end{cases}$

A. 其他表示

Q: 进行变换有何意义？

A: GPT大爷如是说到——

解耦和标准化：

通过引入和，将原始因子分析模型中的协方差分解标准化，减少了特殊方差 D 对求解的影响。

变换后的方程更简洁，特别是在数值迭代计算中，便于求解。

结构性分解：

方程和标准化方程提供了一个明确的框架，展示了样本协方差矩阵与因子载荷之间的关系。

数值求解的基础：

在实际应用中，这些变换是迭代估计算法（如极大似然估计和 EM 算法）的基础。

归一化后的方程可以用于更新 A 和 D，直到收敛。

由：

$\begin{align}A(I_m+A'D^{-1}A)&=A+AA'D^{-1}A,\quad I_m=DD^{-1}\\ A(I_m+A'D^{-1}A)&=DD^{-1}A+AA'D^{-1}A\\&=(D+AA')D^{-1}A\\\\ A(I_m+A'D^{-1}A)&=(D+AA')D^{-1}A\\ A&=(D+AA')D^{-1}A(I_m+A'D^{-1}A)^{-1}\\ (D+AA')^{-1}A&=D^{-1}A(I_m+A'D^{-1}A)^{-1} \end{align}$

因为, 对A代换有:

$A=S(AA'+D)^{-1}A=SD^{-1}A(I_m+A'D^{-1}A)^{-1}\\ A=SD^{-1}A(I_m+A'D^{-1}A)^{-1}\\ SD^{-1}A=A(I_m+A'D^{-1}A)$

上述的解可以被写成：

$\begin{cases} SD^{-1}A=A(I_m+A'D^{-1}A)\\ diag(S)=diag(AA'+D) \end{cases}$

上面的方程还可以被写成：
$SD^{-1}A=A(I_m+A'D^{-1}A)\\ D^{-\frac 1 2}SD^{-1}A=(D^{-\frac 1 2}A)(I_m+A'D^{-1}A)\\ (D^{-\frac 1 2}SD^{-\frac 1 2})(D^{-\frac 1 2}A)=(D^{-\frac 1 2}A)(I_m+A'D^{-1}A)$

B.因子载荷矩阵的唯一解

注意到：因子负荷矩阵不唯一。

这是因为对任意正交矩阵成立。由于正交矩阵有:

$m^2 - m - m(m - 1)/2=m(m - 1)/2$

个变量(自由度)。

因此，为使的解“唯一”，需对加上个约束。对的约束为 :

$A'D^{-1}A=\Gamma=\text{diag}(\gamma_{1},\cdots,\gamma_{m})>0$

如果加上约束条件：，则由方程推知：

$\begin{align}(D^{-\frac{1}{2}}SD^{-\frac{1}{2}})(D^{-\frac{1}{2}}A)&=(D^{-\frac{1}{2}}A)(I_{m}+A'D^{-1}A)\\ (D^{-\frac{1}{2}}SD^{-\frac{1}{2}})(D^{-\frac{1}{2}}A)&=(D^{-\frac{1}{2}}A)(I_{m}+\Gamma)\\ (D^{-\frac{1}{2}}SD^{-\frac{1}{2}})(D^{-\frac{1}{2}}A)\Gamma^{-\frac 1 2}&=(D^{-\frac{1}{2}}A)(I_{m}+\Gamma)\Gamma^{-\frac 1 2}\\ (D^{-\frac{1}{2}}SD^{-\frac{1}{2}})(D^{-\frac{1}{2}}A)\Gamma^{-\frac 1 2}&=(D^{-\frac{1}{2}}A)\Gamma^{-\frac 1 2}(I_{m}+\Gamma)\\ (D^{-\frac{1}{2}}SD^{-\frac{1}{2}})(D^{-\frac{1}{2}}A\Gamma^{-\frac 1 2})&=(D^{-\frac{1}{2}}A\Gamma^{-\frac 1 2})(I_{m}+\Gamma)\\\\ \because\Gamma^{-\frac 1 2}A'D^{-1}A\Gamma^{-\frac 1 2}=\frac{A'DA}{A'DA}&=I_m\\ \therefore(D^{-\frac{1}{2}}A\Gamma^{-\frac 1 2})'(D^{-\frac{1}{2}}A\Gamma^{-\frac 1 2}) &= I_{m} \end{align}$

表明下列例子成立：

$\begin{cases} (D^{-\frac{1}{2}}SD^{-\frac{1}{2}})(D^{-\frac{1}{2}}A\Gamma^{\frac 1 2})=(D^{-\frac{1}{2}}A\Gamma^{\frac 1 2}) (I_{m}+\Gamma)\\ (D^{-\frac{1}{2}}A\Gamma^{\frac 1 2})'(D^{-\frac{1}{2}}A\Gamma^{\frac 1 2}) = I_{m} \end{cases}$

表明是的个正特征根; 是它们对应的正则正交特征向量矩阵。

由于:

$D^{-\frac{1}{2}}\Sigma D^{-\frac{1}{2}}=D^{-\frac{1}{2}}(AA'+D)D^{-\frac{1}{2}}=(A'D^{-\frac{1}{2}})'(A'D^{-\frac{1}{2}})+I_{p}$

而与有相同的非零特征根。

因此的前个特征根为，其它全是。

在给定的条件下，可计算出的个非零特征根，以及它们对应的正则正交特征向量矩阵. 令。

则方程的解为:

$D^{-\frac{1}{2}}A\Gamma^{-\frac{1}{2}}=E\\\Rightarrow A = D^{\frac{1}{2}}E\Gamma^{\frac{1}{2}}$

C.MSE迭代算法

给出的一个初始估计: 可由主成分法等确定的一个粗估计，或简单地由各分量的方差估计作为初始估计。记。
计算特征根和特征向量并估计因子载荷矩阵: 计算的前个特征根以及它们所对应的正则正交特征向量。记:
$\Gamma_1 = \text{diag}(\lambda_{1,1}-1,\cdots,\lambda_{1,m}-1)\\ E_1=(e_{1,1},\cdots,e_{1,m})\\ A_1 = D_0^{\frac{1}{2}}E_1\Gamma_1^{\frac{1}{2}}$
是因子载荷矩阵的估计，这里要求，否则减小，或停止。
给出的迭代估计 - 由方程(2)给出的迭代估计:
$D_1=\text{diag}(S)-\text{diag}(A_1A_1')$
这里要求，否则停止。
迭代循环 - 返回(1)，直至迭代停止。

也可以使用EM算法，视作隐变量进行计算。

7.4 因子旋转

由于因子载荷矩阵不唯一，因此可以寻找一个正交矩阵使得对应的公共因子具有更好的实际意义而便于解释

7.4.1 方差最大的正交旋转(Varimax旋转)

先考虑两个因子的正交旋转，设因子载荷矩阵和正交矩阵为：

, T是旋转矩阵。

令

$\begin{cases} b_1=a_1\cos(\varphi)-a_2\sin(\varphi)\\ b_2=a_1\sin(\varphi)+a_2\cos(\varphi) \end{cases}$

目标：旋转后，因子的“贡献”越分散越好。

结果：可分为两部分，一部分主要与第一因子有关，另一部分主要与第二因子有关。

定义和的相对方差：

$V_i(\varphi)=\frac 1 p\sum^p_{j=1}\left(\frac{b_{ji}^2}{h_j^2}\right)-\left(\frac 1 p\sum^p_{j=1}\frac{b_{ji}^2}{h_j^2}\right)^2$

其中表示因子对的影响；要求使得总方差最大，即求：

$\hat\varphi=\arg\max_{\varphi}(V_1(\varphi)+V_2(\varphi))$

记：()

此法具有显式解：

$\tan(4\hat\varphi)=\frac{D-2\frac{AB}{p}}{C-\frac{A^2-B^2}{p}}$

进而得正交矩阵：

$T=\begin{pmatrix}\cos(\hat\varphi)&-\sin(\hat\varphi)\\ \sin(\hat\varphi)&cos(\hat\varphi) \end{pmatrix}$

取得的方差是有界（其成分都是有界的）、故一定会收敛。

在旋转的同时，都会更接近收敛（比原来好），因此到达停止条件的时候，收敛。

7.4.2 更多公共因子的情形

当公共因子个数时，可以逐次对每两个公共因子对进行Varimax旋转。

自然而然地联想到矩阵分解方法：Givens reduction(√)

这样做次后，所有公共因子对都旋转一次，记为旋转一轮。如果旋转一轮后未达到目标，再进行新一轮旋转。记第次旋转后因子载荷矩阵的相对方差差总和为，

$G^{(j)}=\sum_{i = 1}^{m}V_{i}^{(j)}$

由Varimax的性质知，

而因子载荷矩阵的元素绝对值均不大于1，因此上述单调序列有上界，故收敛。

实际中，若认为因子载荷矩阵的相对方差差总和已经变化很小时，则停止旋转。

7.5 正交因子模型协方差结构的检验

在因子分析中，正交因子模型假设观测变量的协方差矩阵可以被分解为因子载荷矩阵和特殊方差矩阵的组合形式：

$\Sigma = AA' + D$

模型假设的是一个特定的协方差结构，但这个假设不一定总是成立，因此需要检验协方差的结构是否符合模型的理论假设。

检验协方差结构的目的和意义:

理论协方差矩阵 是因子模型根据参数 A 和 D 推导得到的。

实际协方差矩阵 S 是根据样本数据计算出来的。

目标是检验实际协方差矩阵 S 是否与理论协方差矩阵足够接近。

如果，说明因子模型合理，协方差的结构假设成立；

如果与偏差较大，说明因子模型可能不适合当前数据。

7.5.1 正交因子模型极大似然估计相关推导

设是来自总体的样本，其中，。

有关正交因子模型的检验问题为:

$H_0:\Sigma = AA'+D$

其中是秩为的矩阵，。

记的极大似然估计为，则有:

$L(\hat{A},\hat{D})=\vert\hat{A}\hat{A}'+\hat{D}\vert^{-n/2}\exp\left\{-\frac{n}{2}\text{tr}[(\hat{A}\hat{A}'+\hat{D})^{-1}S]\right\}$

由于极大似然估计满足似然方程，故有:

$\begin{cases} \hat{A}=S(\hat{A}\hat{A}'+\hat{D})^{-1}\hat{A}\\ \text{diag}(S)=\text{diag}(\hat{A}\hat{A}'+\hat{D}) \end{cases}$

对任意方阵和正定的对角阵，有:

$\text{tr}[\text{diag}(QP)]=\text{tr}[QP]=\text{tr}[(\text{diag}(Q))P]$

由是对角阵与方程可知:

$\begin{align} tr\left[(S-\hat A\hat A')\hat D^{-1}\right]&=tr\left[diag\left((S-\hat A\hat A')\hat D^{-1}\right)\right]\\ &=tr\left[\left(diag(S-\hat A\hat A')\right)\hat D^{-1}\right]\\\\ \because \text{diag}(S)&=\text{diag}(\hat{A}\hat{A}'+\hat{D})\\ \therefore \text{diag}(S)&=\text{diag}(\hat{A}\hat{A}')+diag(\hat{D})\\\\ tr\left[(S-\hat A\hat A')\hat D^{-1}\right]&=tr\left[diag(\hat D)\hat D^{-1}\right]\\ &=trtr\left[diag(\hat D\hat D^{-1})\right]\\ &=p \end{align}$

根据知：

$\begin{align} tr\left[S(\hat A\hat A'+\hat D)^{-1}\right]&=tr\left[S(\hat A\hat A'+\hat D)^{-1}(\hat A\hat A'+\hat D-\hat A\hat A')\hat D^{-1}\right]\\ &=tr\left[S\left(\hat D^{-1}-(\hat A\hat A'+\hat D)^{-1}\hat A\hat A'\hat D^{-1}\right)\right]\\ &=tr\left[S\hat D^{-1}-\left(S(\hat A\hat A'+\hat D)^{-1}\hat A\right)\hat A'\hat D^{-1}\right]\\ &=tr\left[S\hat D^{-1}-\hat A\hat A'\hat D^{-1}\right]\\ &=tr\left[\left(S-\hat A\hat A'\right)\hat D^{-1}\right]\\ &=p \end{align}$

因此有：

$L(\hat A,\hat D)=\vert\hat A\hat A'+\hat D\vert^{-\frac n 2}\exp\{-\frac {np}2\}$

正交因子模型检验的似然比为：

$\begin{align} \lambda&=\frac{\sup_{\mu,\Sigma = AA'+D}\vert\Sigma\vert^{-n/2}\exp\left\{-\frac{n}{2}\text{tr}[\Sigma^{-1}(S + (\bar{x}-\mu)(\bar{x}-\mu)')]\right\}}{\sup_{\mu,\Sigma}\vert\Sigma\vert^{-n/2}\exp\left\{-\frac{n}{2}\text{tr}[\Sigma^{-1}(S + (\bar{x}-\mu)(\bar{x}-\mu)')]\right\}}\\ &=\left(\frac{\vert S\vert}{\vert\hat{A}\hat{A}'+\hat{D}\vert}\right)^{n/2} \end{align}$

计算参数空间的自由度:

由于为对角阵，即有个约束。因此
自由度为：

由Wilks定理知：

$- 2\ln\lambda=-n(\ln S-\ln\vert\hat{A}\hat{A}'+\hat{D}\vert)\stackrel{d}{\rightarrow}\chi^2(f)$

检验方案: 当时拒绝零假设，其犯第一类错误的概率近似为。

正交因子模型的识别性问题: 当自由度时，正交因子模型存在可识别性问题。

当时，分解不唯一;（偏大）

当时，分解或不存在，或存在唯一。

7.6斜交旋转

设维随机向量可以表示为：

$\mathbf{x}=\mu + A\mathbf{f}+\mathbf{u}$

其中，是维常数向量，是阶常数矩阵，，，为相关阵，，，与相互独立。

称模型为斜交因子模型，称为公共因子，为特殊因子，为因子载荷矩阵。

Actually，存在满秩阵，使得。若令，，则：

$\begin{align} {x}&=\mu + \mathbf A{f}+{u}\\ &=\mu+(\mathbf AT)(T^{-1}{f})+{u}\\ &=\mu+\mathbf Bg+u \end{align}$

易知:

$$\text{Cov}(\mathbf{g})=T^{-1}\text{Cov}(\mathbf{f})(T^{\prime})^{-1}=T^{-1}R(T^{\prime})^{-1}=I_{m}$

则是正交因子模型，是公共因子，是正交因子载荷矩阵。

由于非正交矩阵，我们称公共因子为正交公共因子的斜交旋转。

7.7 因子得分

将因子表示成变量的线性组合（反代）

, 其中是公共因子, 是变量。

因子得分函数：
因子得分矩阵：

由因子得分函数知:

$f_j=\sum_{i = 1}^{p}b_{ji}x_i, \quad 1\leq j\leq m$

7.7.1 因子得分的计算—计算因子得分矩阵

假定变量已作标准化处理，即，，。令，也是的相关阵。记。

假定因子载荷矩阵和相关阵已知。

对任意，，有：

$\begin{align} a_{ij}&=E(x_if_j)\\&=\sum_{k = 1}^{p}b_{jk}E(x_ix_k)\\&=\sum_{k = 1}^{p}r_{ik}b_{jk} \end{align}$

因此对，有：

$\begin{pmatrix} r_{11}&r_{12}&\cdots&r_{1p}\\ r_{21}&r_{22}&\cdots&r_{2p}\\ \vdots&\vdots&\ddots&\vdots\\ r_{p1}&r_{p2}&\cdots&r_{pp} \end{pmatrix} \begin{pmatrix} b_{j1}\\ b_{j2}\\ \vdots\\ b_{jp} \end{pmatrix} = \begin{pmatrix} a_{1j}\\ a_{2j}\\ \vdots\\ a_{pj} \end{pmatrix}$

7.7.2 估计(因子载荷矩阵)—回归法

因子载荷矩阵估计：，相关阵估计：.

因子得分矩阵

$\begin{pmatrix} \hat{b}_{j1}\\ \hat{b}_{j2}\\ \vdots\\ \hat{b}_{jp} \end{pmatrix} =\hat{R}^{-1} \begin{pmatrix} \hat{a}_{1j}\\ \hat{a}_{2j}\\ \vdots\\ \hat{a}_{pj} \end{pmatrix}, \quad 1\leq j\leq m,$

则因子得分估计为

因子得分：

判断公共因子的重要度：得分高，更重要。
样本聚类：可以使用因子得分对样本进行聚类（但不是唯一）。

7.8 PCA与因子分析

本质：寻找一个低秩矩阵，使其无限接近于原矩阵。

因子需要考虑对角阵，主成分考虑范数。

因子LS(Least Square)估计(不需要正态)：

可以使用MSE计算：

$s.t.\begin{cases} \Phi\ge 0, \quad rank(\Phi)=k\\ D\gt 0,diag. \end{cases}$

迭代训练：

，得到前m个主成分。

不一定是正态的时候使用，但是是正态的时候还是MSE更优。==证明？==

因子也是HMM。

7.8.1 EM-模式识别作业参考

对混合高斯模型参数估计问题，在EM优化的框架下，请给出其中的的基本形式。

解：

E-step: 固定当前参数，对每个样本求。

$P(z_{i}|\mathbf{x}_{i},\mathbf{\theta}^{\text{old}}) = \frac{p(\mathbf{x}_{i}, z_{i} \mid \mathbf{\theta}^{\text{old}})}{p(\mathbf{x}_{i} \mid \mathbf{\theta}^{\text{old}})} = \frac{\pi_{z_{i}} \mathcal{N}(\mathbf{x}_{i} \mid \mathbf{\mu}_{z_{i}}, \mathbf{\Sigma}_{z_{i}})}{\sum_{k=1}^{K} \pi_{k} \mathcal{N}(\mathbf{x}_{i} \mid \mathbf{\mu}_{k}, \mathbf{\Sigma}_{k})}$

M-step: 固定，通过更新参数。

$\begin{aligned} Q(\mathbf{\theta}, \mathbf{\theta}^{\text{old}}) &= \sum_{i} \sum_{z_{i}=1}^{K} p(z_{i}|\mathbf{x}_{i}, \mathbf{\theta}^{\text{old}}) \ln \pi_{z_{i}} \\ &\quad + \sum_{k=1}^{K} \sum_{i} p(z_{i} = k | \mathbf{x}_{i}, \mathbf{\theta}^{\text{old}}) \ln \mathcal{N}(\mathbf{x}_{i} | \mathbf{\mu}_{k}, \mathbf{\Sigma}_{k}) \end{aligned}$

多元统计分析-Ch7-因子分析