多元统计分析-Ch6-主成分分析

Ch6 主成分分析

[TOC]

目的：根据二八定律（雾），大量有效的信息都在很少的指标中。所以PCA在尽量减少损失信息的前提下，将多个指标降维，综合成几个综合指标。

总的来说，PCA就是数据降维。但需要注意的是，得到的降维后的变量无实际意义（基本上就是原各个变量都混合一点的“大杂烩”）。

思路：选取变量的线性组合，使其（使得这个线性组合的方差尽可能的大，接近各个分类的方差之和，进而代表总体的散布程度）。

[TOC]

6.0 引入

6.0.1 例子

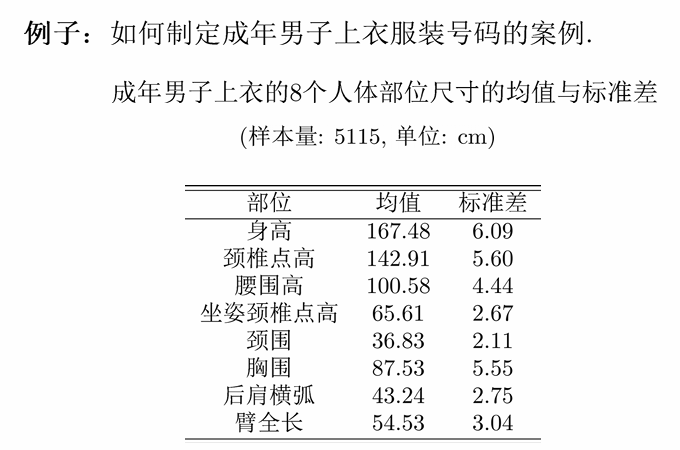
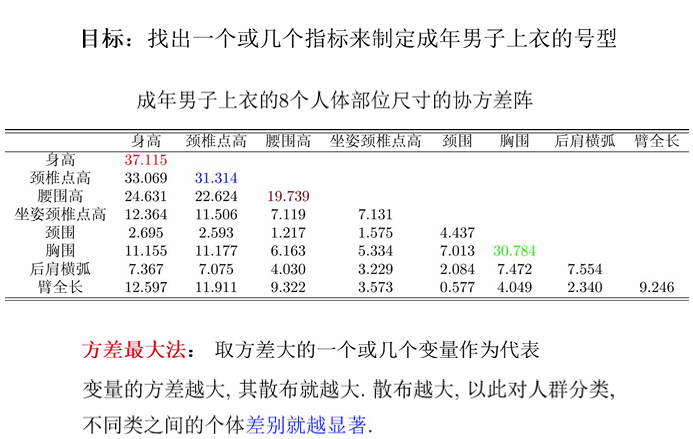
方差,选取的是对角线上值最大的前四个。

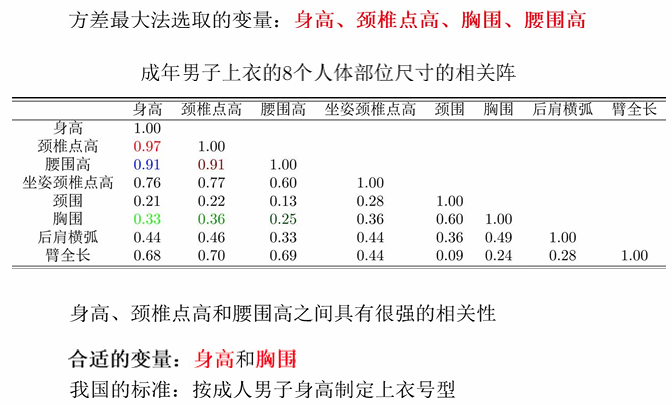
计算相关系数：, 我们选择的方差最大的四个变量中，身高与颈椎点高、腰围高之间相关性交，所以只取身高即可。

最终选取的变量是：身高和胸围。

但仍存在问题：身高和胸围仍然具有相关性，应该对其进行进一步地压缩，以选出更具有代表性的指标。

Q：是否有更具代表性一个or少数指标

代表性标准：方差最大。

6.0.2 主成分分析

记是维随机向量()，我们想基于，找到变量(的线性组合)，令的方差尽可能地大，足以代表的散布。

因为，这表明若不对施加约束，则的最大方差。

所以对施加正则化约束：，使得优化问题为：

$$\sup_{a'a=1}Var(a'X)=\sup_{a'a=1} a'\Sigma a$$

令, 是的第一主成分。

• 是正则化系数下方差最大的的线性组合。
• 的散布程度最接近, 是代表的首选。

A.总体协方差矩阵的特征根与特征向量

首先，我们先回顾一下URV分解、SVD分解、Moore-Penrose伪逆：

令的特征根为，与这些特征根对应的正则正交特征向量为。 易知:

$$\alpha_{1}=\alpha_{1}=(a_{11},\cdots,a_{1p})'\\ V_{ar}(a_{1}'X)=a_{1}'\Sigma a_{1}=\lambda_{1}$$

则第一主成份：

• 方向：总体协差阵的最大特征根所对应的正则特征向量。
• 方差：总体协差阵的最大特征根。

B.随机向量的离散程度

设维随机向量，其离散程度的信息可用向量各分量方差的总和表示：

$$V{ar}(x_{1})+\cdots+V{ar}(x_{p})$$

第一主成份的作用 ：

将所含离散程度的信息最大化地用一个线性组合变量所含离散程度的信息来代替。

第一主成份离散程度信息的贡献率：

$$\text{contriution}=\frac{V{ar}(a_{1}'X)}{\sum_{i = 1}^{p}V{ar}(x_{i})}\times100\%$$

Q：第一主成份代表性是否足够？或第一主成份贡献率是否足够？

A: 寻找第二主成份, 第二主成份应该与第一主成份正交，从而不含有第一主成份的信息。优化问题如下：

$$\sup_{a_{2}'a_{2}=1,\ a_{2}'a_{1}=0}V_{ar}(a_{2}'X)=\sup_{a_{2}'a_{2}=1,\ a_{2}'a_{1}=0}a_{2}'\Sigma a_{2}\\ s.t.\begin{cases} \text{正则化约束：}a_{2}'a_{2}=1\\ \text{正交化约束：}a_{2}'a_{1}=0 \end{cases}$$

不难知道，，。

即，第二主成份:

• 方向：总体协差阵的第二大特征根所对应的正则特征向量；
• 方差：总体协差阵的第二大特征根。

第一主成份与第二主成份的正交性:

$$Cov(a_{1}'X,a_{2}'X)=a_{1}'\Sigma a_{2}=\lambda_{2}a_{1}'a_{2}=0$$

因此，正态总体下，第一主成份与第二主成份相互独立。

第二主成份离散程度信息的贡献率:

$$\text{contribution}=\frac{V_{ar}(a_{2}'X)}{\sum_{i = 1}^{p}V_{ar}(x_{i})}\times100\%$$

第一、第二主成份的累计贡献率:

$$\text{累计贡献率} = \frac{Var(a_1'X)+Var(a_2'X)}{\sum_{i = 1}^{p}Var(x_i)}×100\% \\$$

6.0.3 回到例子

因为是满秩的，那么是一个RPN阵，这个时候对它进行SVD分解，得到的U=V都是值域空间的标准正交基。

那么写一个简单的python程序，对进行SVD分解结果如下。

特征值&奇异值

序号	特征值	奇异值
1	10115.7573	100.5771
2	809.2391	28.4471
3	33.0498	5.7489
4	19.8222	4.4522
5	10.2260	3.1978
6	6.6843	2.5854
7	1.9138	1.3834
8	0.8612	0.9280

左奇异向量

元素
	-0.5920	0.1849	-0.1308	0.1612	-0.0062	-0.0136	-0.5614	0.5067
	-0.5469	0.1362	-0.0860	0.0608	-0.0676	-0.0599	-0.0709	-0.8112
	-0.4052	0.2028	0.2958	0.0702	0.5535	0.1070	0.5948	0.1752
	-0.2062	-0.0083	-0.4074	0.2113	-0.6080	-0.1179	0.5662	0.2065
	-0.0638	-0.2320	-0.1151	0.1003	-0.0726	0.9549	-0.0116	-0.0397
	-0.2680	-0.9003	0.2347	0.1167	0.0327	-0.2170	-0.0055	0.0272
	-0.1416	-0.1867	-0.6008	-0.7004	0.2935	-0.0286	0.0667	0.0472
	-0.2183	0.0831	0.5411	-0.6376	-0.4763	0.1055	0.0282	0.0854

右奇异向量 ()

元素
	-0.5920	-0.5469	-0.4052	-0.2062	-0.0638	-0.2680	-0.1416	-0.2183
	0.1849	0.1362	0.2028	-0.0083	-0.2320	-0.9003	-0.1867	0.0831
	-0.1308	-0.0860	0.2958	-0.4074	-0.1151	0.2347	-0.6008	0.5411
	0.1612	0.0608	0.0702	0.2113	0.1003	0.1167	-0.7004	-0.6376
	-0.0062	-0.0676	0.5535	-0.6080	-0.0726	0.0327	0.2935	-0.4763
	-0.0136	-0.0599	0.1070	-0.1179	0.9549	-0.2170	-0.0286	0.1055
	-0.5614	-0.0709	0.5948	0.5662	-0.0116	-0.0055	0.0667	0.0282
	0.5067	-0.8112	0.1752	0.2065	-0.0397	0.0272	0.0472	0.0854

通过成人男子8个身体部位尺寸的协方差阵知：

$$\lambda_{1}=100.5771\\ a_{1}=(0.5920,0.5469,0.4052,0.2062,0.0638,0.2680,0.1416,0.2183)'$$

第一主成份。

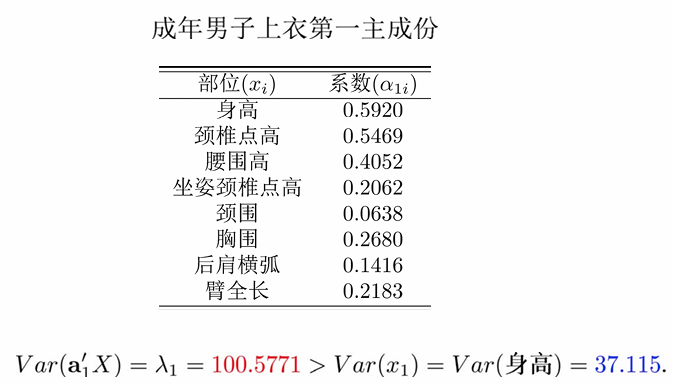
根据定理13.1.1 有：

$$\max_{a,b}\rho(a'X,b'Y)=\sqrt{\lambda_1}\\ Var(a'X)=\sqrt{\lambda_1}=100.57>Var(x_1)=37.115\\$$

第一主成份的方差(散布程度)更大。 将其作为成年男子上衣的第一基本特征更具有代表性，以此对人群进行划分将更细致。

国外确定服装号型：第一主成份。

成年男子上衣第一主成份的贡献率。

通过成人男子8个身体部位尺寸的协方差阵知：

$$\lambda_{2}=28.4471\\ a_{2}=(0.1849,0.1362,0.2028,-0.0083,-0.2320,-0.9003,-0.1867,0.0831)'$$

第二主成份。

对于成年男子上衣，有：

$$\text{累计贡献率} = \frac{129.0242}{147.32}×100\% = 87.6\%$$

Q1：第一、第二主成份代表性是否足够？

Q2：停止？还是类似地继续寻找更多的主成份？

6.1 总体PCA

设。令的特征根为，特征根对应的正则正交特征向量为。

令，则是正交阵，且:

$$T'\Sigma T=\Lambda, \quad \Lambda = diag(\lambda_1, \cdots, \lambda_p)$$

1. 令，，则称为的主成份. 令，则:

   • 的第主成份:
   • 的第主成份的方差：，。

2. 的协方差阵为，因此有：

   1. 的第个主成份的方差为，。

   2. 记，则与具有相同的散布程度。

      $$\sum_{i = 1}^p Var(y_i)=\sum_{i = 1}^p \lambda_i=tr(\Sigma)=\sum_{i = 1}^p \sigma_{ii}=\sum_{i = 1}^p Var(x_i)$$

   3. 任意两个主成份都相互独立。

定义	公式	说明
第个主成份的贡献率		表示第个主成份保留总体散布程度信息的比例.
前个主成份的累计贡献率		表示前个主成份保留总体散布程度信息的比例.
第个主成分中变量的因子负荷量
第个主成分的对于的第个分量的贡献率		表示第个主成分保留离散程度的信息的比例.
前个主成分的对于的第个分量的累计贡献率		表示前个主成分保留离散程度的信息的比例.

6.1.1 主成分与总体的相关性

记的第个行向量为，。

由于（是的特征值，是的对应的特征向量,取列向量)，因而有：

$$\sum_{i = 1}^{p}\sigma_{ji}\alpha_{ik}=\lambda_{k}\alpha_{jk} \\ \sum_{i = 1}^{p}\sigma_{ij}\alpha_{ik}=\lambda_{k}\alpha_{jk}\\ Cov(y_{k},x_{j}) = Cov\left(\sum_{i = 1}^{p}\alpha_{ik}x_{i},x_{j}\right)=\sum_{i = 1}^{p}\sigma_{ij}\alpha_{ik}=\lambda_{k}\alpha_{jk}$$

的第个主成分与的第个分量的相关系数为 :

$$\rho_{y_{k},x_{j}}=\frac{Cov(y_{k},x_{j})}{\sqrt{Var(y_{k})}\sqrt{Var(x_{j})}}=\frac{\lambda_{k}\alpha_{jk}}{\sqrt{\lambda_{k}}\sqrt{\sigma_{jj}}}=\frac{\alpha_{jk}\sqrt{\lambda_{k}}}{\sqrt{\sigma_{jj}}}$$

称为第个主成分中变量的因子负荷量。

6.1.2 主成分与X分量的复相关系数

令为与的复相关系数，，则：

$$\rho_{Y,x_{j}}^{2}=\sum_{k = 1}^{p}\rho_{y_{k},x_{j}}^{2}=\frac{1}{\sigma_{jj}}\sum_{k = 1}^{p}\lambda_{k}\alpha_{jk}^{2},\ 1\leq j\leq p$$

由，知，即有，。

则主成分与的分量的复相关系数，。

这说明主成分中含有分量的离散程度的全部信息。

事实上，有，即知 :

$$$x_{j}=\sum_{k = 1}^{p}\alpha_{jk}y_{k},1\leq j\leq p$$

6.1.3 回到例子

回答我们上述提到的问题：

Q1：第一、第二主成份代表性是否足够？

Q2：停止？还是类似地继续寻找更多的主成份？

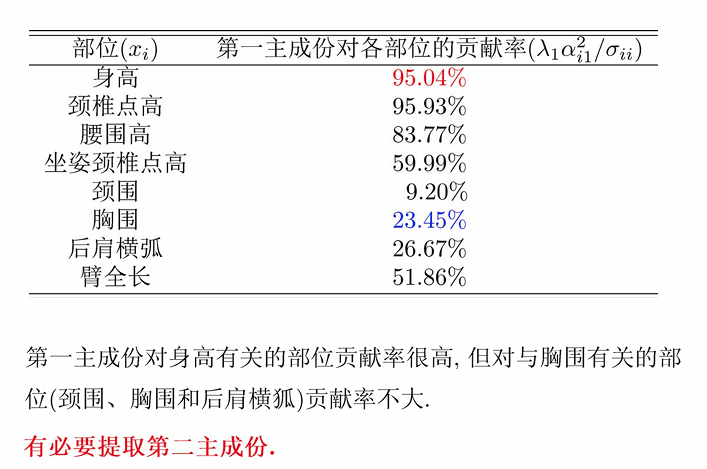
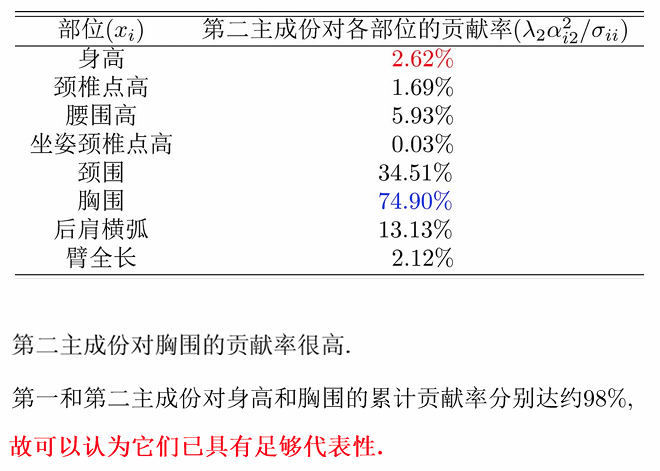
第一、二主成分对身高：

第一、二主成分对胸围：

6.2 R主成分分析:处理量纲

主成分分析主要是对随机变量的协方差矩阵进行分析，将向量投影到方差大的方向以获得重要的主成份。

Q：变量的量纲影响变量的方差，有必要消除量纲对方差的影响。

A：对变量进行标准化处理，即令:

$$X^{*}=\text{diag}(\sigma_{11}^{-1/2},\cdots,\sigma_{pp}^{-1/2})X = (\sigma_{11}^{-1/2}x_{1},\cdots,\sigma_{pp}^{-1/2}x_{p})' \\ \text{Cov}(X^{*})=\text{diag}(\sigma_{11}^{-1/2},\cdots,\sigma_{pp}^{-1/2})\Sigma\text{diag}(\sigma_{11}^{-1/2},\cdots,\sigma_{pp}^{-1/2}) = R$$

其中是的相关阵，的主成份与量纲无关。

6.2.1 R主成分分析的定义

设的特征根为$\lambda_{1}^{}\geq\cdots\geq\lambda_{p}^{}\geq0\alpha_{1}^{},\cdots,\alpha_{p}^{}T^{}=(\alpha_{1}^{},\cdots,\alpha_{p}^{*})$，

$$Y^{*}=(T^{*})'X^{*}=(T^{*})'(\sigma_{11}^{-1/2}x_{1},\cdots,\sigma_{pp}^{-1/2}x_{p})'$$

则称为的主成份。

令$Y^{}=(y_{1}^{},\cdots,y_{p}^{})’\alpha_{i}^{}=(\alpha_{1i}^{},\cdots,\alpha_{pi}^{})’$，则称:

$$y_{i}^{*}=\alpha_{i}^{*}X^{*}=\sum_{j = 1}^{p}\alpha_{ji}^{*}\sigma_{jj}^{-1/2}x_{j}$$

为的第个主成份，。

定义	公式	说明
的协方差阵	$\begin{align}\text{Cov}(Y^{})&=\Lambda^{}\&=\text{diag}(\lambda_{1}^{},\cdots,\lambda_{p}^{})\end{align}$
第个主成份的贡献率		—
前个主成份$(y_{1}^{},\cdots,y_{k}^{})$的累计贡献率		—
第个主成份中变量的因子负荷量	$\alpha_{jk}^{}\sqrt{\lambda_{k}^{}}$	$\sum_{k = 1}^{p}\lambda_{k}^{}(\alpha_{jk}^{})^{2}=1,\ 1\leq j\leq p$
前个主成份$(y_{1}^{},\cdots,y_{k}^{})Xjx_{j}$的累计贡献率	$\sum_{i = 1}^{k}\lambda_{i}^{}(\alpha_{ij}^{})^{2}$	—

6.3 样本主成分分析(基于观测数据)

假设总体，其观测样本为，则的极大似然估计为:

$$\hat{\mu}=\bar{x}=n^{-1}\sum_{i = 1}^{n}x_{i}\\ \hat{\Sigma}=S=n^{-1}\sum_{i = 1}^{n}(x_{i}-\bar{x})(x_{i}-\bar{x})'$$

样本主成份分析也就是基于样本协方差阵的主成份分析，它也等价于某个分布下的总体主成份分析。

样本主成份的定义 :(使用代替)

相关定义	说明
的特征根
与特征根对应的正则正交特征向量
为的样本主成份	令，，其中.
的第样本主成份()	记，则称.

: 和分别是的第主成份，第主成分系数和第主成份的方差的极大似然估计，。

相应地，可以得到主成份对总体的贡献率、对总体分量的因子负荷量以及总体分量的贡献率的极大似然估计。

6.3.1 经验总体下的总体主成份分析

定义随机向量，它服从离散分布，分布函数为：

$$P(X^{*}=x_{i})=\frac{1}{n}, \quad 1\leq i\leq n$$

则的分布就是样本的经验分布。

显然有：

$$\begin{align}E(X^{*})&=n^{-1}\sum_{i = 1}^{n}x_{i}=\bar{x}\\\\ Cov(X^{*})&=E[(X^{*}-E(X^{*}))(X^{*}-E(X^{*}))']\\&=n^{-1}\sum_{i = 1}^{n}(x_{i}-\bar{x})(x_{i}-\bar{x})'=S \end{align}$$

经验总体下主成份的求解 :

求的主成份	主成分	说明
(1) 求第一主成份
(2) 求第二主成份
(3) 依次求第三到第主成份		—-

因此，的主成份系数与的样本主成份系数是一致的，且:

$$Var(\hat{\alpha}_{i}'X^{*})=\hat{\lambda}_{i},\ 1\leq i\leq p$$

6.4 样本R主成分分析

基于样本相关阵的主成分分析就是样本R主成分分析。

记:

$$\hat{R} = diag(s_{11}^{-1/2},\cdots,s_{pp}^{-1/2})S \ diag(s_{11}^{-1/2},\cdots,s_{pp}^{-1/2})$$

即是样本相关阵。基于进行主成分分析即可。

此外，令:

$$x_{i}^{*} = diag(s_{11}^{-1/2},\cdots,s_{pp}^{-1/2})(x_{i}-\bar{x}), \quad 1\leq i\leq n$$

那么$x_{1}^{},\cdots,x_{n}^{}x_{1},\cdots,x_{n}\hat{R}$。

则对$x_{1}^{},\cdots,x_{n}^{}$进行主成分分析即是样本R主成分分析。

PS:

• (总体)主成分分析与R主成分分析的结论可能不一致。
• 样本主成分分析与样本R主成分分析的结论可能不一致。

6.5 主成分的统计推断

对实际数据进行的主成份分析时，事先会设定一个主成份贡献率的阈值(1 - δ)。

得到样本的主成份后，可以计算前k个样本主成份的贡献率:

如果:

$$\sum_{i = 1}^{k} \hat{\lambda}_{i} / \sum_{i = 1}^{p} \hat{\lambda}_{i} > (1 - \delta)\\$$

是否就可以认为:

$$\sum_{i = 1}^{k} \lambda_{i} / \sum_{i = 1}^{p} \lambda_{i} > (1 - \delta) ?$$

A: 需要对协差阵的特征根进行统计推断。

首先假定，则参数的似然函数为:

$$\frac{1}{|\Sigma|^{n/2}} \exp\left\{-\frac{1}{2}tr[\Sigma^{-1}(V + n(\bar{x}-\mu)(\bar{x}-\mu)')]\right\}$$

由于，即和仅与有关，其似然函数为 :

$$\begin{align}L(\lambda_{1},\cdots,\lambda_{p},\alpha_{1},\cdots,\alpha_{p})&=\frac{1}{|\Sigma|^{n/2}} \exp\left\{-\frac{1}{2}tr(\Sigma^{-1}V)\right\}\\ &=\frac{1}{|T\Lambda T'|^{n/2}} \exp\left\{-\frac{1}{2}tr(T\Lambda^{-1}T'V)\right\} \\ &= \left(\prod_{i = 1}^{p} \lambda_{i}\right)^{-n/2} \exp\left\{-\frac{1}{2}\left(\sum_{i = 1}^{p} \frac{\alpha_{i}'V\alpha_{i}}{\lambda_{i}}\right)\right\} \end{align}$$

为简单起见，再假定，即所有特征根都不等。

此时与无关。

因为由的任意性，在给定下，正交矩阵也是任意的。

事实上，考虑参数的自由度：在下

$$dim(\Lambda)=p, \quad dim(T)=p^{2}-p-\frac{p(p - 1)}{2} \\ dim(\Lambda)+dim(T)=\frac{p(p + 1)}{2}=dim(\Sigma)$$

6.5.1 Fisher信息阵与极大似然估计的渐近正态性

假设是服从密度函数为的独立样本。 记为的极大似然估计，。对数似然函数为:

$$l(\theta|X^{(n)})=\sum_{i = 1}^{n} \log \rho(x_{i},\theta)$$

则Fisher信息阵为:

$$\begin{align} I_{n}(\theta)&=V_{ar\theta}\left[\frac{\partial l(\theta|X^{(n)})}{\partial \theta}\right]\quad\text{（一般性的定义）}\\ &=-E_{\theta}\left[\frac{\partial^{2}l(\theta|X^{(n)})}{\partial \theta^{2}}\right] \\ &=-nE_{\theta}\left[\frac{\partial^{2}}{\partial \theta^{2}}\log \rho(x_{1},\theta)\right]\quad\text{（独立同分布下）}\\ &\triangleq nI(\theta) \end{align}$$

的渐近正态性(一般情形):

$$(I_{n}(\theta))^{1/2}(\hat{\theta}-\theta) \stackrel{d}{\rightarrow} N(0,I_{p}) (n\rightarrow\infty)$$

在独立同分布情形下，有 :

$$\sqrt{n}(\hat{\theta}-\theta) \stackrel{d}{\rightarrow} N(0,I^{-1}(\theta)) (n\rightarrow\infty)$$

的渐近分布

有对数似然函数:

$$l(\lambda_{1},\cdots,\lambda_{p},\alpha_{1},\cdots,\alpha_{p})=\sum_{i = 1}^{p}\left(-\frac{n}{2}\log\lambda_{i}-\frac{1}{2\lambda_{i}}\alpha_{i}'V\alpha_{i}\right)\triangleq\sum^p_{i=1}l(\lambda_i,\alpha_i)$$

因此对任意的，有:

$$\frac{\partial^{2}l(\theta|X^{(n)})}{\partial\lambda_{i}\partial\lambda_{j}} = \frac{\partial^{2}l(\lambda_{1},\cdots,\lambda_{p},\alpha_{1},\cdots,\alpha_{p})}{\partial\lambda_{i}\partial\lambda_{j}}=0$$

那么由Fisher信息阵的结构，知的极限分布是相互独立的正态分布。

的渐近方差:

由于，等价地有 :

$$V\stackrel{d}{=}\sum_{k = 1}^{n - 1}Z_{k}Z_{k}'$$

其中，是i.i.d.的正态随机向量。

因此，对，有 :

$$\alpha_{i}'V\alpha_{i}\stackrel{d}{=}\sum_{k = 1}^{n - 1}(\alpha_{i}'Z_{k})^{2}$$

由于，知是独立同分布的随机变量。因此

$$\alpha_{i}'V\alpha_{i}\stackrel{d}{=}\lambda_{i}\chi^{2}(n - 1)$$

计算的Fisher信息 :

$$\begin{align}-E_{(\lambda_{i},\alpha_{i})}\left[\frac{\partial^{2}l(\lambda_{i})}{\partial\lambda_{i}^{2}}\right]&=-E_{(\lambda_{i},\alpha_{i})}\left[\frac{n}{2\lambda_{i}^{2}}-\frac{\alpha_{i}'V\alpha_{i}}{\lambda_{i}^{3}}\right]\\ &=-\frac{n}{2\lambda_{i}^{2}}+\frac{(n - 1)\lambda_{i}}{\lambda_i^3}\\ &=\frac{n-2}{2\lambda_{i}^{2}} \end{align}$$

则的Fisher信息阵为:

$$I_{n}=diag\left(\frac{n - 2}{2\lambda_{1}^{2}},\cdots,\frac{n - 2}{2\lambda_{p}^{2}}\right)$$

由极大似然估计的渐近正态性知:

$$I_{n}^{1/2}\left(\begin{array}{c} \hat{\lambda}_{1}-\lambda_{1}\\ \vdots\\ \hat{\lambda}_{n}-\lambda_{n} \end{array}\right)\stackrel{d}{\rightarrow}N(0,I_{p})(n\rightarrow\infty) \\ n\rightarrow \infty,\quad\sqrt{n - 2}\left(\begin{array}{c} \hat{\lambda}_{1}-\lambda_{1}\\ \vdots\\ \hat{\lambda}_{n}-\lambda_{n} \end{array}\right)\stackrel{d}{\rightarrow}N(0,diag(2\lambda_{1}^{2},\cdots,2\lambda_{p}^{2}))$$

当的特征根有重根时，情况比较复杂。

由极大似然估计的渐近正态性可以构造的渐近置信区间:

$$\hat{\lambda}_{i}\left[1+\sqrt{2/(n - 2)}Z_{1-\beta/2}\right]^{-1}\leq\lambda_{i}\leq\hat{\lambda}_{i}\left[1-\sqrt{2/(n - 2)}Z_{1-\beta/2}\right]^{-1}$$

也可通过方差齐性变换，导出 :

$$\sqrt{n - 2}(\ln(\hat{\lambda}_{i}^{\sqrt{2}/2})-\ln(\lambda_{i}^{\sqrt{2}/2}))\stackrel{d}{\rightarrow}N(0,1)$$

可得的另一个置信水平为的渐近置信区间:

$$\hat{\lambda}_{i}\exp\left\{-\frac{2}{n - 2}Z_{1-\beta/2}\right\}\leq\lambda_{i}\leq\hat{\lambda}_{i}\exp\left\{\frac{2}{n - 2}Z_{1-\beta/2}\right\}$$

6.5.2 与主成分分析有关的检验问题

A.检验问题I

$$H_0:\lambda_{k + 1}+\cdots+\lambda_p\leq\gamma$$

检验统计量的构造 - 由的渐近正态性，有 :

$$\sqrt{n - 2}\left(\sum_{i = k+1}^{p}\hat{\lambda}_i-\sum_{i = k+1}^{p}\lambda_i\right)\stackrel{d}{\rightarrow}N\left(0,\sum_{i = k+1}^{p}2\lambda_i^2\right)$$

进而可得 :

$$\frac{\sqrt{n - 2}\left(\sum_{i = k+1}^{p}\hat{\lambda}_i-\sum_{i = k+1}^{p}\lambda_i\right)}{\sqrt{\sum_{i = k+1}^{p}2\hat{\lambda}_i^2}}\stackrel{d}{\rightarrow}N(0,1)$$

当:

$$\sum_{i = k+1}^{p}\hat{\lambda}_i>\gamma+\sqrt{\frac{\sum_{i = k+1}^{p}2\hat{\lambda}_i^2}{n - 2}}Z_{1-\alpha}$$

时，拒绝零假设，它犯第一类错误的概率渐近不超过。

B.检验问题II

前k个主成分的累计贡献率是否大于给定的值?

$$H_0:\frac{\sum_{i = 1}^{k}\lambda_i}{\sum_{i = 1}^{p}\lambda_i}\leq\delta$$

考虑如下的累计贡献率统计量的渐近分布 :

$$\sqrt{n - 2}\left(\frac{\sum_{i = 1}^{k}\hat{\lambda}_i}{\sum_{i = 1}^{p}\hat{\lambda}_i}-\frac{\sum_{i = 1}^{k}\lambda_i}{\sum_{i = 1}^{p}\lambda_i}\right)$$

定义如下的累计贡献率函数:

$$f(\lambda_1,\cdots,\lambda_p)=\frac{\sum_{i = 1}^{k}\lambda_i}{\sum_{i = 1}^{p}\lambda_i}$$

由Cramér定理有:

$$\sqrt{n - 2}(f(\hat{\lambda}_1,\cdots,\hat{\lambda}_p)-f(\lambda_1,\cdots,\lambda_p))\stackrel{d}{\rightarrow}N(0,\nu^2)$$

其中 :

$$\nu^2=\frac{2\left[\left(\sum_{i = k+1}^{p}\lambda_i\right)^2\left(\sum_{i = 1}^{k}\lambda_i^2\right)+\left(\sum_{i = 1}^{k}\lambda_i\right)^2\left(\sum_{i = k+1}^{p}\lambda_i^2\right)\right]}{\left(\sum_{i = 1}^{p}\lambda_i\right)^4}$$

事实上，若记,则有：

$$\frac{\partial f(\lambda)}{\partial \lambda_{i}}=\frac{I(1\leq i\leq k)}{\sum_{j = 1}^{p} \lambda_{j}}-\frac{\sum_{j = 1}^{k} \lambda_{j}}{(\sum_{j = 1}^{p} \lambda_{j})^{2}},\ 1\leq i\leq p$$

因此:

$$\begin{align} v^{2}&=\left(\frac{\partial f(\lambda)}{\partial \lambda}\right)'\text{diag}(2\lambda_{1}^{2},\cdots,2\lambda_{p}^{2})\frac{\partial f(\lambda)}{\partial \lambda}\\ &=2\sum_{i = 1}^{p} \lambda_{i}^{2}\left(\frac{I(1\leq i\leq k)}{\sum_{j = 1}^{p} \lambda_{j}}-\frac{\sum_{j = 1}^{k} \lambda_{j}}{(\sum_{j = 1}^{p} \lambda_{j})^{2}}\right)^{2} \end{align}$$

是指示函数：

将极大似然估计代入即得估计，

$$\hat{\nu}^2=\frac{2\left[\left(\sum_{i = k+1}^{p}\hat{\lambda}_i\right)^2\left(\sum_{i = 1}^{k}\hat{\lambda}_i^2\right)+\left(\sum_{i = 1}^{k}\hat{\lambda}_i\right)^2\left(\sum_{i = k+1}^{p}\hat{\lambda}_i^2\right)\right]}{\left(\sum_{i = 1}^{p}\hat{\lambda}_i\right)^4}$$

因此有:

$$\frac{\sqrt{n - 2}}{\hat v}\left(\frac{\sum_{i = 1}^{k}\hat{\lambda}_i}{\sum_{i = 1}^{p}\hat{\lambda}_i}-\frac{\sum_{i = 1}^{k}\lambda_i}{\sum_{i = 1}^{p}\lambda_i}\right)\stackrel{d}{\rightarrow}N(0,1)$$

结论：当:

$$\because\frac{\sqrt{n-2}}{\hat{\nu}} \left( \frac{\sum_{i=1}^k \hat{\lambda}_i}{\sum_{i=1}^p \hat{\lambda}_i} - \delta \right) > Z_{1-\alpha}\\ \therefore\frac{\sum_{i = 1}^{k}\hat{\lambda}_i}{\sum_{i = 1}^{p}\hat{\lambda}_i}\geq\delta+\frac{\hat{\nu}}{\sqrt{n - 2}}Z_{1-\alpha}\\ \therefore\frac{\sum_{i = 1}^{k}\lambda_i}{\sum_{i = 1}^{p}\lambda_i}>\delta$$

当标准化的统计量大于时拒绝零假设，它犯第一类错误的概率渐近不超过。

C.再次回到例子(统计检验)

样本协差阵的特征根从大到小依次为：

设定累计贡献率的阈值、显著性水平设定为

由于，我们把零假设设定为：

$$H_{0}:\frac{\sum_{i = 1}^{2}\lambda_{i}}{\sum_{i = 1}^{8}\lambda_{i}}\leq\delta = 0.85$$

即检验问题Ⅱ：前2个主成分的累计贡献率是否大于给定的值？

计算:

$$\begin{align}\hat{\nu}^{2}&=\frac{2\left[\left(\sum_{i = 3}^{8}\hat{\lambda}_{i}\right)^{2}\left(\sum_{i = 1}^{2}\hat{\lambda}_{i}^{2}\right)+\left(\sum_{i = 1}^{2}\hat{\lambda}_{i}\right)^{2}\left(\sum_{i = 3}^{8}\hat{\lambda}_{i}^{2}\right)\right]}{\left(\sum_{i = 1}^{8}\hat{\lambda}_{i}\right)^{4}}\\ &=0.0207 \end{align}$$

计算检验临界值 : 其中，

$$Z_{1-\alpha}=Z_{0.95}=1.6449\\ C_{r}=\delta+\frac{\hat{\nu}}{\sqrt{n - 2}}Z_{1-\alpha}=0.8533\\ \frac{\sum_{i = 1}^{2}\hat{\lambda}_{i}}{\sum_{i = 1}^{8}\hat{\lambda}_{i}}=0.876 > C_{r}=0.8533$$

结论：拒绝零假设，即认为，两个主成分已满足代表原总体散度的要求。

6.5.3 R主成分分析的检验

由于在R主成份分析中，样本相关阵的特征根$\hat{\lambda}_{1}^{},\cdots,\hat{\lambda}_{p}^{}\sum_{i = 1}^{p}\hat{\lambda}_{i}^{}=1\hat{\lambda}_{1}^{},\cdots,\hat{\lambda}_{p}^{*}$不再是渐近独立的。

此外，$(\lambda_{1}^{},\cdots,\lambda_{p}^{})(\alpha_{1}^{},\cdots,\alpha_{p}^{})$不再是无关的，因此有关主成份分析的渐近理论对R主成份分析不再成立。