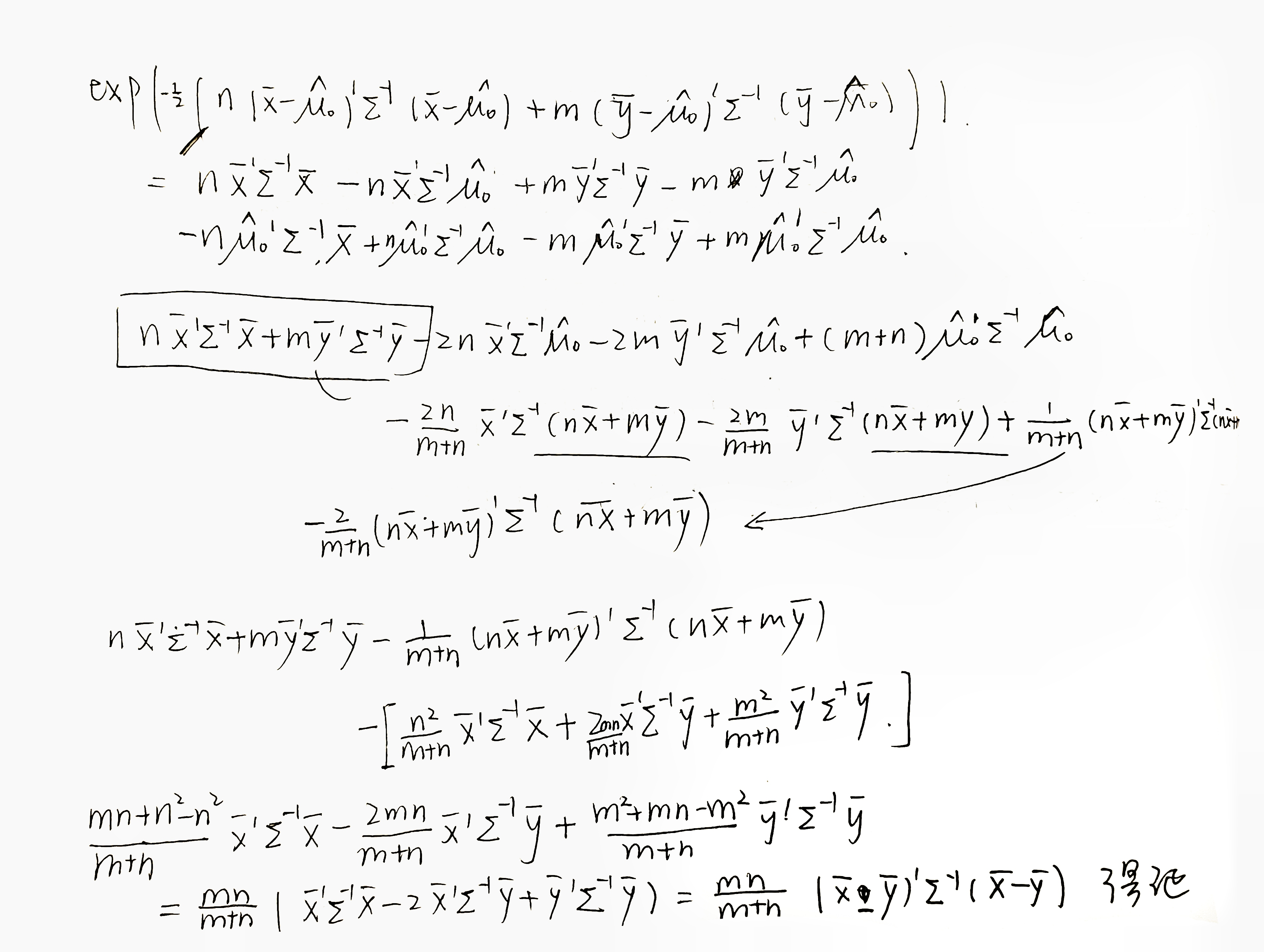多元正态统计-Ch3-多元正态分布的检验

绷不住了，上一篇写了6天？？！乐，这篇时间更久捏。

[TOC]

接续上篇，依旧讲多元正态分布，聚焦于检验部分。

主要的计算步骤：

1. 计算极大似然估计，得到极大似然估计量，比如之类。
2. 然后计算似然比：
3. 得到似然比检验统计量：/或者是其他的统计量，主要看服从何分布。

3.3 多元正态分布的检验

多元正态分布的检验问题包括：

单总体	多总体	多变量
均值检验	均值比较检验	独立性检验
协方差检验	协方差比较检验	条件独立性检验
—-	均值和协方差同时比较检验	—-

3.3.0 均值向量的改进估计

总体均值向量的极大似然估计, 定义用估计的损失函数为.

• ：取值越大，表示离的距离越来越远，损失越来越大。
• ：用估计没有损失。

实际问题中，对于均值向量的估计，希望找到一个对于所有的, 几乎处处使得风险函数=0的估计。但是实际上这样的估计通常是不存在的，因此我们退而求其次，希望找到一个估计, 使得其风险函数小于的风险，或者不比的风险大。这就是改进估计。

已知

令, 平方和损失函数定义为：

$$L(\bar x,\mu)=\sum^n_{i=1}(\bar x_i-\mu_i)'(\bar x_i-\mu_i)=(\bar x-\mu)'(\bar x-\mu)$$

一个好的估计希望平方损失越小越好，在统计决策理论中，损失函数的平均值称为风险函数。作为的估计，它在平方和损失函数下的风险函数为：

$$\begin{align} R(\bar x)&=E[L(\bar x,\mu)]=E[(\bar x-\mu)'(\bar x-\mu)]\\ &=tr\left\{E[(\bar x-\mu)'(\bar x-\mu)]\right\}\\ &=\frac{tr(\Sigma)}{n}\\ \end{align}$$

的风险函数只依赖于,与无关。

• 当p=1,2时：在平方和损失函数下，样本均值是总体均值的容许估计，改进不存在。
• 当p3时：样本均值是总体均值的不容许估计。

极大似然估计：

设是来自多元正态总体的样本，其中.

$$\begin{align*} L(\mu,\Sigma)&=\prod^n_{i=1}\frac{1}{(2\pi)^{\frac p 2}|\Sigma|^{\frac 1 2}}\exp[-\frac 1 2 (x_i-\mu)'\Sigma^{-1}(x_i-\mu)]\\ &=\frac{1}{(2\pi)^{np/2}|\Sigma|^{n/2}}\exp\left[-\frac{1}{2}\sum_{i = 1}^{n}(x_{i}-\mu)'\Sigma^{-1}(x_{i}-\mu)\right]\\ &=\frac{1}{(2\pi)^{np/2}|\Sigma|^{n/2}}\exp\left[-\frac{1}{2}\text{tr}\left(\Sigma^{-1}\left\{\sum_{i = 1}^{n}(x_{i}-\mu)(x_{i}-\mu)'\right\}\right)\right]\\ &=\frac{1}{(2\pi)^{np/2}|\Sigma|^{n/2}}\exp\left[-\frac{1}{2}\text{tr}\left(\Sigma^{-1}\{V + n(\bar{x}-\mu)(\bar{x}-\mu)'\}\right)\right] \end{align*}$$

首先给定 时，求 的极大似然估计，即求对数似然函数 的极大值点。由式(5.3)，给定 ，关于 的对数似然函数为

$$\begin{align*} \ln L(\mu,\Sigma)&=-\frac{n}{p}\ln2\pi-\frac{n}{2}\ln|\Sigma|-\frac{1}{2}\text{tr}(\Sigma^{-1}\{V + n(\bar{x}-\mu)(\bar{x}-\mu)'\})\\ &=-\frac{n}{p}\ln2\pi-\frac{n}{2}\ln|\Sigma|-\text{tr}(\Sigma^{-1}V)-\frac{n}{2}(\bar{x}-\mu)'\Sigma^{-1}(\bar{x}-\mu)\\ &\leq-\frac{n}{p}\ln2\pi-\frac{n}{2}\ln|\Sigma|-\text{tr}(\Sigma^{-1}V) \end{align*}$$

上式不等式中等号成立当且仅当 。因此，总体均值向量 的极大似然估计为样本均值向量 。由，因此，样本均值向量 是 的无偏估计。 将上式中的 用它的极大似然估计 替换，得到 的似然函数为:

$$L(\bar{x},\Sigma)=\frac{(2\pi)^{np/2}}{|\Sigma|^{n/2}}\exp\left[-\frac{1}{2}\text{tr}(\Sigma^{-1}V)\right]$$

令 ，其中 是正交矩阵， 是对角矩阵，则上式可以简化为

$$L(\bar{x},\Sigma)=\frac{1}{(2\pi)^{np/2}|V|^{n/2}}\prod_{k = 1}^{p}\left[\lambda_k^{n/2}\exp\left\{-\frac{\lambda_k}{2}\right\}\right]$$

由于 在 处取最大值，所以上式在 时取最大值，从而可知， 的极大似然估计 满足条件 。由此可见， 的极大似然估计为 。

定理5.1.2 设 为来自 元正态总体 的一组随机样本，， 为样本均值向量， 为样本离差阵，则 和 的极大似然估计分别为 和 。

3.3.1 单总体均值检验

设是来自多元正态总体的个独立样本，其中，，。 我们关心如下总体均值的检验问题：

$$H_0:\boldsymbol{\mu}=\boldsymbol{\mu}_0,\quad v.s.\quad H_1:\boldsymbol{\mu}\neq\boldsymbol{\mu}_0$$

记和分别是样本均值和样本离差阵。

似然比检验方法

假设我们有一个统计模型，参数空间为, 其中包含了所有可能的参数值。检验问题通常表述为：

$$H_0:\theta\in\Theta_0，\quad v.s.\quad H_1:\theta\in\Theta_1=\Theta\backslash\Theta_0$$

表述为参数属于一个特定的子集, 表述为参数不属于原假设所定义的子集, 即属于中除之外的所有可能值。符号 \ 表示集合的差集运算。

记样本下的似然函数为。 似然比定义为在原假设 下，似然函数的最大值与在整个参数空间 下的似然函数最大值之比。

$$\lambda=\frac{\sup_{\theta\in\Theta_0}L(\theta|X)}{\sup_{\theta\in\Theta}L(\theta|X)}$$

此处写的是上确界（所有上界中最小的一个），即使没有最大元素，但上确界仍然存在 ，这是sup与max的区别。

似然比检验统计量为 ：

$$T=-2\ln(\lambda)=-2\ln\frac{\sup_{\theta\in\Theta_0}L(\theta|X)}{\sup_{\theta\in\Theta}L(\theta|X)}$$

可以通过在零假设下的分布（零分布）构造检验的拒绝域。

(1) 已知的情形

均值参数的似然比

$$\begin{align} L(\bar{x},\Sigma)&=\frac{1}{(2\pi)^{np/2}|\Sigma|^{n/2}}\exp\left[-\frac{1}{2}\text{tr}\left(\Sigma^{-1}\{V + n(\bar{x}-\mu)(\bar{x}-\mu)'\}\right)\right]\\\\ \lambda&=\frac{\sup_{\theta\in\Theta_0}L(\theta|X)}{\sup_{\theta\in\Theta}L(\theta|X)}\\ &=\frac{\exp\left\{-\frac 1 2\text{tr}(\boldsymbol{\Sigma}^{-1}(n(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'))\right\}}{\sup_{\boldsymbol{\mu}\in\mathbb{R}^p}\left[\exp\left\{-\frac 1 2\text{tr}(\boldsymbol{\Sigma}^{-1}(n(\bar{\mathbf{x}}-\boldsymbol{\mu})(\bar{\mathbf{x}}-\boldsymbol{\mu})'))\right\}\right]} \\ &=\frac{\exp\left\{-\frac 1 2n(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'\boldsymbol{\Sigma}^{-1}(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)\right\}}{\sup_{\boldsymbol{\mu}\in\mathbb{R}^p}\left[\exp\left\{-\frac 1 2n(\bar{\mathbf{x}}-\boldsymbol{\mu})'\boldsymbol{\Sigma}^{-1}(\bar{\mathbf{x}}-\boldsymbol{\mu})\right\}\right]}\\ &=\frac{\exp\left\{-\frac 1 2 n(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'\boldsymbol{\Sigma}^{-1}(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)\right\}}{\exp\left\{-\frac 1 2 n(\bar{\mathbf{x}}-\boldsymbol{\hat\mu})'\boldsymbol{\Sigma}^{-1}(\bar{\mathbf{x}}-\boldsymbol{\hat\mu})\right\}},\quad\hat\mu=\bar x\\ & =\exp\left\{-\frac 1 2n(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'\boldsymbol{\Sigma}^{-1}(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)\right\} \end{align}$$

因此似然比检验统计量为

$$T = - 2\ln(\lambda)=n(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'\boldsymbol{\Sigma}^{-1}(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)$$

故当时拒绝零假设，其犯第一类错误的概率为。

(2) 未知的情形

记 参数的似然比为 ():

$$\begin{align} \lambda&=\frac{\sup_{\boldsymbol{\Sigma}}\left[|\boldsymbol{\Sigma}|^{-n/2}\exp\left\{-\frac 1 2\text{tr}(\boldsymbol{\Sigma}^{-1}(V + n(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'))\right\}\right]}{\sup_{\{\boldsymbol{\mu},\boldsymbol{\Sigma}\}}\left[|\boldsymbol{\Sigma}|^{-n/2}\exp\left\{-\frac 1 2\text{tr}(\boldsymbol{\Sigma}^{-1}(V + n(\bar{\mathbf{x}}-\boldsymbol{\mu})(\bar{\mathbf{x}}-\boldsymbol{\mu})'))\right\}\right]}\\ &=\frac{\sup_{\boldsymbol{\Sigma}}\left[|\boldsymbol{\Sigma}|^{-n/2}\exp\left\{-\frac 1 2\text{tr}(\boldsymbol{\Sigma}^{-1}V_0)\right\}\right]}{\sup_{\{\boldsymbol{\mu},\boldsymbol{\Sigma}\}}\left[|\boldsymbol{\Sigma}|^{-n/2}\exp\left\{-\frac 1 2\text{tr}(\boldsymbol{\Sigma}^{-1}(V + n(\bar{\mathbf{x}}-\boldsymbol{\mu})(\bar{\mathbf{x}}-\boldsymbol{\mu})'))\right\}\right]} \\ &=\frac{|\boldsymbol{\hat\Sigma_0}|^{-n/2}\exp\left\{-\frac 1 2\text{tr}(\boldsymbol{\hat\Sigma_0}^{-1}V_0)\right\}}{|\boldsymbol{\hat\Sigma}|^{-n/2}\exp\left\{-\frac 1 2\text{tr}(\boldsymbol{\hat\Sigma}^{-1}(V + n(\bar{\mathbf{x}}-\boldsymbol{\hat\mu})(\bar{\mathbf{x}}-\boldsymbol{\hat\mu})'))\right\}} \\ \end{align}$$

其中是原假设为真时：时的极大似然估计。

$$\hat\Sigma_0=\frac1n\sum^n_{i=1}(x_i-\mu_0)(x_i-\mu_0)'$$

分母中的是当时，的极大似然估计。

$$\hat \mu=\bar x\\ \hat\Sigma=\frac 1 n \sum^n_{i=1}(x_i-\bar x) (x_i-\bar x)'=\frac V n$$

继续计算, 分母后面的exp因为所以等于0，;且有：

$$\begin{align} \lambda&=\frac{|\frac{V_0}n|^{-n/2}e^{-\frac {np} 2}}{\left|\frac V n\right|^{-n/2}},\quad e^{-\frac {np} 2}常数项忽略\\ &=\frac{\left|V_0\right|^{-n/2}}{\left|V\right|^{-n/2}}\\ &=\left(\frac{\left|V\right| + n(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'}{\left|V\right|}\right)^{-n/2} \\ &=\left|I_p + nV^{-1/2}(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'V^{-1/2}\right|^{-n/2}\\ &=(1 + n(\bar{\mathbf{x}}-\boldsymbol{\mu}_0)'V^{-1}(\bar{\mathbf{x}}-\boldsymbol{\mu}_0))^{-n/2} \end{align}$$

利用似然比原理，在较小时拒绝原假设, 从而认为备择假设成立. 当原假设成立时，由, 所以通常取：

$$T^{2}=n(n - 1)(\bar{x}-\mu_{0})'V^{-1}(\bar{x}-\mu_{0})=n(\bar{x}-\mu_{0})'S^{-1}(\bar{x}-\mu_{0})$$

为检验统计量。并在较大时拒绝原假设, 从而认为备择假设成立。

根据Hotelling 分布的性质有:

$$T^{2} \stackrel{d}{\rightarrow} T_{p}^{2}(n - 1)\\ \frac{n - p}{(n - 1)p}T^{2} \stackrel{d}{\rightarrow} F(p, n - p)$$

则当时拒绝零假设，其犯第一类错误的概率为。

检验的p值为：

$$p_v=Pr(F_{p,n-p}\ge\frac{n-p}{(n-1)p}T^2)$$

栗子(检验单总体、两总体均值)

(1): 在正态假设下，哥特式教堂的长度和中殿长度是否与罗马式教堂具有相同的均值？

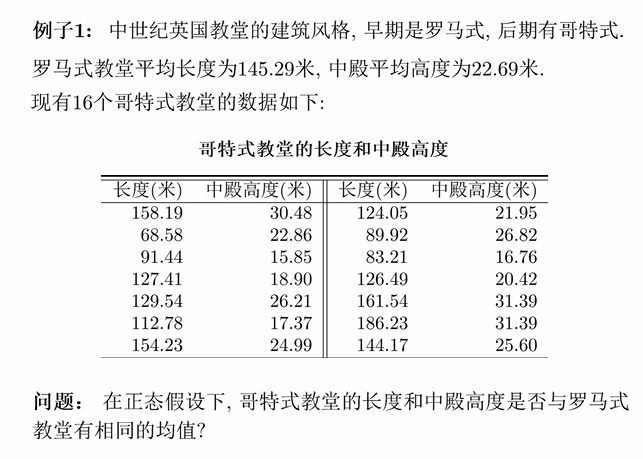
计算哥特式教堂数据的:

$$\bar x=\begin{pmatrix}121.12\\22.84\end{pmatrix},V=\begin{pmatrix}19466.70& 2257.90\\2257.90& 469.56\end{pmatrix}$$

n=16,p=2, , 未知。

$$T^2=n(n-1)(\bar X-\mu_0)'V^{-1}(\bar X-\mu_0)=17.283\\$$

设定显著性水平为, 计算检验的p值：

$$\begin{align} p_v&=Pr(F_{p,n-p}\ge\frac{n-p}{(n-1)p}T^2)\\ &=Pr(F(2,14)\ge8.0654)\\ &=0.0047\\ &<0.05 \end{align}$$

结论：故拒绝零假设，, 认为哥特式教堂和罗马式教堂没有相同的长度和中殿高度。

(2): 哥特式教堂的长度与罗马式教堂长度是否具有相同的均值？

这实际上是一个单总体正态分布检测。哥特式教堂的样本协方差阵:

$$S=\frac{V}{n-1}=\begin{pmatrix}19466.70/15& 2257.90/15\\2257.90/15& 469.56/15\end{pmatrix}=\begin{pmatrix}12977.78& 150.53\\150.53& 31.3\end{pmatrix}=\begin{pmatrix}s_{11}&s_{12}\\s_{21}&s_{22}\end{pmatrix}$$

t-检验与检验的p值：

$$t_1=\sqrt n \frac{\bar X_1-145.29}{\sqrt{s_{11}}} =4\frac{121.12-145.29}{\sqrt{1297.78}} =-2.648\\\\ p=Pr\left\{|t(15)|\ge|t_1|\right\}=2Pr(t(15)\le -2.648)=0.017\le0.05$$

总结：因此认为哥特式教堂的长度与罗马式教堂长度没有相同均值。

(3): 哥特式教堂的中殿高度与罗马式教堂的中殿高度是否具有相同的均值？

$$t_2=\sqrt n\frac{\bar X_2-22.69}{\sqrt{s_{22}}}=4\times\frac{22.84-22.69}{\sqrt{31.3}}=0.107\\\\ p=Pr\left\{|t(15)|\ge|t_2|\right\}=2Pr(t(15)\ge 0.107)=0.916\gt 0.05$$

总结：因此认为哥特式教堂的中殿高度与罗马式教堂的中殿高度具有相同的均值.

两种教堂长度和中殿高度的比较问题（例1续）

如果设定 。 考虑如下的协方差阵 未知时的均值检验问题：

$$H_0:\mu = \mu_0^*，\quad v.s.\quad H_1:\mu\neq\mu_0^*$$

此时Hotelling 检验统计量、计算的p值为 ：

$$T^2=n(n - 1)(\bar{X}-\mu_0^*)'V^{-1}(\bar{X}-\mu_0^*) = 11.507\\\\ p=P\left\{F(p,n - p)\geq\frac{n - p}{(n - 1)p}T^2\right\} =P\left\{F(2,14)\geq5.370\right\}=0.019$$

结论：拒绝零假设。

1’) 哥特式教堂的长度与罗马式教堂长度是否有相同均值的t - 检验、p值：

$$t_1^*=\sqrt{n}\cdot\frac{\bar{X}_1 - 131}{\sqrt{S_{11}^*}}=\sqrt{16}\cdot\frac{121.12 - 131}{\sqrt{1297.78}}=-1.097\\\\ p = P_r\{|t(15)|\geq|t_1^*|\}=2P_r\{t(15)\leq - 1.097\}=0.290>0.05$$

结论：因此认为哥特式教堂的长度与罗马式教堂长度有相同均值。

2’) 哥特式教堂的中殿高度与罗马式教堂的中殿高度是否有相同均值的t - 检验、p值：

$$t_2^*=\sqrt{n}\cdot\frac{\bar{X}_2 - 21}{\sqrt{S_{22}^*}}=\sqrt{16}\cdot\frac{22.84 - 21}{\sqrt{31.30}}=1.315\\\\ p = P_r\{|t(15)|\geq|t_2^*|\}=2P_r\{t(15)\geq1.315\}=0.208>0.05$$

结论：因此认为哥特式教堂的中殿高度与罗马式教堂的中殿高度有相同的均值。

3.3.2 两个多元总体均值比较的检验

记 和 分别为来自总体 和 的独立样本，，，。

两个总体均值是否相等的检验问题为:

$$H_0:\mu_1 = \mu_2，\quad v.s.\quad H_1:\mu_1\neq\mu_2$$

注意：此时两个总体的协方差阵相等。 记 和 分别为总体 和 的样本均值。

(1) 已知的情形

的似然函数为(去掉常数项):

$$L(\mu_1,\mu_2)=\exp\left\{-\frac{1}{2}[m(\bar{x}-\mu_1)'\Sigma^{-1}(\bar{x}-\mu_1)+n(\bar{y}-\mu_2)'\Sigma^{-1}(\bar{y}-\mu_2)]\right\}\\ \hat{\mu}_0=\frac{m\bar{x}+n\bar{y}}{m + n}=\frac{\sum_{i = 1}^{m}x_i+\sum_{j = 1}^{n}y_j}{m + n}$$

当 时， 的极大似然估计是 。

检验问题的似然比为:

$$\begin{align} \lambda&=\frac{\sup_{\mu}L(\mu,\mu)}{\sup_{\{\mu_1,\mu_2\}}L(\mu_1,\mu_2)}\\ &=\exp\left\{-\frac{1}{2}[m(\bar{x}-\hat{\mu}_0)'\Sigma^{-1}(\bar{x}-\hat{\mu}_0)+n(\bar{y}-\hat{\mu}_0)'\Sigma^{-1}(\bar{y}-\hat{\mu}_0)]\right\}\\ &=\exp\left\{-\frac{1}{2}\left[\frac{mn}{m + n}(\bar{x}-\bar{y})'\Sigma^{-1}(\bar{x}-\bar{y})\right]\right\} \end{align}$$

$$m(\bar{x}-\hat{\mu}_0)'\Sigma^{-1}(\bar{x}-\hat{\mu}_0)+n(\bar{y}-\hat{\mu}_0)'\Sigma^{-1}(\bar{y}-\hat{\mu}_0)=\frac{mn}{m + n}(\bar{x}-\bar{y})'\Sigma^{-1}(\bar{x}-\bar{y})$$

则检验比检验统计量为:

$$T=-2\log(\lambda)=\frac{mn}{m + n}(\bar{x}-\bar{y})'\Sigma^{-1}(\bar{x}-\bar{y})\vert_{H_0}\stackrel{d}{\sim}\chi^2(p)$$

当 时拒绝零假设，其犯第一类错误的概率为 。

(2) 未知的情形

记和分别为总体和的样本离差阵，。

的似然函数为:

$$L(\mu_1,\mu_2,\Sigma)=\frac{1}{\vert\Sigma\vert^{\frac{(m + n)}2}} \exp\left\{-\frac{1}{2}\text{tr}[\Sigma^{-1}(V + m(\bar{x}-\mu_1)(\bar{x}-\mu_1)' + n(\bar{y}-\mu_2)(\bar{y}-\mu_2)')]\right\}$$

当时，和的极大似然估计分别为：，的极大似然估计为.在原假设成立时()，的极大似然估计为. 在原假设成立时，将似然函数中的均值向量, 从而得到原假设成立时的的似然函数为：

$$\begin{align} L(\Sigma)&=\frac{1}{\vert\Sigma\vert^{\frac{(m + n)}2}} \exp\left\{-\frac{1}{2}\text{tr}[\Sigma^{-1}(V_1+V_2 + m(\bar{x}-\hat\mu_0)(\bar{x}-\hat\mu_0)' + n(\bar{y}-\hat\mu_0)(\bar{y}-\hat\mu_0)')]\right\}\\ \hat \Sigma_0&=\frac{V_1+V_2 + m(\bar{x}-\hat\mu_0)(\bar{x}-\hat\mu_0)'+ n(\bar{y}-\hat\mu_0)(\bar{y}-\hat\mu_0)'}{m+n}\\ \hat \Sigma_0&=\frac{V_1+V_2 + \frac{mn}{m + n}(\bar{x}-\bar{y})(\bar{x}-\bar{y})'}{m+n} \end{align}$$

因为, 所以有

检验问题的似然比为:

$$\begin{align} \lambda&=\frac{\sup_{\{\mu,\Sigma\}}L(\mu,\mu,\Sigma)}{\sup_{\{\mu_1,\mu_2,\Sigma\}}L(\mu_1,\mu_2,\Sigma)}\\ &=\left(\frac{\vert V_1+V_2 + \frac{mn}{(m + n)}(\bar{x}-\bar{y})(\bar{x}-\bar{y})'\vert}{\vert V_1+V_2\vert}\right)^{-(m + n)/2}\\ &=\vert I_p+\frac{mn}{m+n}(V_1+V_2)^{-\frac 1 2}(\bar{x}-\bar{y})(\bar{x}-\bar{y})'(V_1+V_2)^{-\frac 1 2}\vert^{-(m + n)/2}\\ &=\left(1+\frac{mn}{m + n}(\bar{x}-\bar{y})'(V_1+V_2)^{-1}(\bar{x}-\bar{y})\right)^{-(m + n)/2} \end{align}$$

令 :

$$T^2=\frac{mn(m + n - 2)}{m + n}(\bar{x}-\bar{y})'(V_1+V_2)^{-1}(\bar{x}-\bar{y})\\\\ T^2\vert_{H_0}\stackrel{d}{\sim}T^2_p(m + n - 2)$$

取为检验统计量，在原假设为真()时，, 且在较大时拒绝原假设, 从而认为备择假设成立(). 再根据Hotelling 分布的性质：

$$\frac{1}{(m + n - 2)}T^2_p(n+m-2)\overset{d}{=}\frac{\chi^2_p}{\chi^2_{m + n - p - 1}}\\ \frac{(m + n - p - 1)}{(m + n - 2)p}T^2\overset{d}{\sim}F(p,m + n - p - 1)\\ p_v=Pr\left( F_{1-\alpha}(p,m + n - p - 1)\ge\frac{(m + n - p - 1)}{(m + n - 2)p}T^2\right)$$

因此，当 时拒绝零假设， 其犯第一类错误的概率为 。

MLE小结

似然比检验统计量由似然函数在极大似然估计下的似然函数值决定。

相同协方差阵下正态总体均值和协方差阵的极大似然估计(MLE)：

均值	协方差阵
单总体：均值的极大似然估计为样本均值;	计算在给定均值极大似然估计下协方差阵的似然函数:
多总体：各总体均值无约束的极大似然估计为各自的样本均值;
多总体：在各总体均值相等的约束条件下，均值的极大似然估计为将所有样本看成是来自同一总体时的样本均值;	其中是仅与数据有关的正定矩阵，则协方差矩阵的极大似然估计。

3.3.3 多元Behrens - Fisher问题

记 和 分别为来自总体 和 的独立样本，，，。

Behrens - Fisher问题：即在 时，如下的检验问题：

$$H_0:\mu_1 = \mu_2，\quad v.s.\quad H_1:\mu_1\neq\mu_2$$

(1) 的情形

令 ，易知 是来自总体 的独立样本， 其中，，，，。 因此，对 做 未知下的如下检验即可

$$H_0:\mu = 0,\quad v.s.\quad H_1:\mu\neq 0$$

即单总体协方差阵未知时均值是否为0的检验。

因为X,Y同是n维“向量”，所以可将作为一个单独的多元正态总体，. 所以检验就是检验.

(2) 的情形

检验统计量为：

$$T^2 = (\bar{x}-\bar{y})'S^{-1}(\bar{x}-\bar{y})$$

其中，，，分别是，的样本协方差阵。

2.1) 有限样本下的近似分布

在零假设下，近似服从Hotelling分布:

$$f=\frac{ \left[(\bar{x}-\bar{y})'S^{-1}(\bar{x}-\bar{y})\right]^2 }{ \frac{\left[(\bar{x}-\bar{y})'S^{-1}S_XS^{-1}(\bar{x}-\bar{y})\right]^2}{m^2(m - 1)} + \frac{\left[(\bar{x}-\bar{y})'S^{-1}S_YS^{-1}(\bar{x}-\bar{y})\right]^2}{n^2(n - 1)} }$$

相应检验的值为:

$$p = P\left\{F(p,f - p + 1)\geq\frac{f - p + 1}{fp}T^2\right\}$$

2.2) 渐近分布 (总体不服从正态分布)

或者是，没有证据表明总体服从正态分布。因此，我们将其渐渐近为正态分布来计算。

假设，，， 则在零假设下有:

$$T^2\stackrel{d}{\to}\chi^2(p)$$

则当时拒绝零假设，其犯第一类错误的概率近似为。

也可以用分布的一阶校正来近似的分布。

Q: 分布的一阶校正是什么？

A: 一阶校正（First-Order Correction）在统计学中指的是对某一统计量的分布进行调整，以提高其与理论分布（如卡方分布）的拟合度，尤其是在样本量较小或其他条件不完全满足时。这种校正旨在减少近似分布与实际分布之间的偏差，从而提高假设检验的准确性和可靠性。通过一阶校正，统计量在有限样本下的分布更接近于分布，从而提高了假设检验的准确性。

Bartlett校正（Bartlett Correction）:

Bartlett校正是最常见的一阶校正方法之一，主要应用于似然比检验（Likelihood Ratio Test, LRT）中。其基本思想是通过引入一个校正因子，调整似然比统计量，使其在有限样本下的均值更接近卡方分布的均值。

定义：设为未校正的似然比统计量，其期望值在原假设下通常为自由度的数目，但在有限样本下可能偏离。Bartlett校正通过引入一个校正因子，定义校正后的统计量为：

$$T_{\text{校正}} = c \cdot T$$

使得的期望值更接近于分布的自由度。

Hotelling的检验中的一阶校正:

当样本量不等时，检验统计量的分布在有限样本下并不完全符合卡方分布，因此需要进行一阶校正以提高检验的准确性。

具体步骤：

1. 计算未校正的统计量：

   $$T^2 = (\bar{x} - \bar{y})' S^{-1} (\bar{x} - \bar{y})$$

   其中，，和分别是两个样本的离差平方和矩阵。

2. 计算Bartlett校正因子：

   校正因子的具体计算公式依赖于具体的检验方法和样本数据。在Hotelling的检验中，通常基于样本量、变量数目和样本协方差矩阵的特性来确定。

3. 计算校正后的统计量：

   $$T_{\text{校正}} = c \cdot T^2$$

4. 确定检验的p值：

   使用校正后的统计量，根据卡方分布计算p值：

   $$p = P\left\{ \chi^2(p) \geq T_{\text{校正}} \right\}$$

另外，可以尝试似然比统计量及其渐近分布。

Wilks定理： (Wilks定理 为这些似然比检验提供了理论基础，说明在原假设成立时，检验统计量的渐近分布为卡方分布。)

在正则条件下，对检验问题:

$$H_0:\theta\in\Theta_0,\quad v.s. \quad H_1:\theta\in\Theta_1=\Theta\backslash\Theta_0$$

似然比检验统计量:

$$T = - 2\log(\lambda)=- 2\log\frac{\sup_{\theta\in\Theta_0}L(\theta|X)}{\sup_{\theta\in\Theta}L(\theta|X)}$$

在零假设下有极限分布:

$$T\vert_{H_0}\stackrel{d}{\to}\chi^2(p)$$

其中 。

例：Behrens - Fisher检验问题

。 设有一组数据，经处理后有：

$$\bar{x}=\begin{pmatrix}9.82\\15.06\end{pmatrix},\quad\bar{y}=\begin{pmatrix}13.05\\22.57\end{pmatrix}\\ S_x=\begin{pmatrix}120.000&-16.304\\-16.304&17.792\end{pmatrix},\quad S_y=\begin{pmatrix}81.796&32.098\\32.098&53.801\end{pmatrix}$$

其中，，，。 没有证据认为，因而这是Behrens - Fisher检验问题。采用近似Hotelling 检验方法。 经计算得:

$$\bar x-\bar y=\begin{pmatrix}-3.23\\-7.51\end{pmatrix}\\ S=\frac{S_x}{m}+\frac{S_y}{n}=\begin{pmatrix}7.5&-1.019\\-1.019&1.112\end{pmatrix}+\begin{pmatrix}7.436&2.918\\2.918&4.891\end{pmatrix}=\begin{pmatrix}14.936&1.899\\1.899&6.003\end{pmatrix}\\ T^2 = (\bar{x}-\bar{y})'S^{-1}(\bar{x}-\bar{y})=9.4447$$

代入公式得自由度。

import numpy as np

S_x = np.array([[ 120, -16.304],[-16.304,  17.792]] )
S_y = np.array([[81.796,32.098],[32.098,53.801]])
x_y= np.array([[-3.23], [-7.51]])
S_itv= np.array([[ 0.06975803, -0.02206738],[-0.02206738,0.17356421]] )

ans_1 = np.dot(np.dot(x_y.T,S_itv),x_y)**2
ans_2 = np.dot(np.dot(np.dot(np.dot(x_y.T,S_itv),S_x),S_itv),x_y)**2/(16*16*15)
ans_3 = np.dot(np.dot(np.dot(np.dot(x_y.T,S_itv),S_y),S_itv),x_y)**2/(11*11*10)

f = ans_1/(ans_2+ans_3)

print(ans_1) # [[89.23120903]]
print(ans_2) # [[0.16334961]]
print(ans_3) # [[6.2108612]]
print(f) # [[13.99878537]]约等于14

因此检验的值为:

$$\begin{align} 0.025&< P\left\{F(p,f - p + 1)\geq\frac{f - p + 1}{fp}T^2\right\}\\ &= P\left\{F(2,13)\geq\frac{13}{28}T^2\right\} \\ &<0.05 \end{align}$$

结论：拒绝零假设。

3.3.4 多元方差分析

设有 个相互独立的总体 ，，。

是来自总体 的样本，。记 ，。

考虑检验问题：

$$H_0:\mu_1=\cdots=\mu_k,\quad v.s.\quad H_1:\mu_1,\cdots,\mu_k 不全相等$$

我们要检验的是 k 个多元正态总体均值向量是否都相同。

似然函数为 :

$$L(\mu_1,\cdots,\mu_k,\Sigma)=\vert\Sigma\vert^{-n/2}\exp\left\{-\frac{1}{2}\text{tr}\left(\Sigma^{-1}\left[\sum_{i = 1}^{k}V_i+\sum_{i = 1}^{k}n_i(\bar{x}_i-\mu_i)(\bar{x}_i-\mu_i)'\right]\right)\right\}$$

其中， 和 分别是第 个总体的样本均值和样本离差阵，。 记 为全部样本下的样本均值。

$$\bar x=\frac 1 n\sum_{i = 1}^{k}n_i\bar{x}_i\\ \bar{x}_i = \frac{1}{n_i}\sum_{j=1}^{n_i} x_{ij}\\ V_i = \sum_{j=1}^{n_i} (x_{ij} - \bar{x}_i)(x_{ij} - \bar{x}_i)'$$

似然函数的推导:

给定参数 的前提下，各个样本来自互相独立的多元正态总体，因此联合似然函数可表示为：

$$L(\mu_1,\ldots,\mu_k,\Sigma) = \prod_{i=1}^k \prod_{j=1}^{n_i} f(x_{ij}|\mu_i,\Sigma)$$

其中多元正态密度函数为：

$$f(x_{ij}|\mu_i,\Sigma)= \frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}\exp\left(-\frac{1}{2}(x_{ij}-\mu_i)'\Sigma^{-1}(x_{ij}-\mu_i)\right)$$

将所有样本合并，取对数似然函数 ，再略去与参数无关的常数项并经过一定的矩阵代数运算与整理（使用迹的运算属性），最终得到

$$L(\mu_1,\cdots,\mu_k,\Sigma)= | \Sigma |^{-n/2}\exp\left\{-\frac{1}{2}\text{tr}\left[\Sigma^{-1}\left(\sum_{i=1}^k V_i + \sum_{i=1}^k n_i(\bar{x}_i - \mu_i)(\bar{x}_i - \mu_i)'\right)\right]\right\}$$

在这里，我们可以看到似然函数中分为两部分：

1. ：反映了所有组内部的变异信息（各组样本点围绕各自组均值的变异）。
2. ：反映了样本组均值与总体均值之间的偏差。

(1) 已知的情形

检验问题的似然比为:

$$\begin{align} \lambda&=\frac{\sup_{\mu}L(\mu,\cdots,\mu)}{\sup_{\{\mu_1,\cdots,\mu_k\}}L(\mu_1,\cdots,\mu_k)} \\ &=\frac{ | \Sigma |^{-n/2}\exp\left\{-\frac{1}{2}\text{tr}\left[\Sigma^{-1}\left(\sum_{i=1}^k V_i + \sum_{i=1}^k n_i(\bar{x}_i - \mu)(\bar{x}_i - \mu)'\right)\right]\right\}}{ | \Sigma |^{-n/2}\exp\left\{-\frac{1}{2}\text{tr}\left[\Sigma^{-1}\sum_{i=1}^k V_i\right] \right\}}\\ &=\exp\left\{-\frac{1}{2}\text{tr}\left(\Sigma^{-1}\left[\sum_{i = 1}^{k}n_i(\bar{x}_i-\bar{x})(\bar{x}_i-\bar{x})'\right]\right)\right\} \end{align}$$

为组间离差阵 (Sum of Squares Between)。

则似然比检验统计量为 :

$$\begin{align} T&=-2\log(\lambda)=\text{tr}\left[\Sigma^{-1}(\text{SSB})\right] \\ &=\sum_{i = 1}^{k}\text{tr}\left(n_i\Sigma^{-1}(\bar{x}_i-\bar{x})(\bar{x}_i-\bar{x})'\right) \\ &=\sum_{i = 1}^{k}n_i(\bar{x}_i-\bar{x})'\Sigma^{-1}(\bar{x}_i-\bar{x}) \end{align}$$

在原假设的大样本情形下，T渐近服从分布。

$$\begin{align} \text{SSB}\stackrel{d}{\sim}W_p(k - 1,\Sigma)& \Rightarrow \Sigma^{-1/2}(\text{SSB})\Sigma^{-1/2}\stackrel{d}{\sim}W_p(k - 1,I_p) \\ &\Rightarrow \text{tr}(\Sigma^{-1/2}(\text{SSB})\Sigma^{-1/2})\stackrel{d}{\sim}\chi^2((k - 1)p) \\ &\Rightarrow \text{tr}[\Sigma^{-1}(\text{SSB})]\stackrel{d}{\sim}\chi^2((k - 1)p)\\ &\Rightarrow T\stackrel{d}{\sim}\chi^2((k - 1)p \end{align}$$

若观测到的检验统计量 ，则在显著性水平 下拒绝原假设 ，否则不拒绝。

(2) 未知的情形

SSW为组内离差阵 (Sum of Squares Within)，SST为总离差阵 (Total Sum of Squares)，记为:

$$\text{SSW}=\sum_{i = 1}^{k}V_i=\sum_{i = 1}^{k}\sum_{j = 1}^{n_i}(x_{ij}-\bar{x}_i)(x_{ij}-\bar{x}_i)'\\ V_i\sim W_p(n_{i}-1,\Sigma)\ i.i.d.\\ SSW\sim W_p(n-k,\Sigma)\\\\ \begin{align} \text{SST}&=\sum_{i = 1}^{k}V_i+\sum_{i = 1}^{k}n_i(\bar{x}_i-\bar{x})(\bar{x}_i-\bar{x})' \\ &=\text{SSW}+\text{SSB} \\ &=\sum_{i = 1}^{k}\sum_{j = 1}^{n_i}(x_{ij}-\bar{x})(x_{ij}-\bar{x})' \end{align}$$

由前面的分析有: 。当原假设成立时，，且SSW和SSB相互独立。则检验的似然比为:

$$\lambda=\frac{\sup_{\{\mu,\Sigma\}}L(\mu,\cdots,\mu,\Sigma)}{\sup_{\{\mu_1,\cdots,\mu_k,\Sigma\}}L(\mu_1,\cdots,\mu_k,\Sigma)} =\left(\frac{\vert\text{SSW}\vert}{\vert\text{SSW}+\text{SSB}\vert}\right)^{\frac n 2}$$

利用似然比原理，在较小时拒绝原假设，从而认为备择假设成立，即。当原假设成立时，SSW和SSB相互独立。由Wilks分布定义得：

$$\Lambda=\frac{\vert SSW\vert}{\vert SSW+SSB\vert}\sim\Lambda(p,n-k,k-1)$$

因此，当 时拒绝零假设。 也可以用似然比检验统计量的渐近分布，即:

$$- 2\log(\lambda)=- n\log(\Lambda)\stackrel{d}{\to}\chi^2((k - 1)p)$$

定理3.1 在原假设成立时，有如下结论成立：

$$\text{SST}\stackrel{d}{\sim}W_p(n - 1,\Sigma)\\ \text{SSW}\stackrel{d}{\sim}W_p(n - k,\Sigma)\\ \text{SSB}\stackrel{d}{\sim}W_p(k - 1,\Sigma)$$

且与相互独立。

证明：

记 ，其中 ， 记 为 的全1矩阵，并令

$$\begin{align} C &= I_n - J_n/n\\ C_1&=\begin{pmatrix} I_{n_1}-J_{n_1}/n_1&0&\cdots&0\\ 0&I_{n_2}-J_{n_2}/n_2&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&0&I_{n_k}-J_{n_k}/n_k \end{pmatrix}\\ C_2 &= C - C_1 \end{align}$$

不难推知有 :

$$\text{SST}=XCX'\\ \text{SSW}=XC_1X'\\ \text{SSB}=XC_2X'$$

又知 和 都是幂等阵，且:

$$\text{rank}(C)=\text{tr}(C)=n - 1,\quad \text{rank}(C_1)=\text{tr}(C_1)=n - k, \\ \text{SST}-\text{SSW}=\text{SSB}>0$$

在零假设下，它们的分布与共同的 无关， 因此可设 是服从 的矩阵正态分布， 由 Wishart 分布二次型的性质得证定理。

当总体数，或样本维数时，可以转化为分布。

p/k	检验统计量
p=1
k=2
p=2
k=3

例：多元方差分析

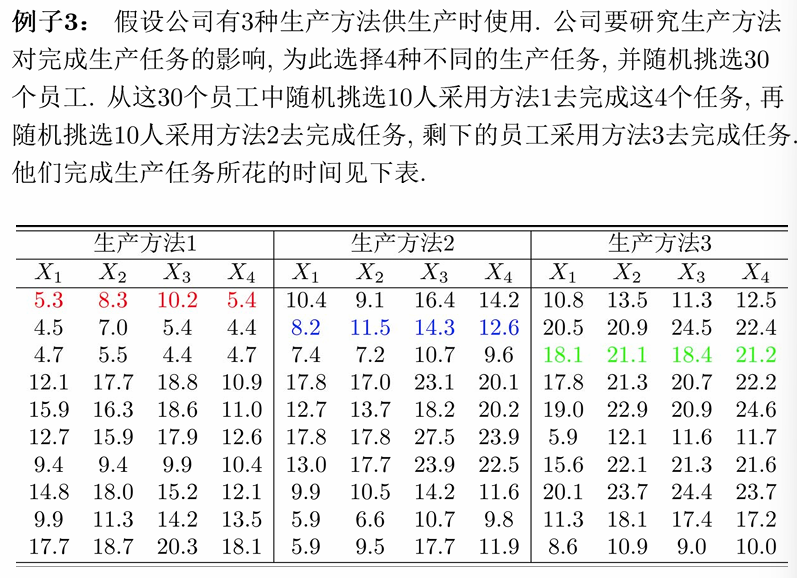
检验问题：这3种生产方法对完成任务是否有差异？

本例中，总体个数 ，样本维数 。

3个总体的样本量，总样本量。

假设3个总体均为正态，且协方差阵相等但未知。 采用Wilks检验。

计算3个总体的样本离差阵为

$$V_1=\begin{pmatrix} 204.74 & 203.56 & 224.07 & 165.01\\ 203.56 & 228.71 & 245.87 & 159.91\\ 224.07 & 245.87 & 295.35 & 189.77\\ 165.01 & 159.91 & 189.77 & 170.65 \end{pmatrix} \\ V_2=\begin{pmatrix} 173.66 & 150.15 & 191.63 & 192.39\\ 150.15 & 163.34 & 202.17 & 198.70\\ 191.63 & 202.17 & 287.38 & 259.35\\ 192.39 & 198.70 & 259.35 & 268.18 \end{pmatrix}\\ V_3=\begin{pmatrix} 244.64 & 205.11 & 236.86 & 239.73\\ 205.11 & 203.34 & 225.30 & 230.08\\ 236.86 & 225.30 & 277.15 & 258.73\\ 239.73 & 230.08 & 258.73 & 265.79 \end{pmatrix}\\$$

计算组内离差阵、组间离差阵为:

$$\text{SSW}=V_1 + V_2+V_3=\begin{pmatrix} 623.04 & 558.82 & 652.56 & 597.13\\ 558.82 & 595.40 & 673.34 & 588.69\\ 652.56 & 673.34 & 859.88 & 707.85\\ 597.13 & 588.69 & 707.85 & 704.62 \end{pmatrix} \\ \text{SSB}=\begin{pmatrix} 105.27 & 164.01 & 66.91 & 157.12\\ 164.01 & 261.15 & 82.68 & 218.02\\ 66.91 & 82.68 & 124.81 & 202.01\\ 157.12 & 218.02 & 202.01 & 361.31 \end{pmatrix}$$

因此可以计算出Wilks检验统计量:

$$\Lambda=\frac{\vert\text{SSW}\vert}{\vert\text{SSW}+\text{SSB}\vert}=0.1068$$

记

$$F=\frac{n - 2 - p}{p}\cdot\frac{1-\sqrt{\Lambda}}{\sqrt{\Lambda}}=12.3597$$

由于总体个数，有.

因此检验的值为

结论：因为 p 值比 0.05 小得多，所以结论是有显著差异。如选用标准显著性水平 ，显然 p 值小于 0.05；如选用 或更严格标准，p 值依然小于这些标准。显然，我们有非常强的统计证据拒绝原假设，认为 3 种生产方法对完成生产任务有显著差异。

3.3.5 多元均值和方差的同时检验

设有个相互独立的总体，，。

是来自总体的样本，。记，。

考虑检验问题：

$$\begin{cases} H_0:\mu_1=\cdots=\mu_k,\quad\Sigma_1=\cdots=\Sigma_k\\ H_1:\mu_1,\cdots,\mu_k不全相等，或\Sigma_1,\cdots,\Sigma_k不全相等 \end{cases}$$

似然函数为 ：

$$L(\mu_1,\cdots,\mu_k,\Sigma_1,\cdots,\Sigma_k)=\prod_{i = 1}^{k}|\Sigma_i|^{-n_i/2}\exp\left\{-\frac{1}{2}\text{tr}\left(\sum_{i = 1}^{k}\Sigma_i^{-1}[V_i + n_i(\bar{x}_i - \mu_i)(\bar{x}_i - \mu_i)']\right)\right\}$$

先考虑两个似然比 :

$$\begin{align} \lambda_1&=\frac{\sup_{\{\mu_1,\cdots,\mu_k,\Sigma\}}L(\mu_1,\cdots,\mu_k,\Sigma,\cdots,\Sigma)}{\sup_{\{\mu_1,\cdots,\mu_k,\Sigma_1,\cdots,\Sigma_k\}}L(\mu_1,\cdots,\mu_k,\Sigma_1,\cdots,\Sigma_k)} \\ &=\frac{n^{pn/2}\prod_{i = 1}^{k}|V_i|^{n_i/2}}{\prod_{i = 1}^{k}n_i^{pn_i/2}\cdot|\sum_{i = 1}^{k}V_i|^{n/2}}\\\\ \lambda_2&=\frac{\sup_{(\mu,\Sigma)}L(\mu,\cdots,\mu,\Sigma,\cdots,\Sigma)}{\sup_{(\mu_1,\cdots,\mu_k,\Sigma)}L(\mu_1,\cdots,\mu_k,\Sigma,\cdots,\Sigma)} \\ &=\left(\frac{|SSW|}{|SSW + SSB|}\right)^{n/2}\\ &=\left(\frac{|\sum_{i = 1}^{k}V_i|}{|\sum_{i = 1}^{k}\sum_{j = 1}^{n_i}(x_{ij}-\bar{x})(x_{ij}-\bar{x})'|}\right)^{n/2} \end{align}$$

则总似然比为：

$$\begin{align} \lambda&=\frac{\sup_{(\mu,\Sigma)}L(\mu,\cdots,\mu,\Sigma,\cdots,\Sigma)}{\sup_{(\mu_1,\cdots,\mu_k,\Sigma_1,\cdots,\Sigma_k)}L(\mu_1,\cdots,\mu_k,\Sigma_1,\cdots,\Sigma_k)}\\ & =\lambda_1\lambda_2 \\ & =\frac{n^{pn/2}}{\prod_{i = 1}^{k}n_i^{pn_i/2}}\cdot\frac{\prod_{i = 1}^{k}|V_i|^{n_i/2}}{\left|\sum_{i = 1}^{k}\sum_{j = 1}^{n_i}(x_{ij}-\bar{x})(x_{ij}-\bar{x})'\right|^{n/2}} \end{align}$$

很难推导似然比的精确分布，故用其渐近分布，也就是利用Wilks定理。

$$\dim(\Theta)=k(p + p(p + 1)/2)=kp(p + 3)/2 \\ \dim(\Theta_0)=p + p(p + 1)/2\\ \dim(\Theta)-\dim(\Theta_0)=(k - 1)p(p + 3)/2$$

由Wilks定理知 :

$$- 2\log(\lambda)\stackrel{d}{\to}\chi^2((k - 1)p(p + 3)/2) \\ p = \Pr\{\chi^2((k - 1)p(p + 3)/2)\geq - 2\log(\lambda)\}$$

若，则拒绝零假设。

思考下列检验问题：

检验问题	原假设	备择假设
单样本协方差阵检验
单样本均值和协方差阵的联合检验
多总体协方差阵比较问题

参考思路：

1. 计算似然比检验统计量。
2. 再由Wilks定理导出检验统计量的渐近分布。
3. 构造检验方案。

例：检验多总体协方差阵是否相等

问题：3种生成方法的协方差阵是否相等？

即3总体的协方差的比较问题：

$$H_0:\Sigma_1=\Sigma_2=\Sigma_3,\quad v.s.\quad H_1:\Sigma_1,\Sigma_2,\Sigma_3不全相等$$

检验的似然比为：

$$\begin{align} \lambda&=\frac{\sup_{(\mu_1,\mu_2,\mu_3,\Sigma)}L(\mu_1,\mu_2,\mu_3,\Sigma,\Sigma,\Sigma)}{\sup_{(\mu_1,\mu_2,\mu_3,\Sigma_1,\Sigma_2,\Sigma_3)}L(\mu_1,\mu_2,\mu_3,\Sigma_1,\Sigma_2,\Sigma_3)}\\ &=\frac{n^{pn/2}\prod_{i = 1}^{3}|V_i|^{n_i/2}}{\prod_{i = 1}^{3}n_i^{pn_i/2}\cdot|\sum_{i = 1}^{3}V_i|^{n/2}} \end{align}$$

由Wilks定理知 （p=4, k=3, ）:

$$- 2\log(\lambda)\stackrel{d}{\to}\chi^2((k - 1)p(p + 1)/2) \\\\ \begin{align} p &= \Pr\{\chi^2((k - 1)p(p + 1)/2)\geq - 2\log(\lambda)\}\\ &=Pr\{\chi^2(20)\ge-2\log(\lambda)\} \end{align}$$

经计算，有 :

$$|V_1| = 5.0698\times 10^{6}, |V_2| = 4.2057\times 10^{6}, |V_3| = 7.2397\times 10^{5}, \\ |V| = |V_1 + V_2 + V_3| = 5.0218\times 10^{8},\\ - 2\log(\lambda)=24.631\\ p = Pr\{\chi^2(20)\geq - 2\log(\lambda)\}=Pr\{\chi^2(20)\geq 24.631\}=0.2159\gt0.05$$

结论：没有足够证据拒绝零假设，即认为3个总体的协方差阵相等.

3.3.6 独立性检验

设是来自总体的独立样本， 其中。 将和分别剖分为

$$X = \left( \begin{array}{c} X_1\\ \vdots\\ X_m \end{array} \right), \Sigma = \left( \begin{array}{ccc} \Sigma_{11}&\cdots&\Sigma_{1m}\\ \vdots&\ddots&\vdots\\ \Sigma_{m1}&\cdots&\Sigma_{mm} \end{array} \right)$$

其中，，是的矩阵，，。

我们感兴趣的问题是： 是否相互独立？

对应的检验问题为：

$$H_0:\Sigma_{ij} = 0, 1\leq i,\quad v.s.\quad H_1:\Sigma_{ij}不全为0, \quad 1\leq i<j\leq m$$

考虑似然比检验。 似然函数为(去掉常数项) :

$$L(\mu,\Sigma)=\vert\Sigma\vert^{-n/2}\exp\left\{-\frac{1}{2}\text{tr}(\Sigma^{-1}(V + n(\bar{x}-\mu)(\bar{x}-\mu)'))\right\}$$

我们将，和作相应剖分 :

$$\mu=\left(\begin{array}{c} \mu_{1} \\ \vdots \\ \mu_{m} \end{array}\right), \bar{x}=\left(\begin{array}{c} \bar{x}_{1} \\ \vdots \\ \bar{x}_{m} \end{array}\right), V=\left(\begin{array}{ccc} V_{11} & \cdots & V_{1m} \\ \vdots & & \vdots \\ V_{m1} & \cdots & V_{mm} \end{array}\right)$$

在零假设下，似然函数为：

$$L_{0}(\mu_{1},\cdots,\mu_{m},\Sigma_{11},\cdots,\Sigma_{mm})\\ =\prod_{i = 1}^{m}|\Sigma_{ii}|^{-n/2}\exp\left\{-\frac{1}{2}\sum_{i = 1}^{m}\text{tr}(\Sigma_{ii}^{-1}[V_{ii}+n(\bar{x}_{i}-\mu_{i})(\bar{x}_{i}-\mu_{i})'])\right\}$$

则似然比统计量为：

$$\begin{align} \lambda &= \frac{\sup_{(\mu_1,\cdots,\mu_m,\Sigma_{11},\cdots,\Sigma_{mm})} L_0(\mu_1,\cdots,\mu_m,\Sigma_{11},\cdots,\Sigma_{mm})}{\sup_{(\mu,\Sigma)} L(\mu,\Sigma)} \\&= \left( \frac{\left| V \right|}{\prod_{i = 1}^{m}\left| V_{ii} \right|}\right)^{n/2} \end{align}$$

由Wilks定理知

$$- 2 \log(\lambda) \stackrel{d}{\rightarrow} \chi^2\left(\frac{p^2 - \sum_{i = 1}^{m} p_i^2}2\right)$$

其中自由度的计算如下：

$$\dim(\Theta) = p + p(p + 1)/2\\ \dim(\Theta_0) = p + \sum_{i = 1}^{m} p_i(p_i + 1)/2 \\ \dim(\Theta) - \dim(\Theta_0) = \left(p^2 - \sum_{i = 1}^{m} p_i^2\right)/2$$

精确分布

考虑的情形. 此时剖分为维和维两部分，.

相应的似然比为.

又由矩阵的分块运算知

因此

$$\begin{align} \lambda&=\left(\frac{\left|V_{22}-V_{21}V_{11}^{-1}V_{12}\right|}{\left|V_{22}\right|}\right)^{\frac n 2} \\&=\left(\frac{\left|V_{22}-V_{21}V_{11}^{-1}V_{12}\right|}{\left|\left(V_{22}-V_{21}V_{11}^{-1}V_{12}\right)+V_{21}V_{11}^{-1}V_{12}\right|}\right)^{\frac n 2} \end{align}$$

由于，且在零假设下有 ， 由Wishart分布的独立分解性质知: 令，有。

$$\begin{align} \Lambda &= \frac{\vert V_{22}-V_{21}V_{11}^{-1}V_{12}\vert}{\vert(V_{22}-V_{21}V_{11}^{-1}V_{12})+V_{21}V_{11}^{-1}V_{12}\vert}\\ &\stackrel{d}{=} \frac{\vert W_{p_2}(n - 1 - p_1,\Sigma_{22})\vert}{\vert W_{p_2}(n - 1 - p_1,\Sigma_{22})+W_{p_2}(p_1,\Sigma_{22})\vert}\\ &\stackrel{d}{\approx} \Lambda_{p_2,n - 1 - p_1,p_1} \end{align}$$

	服从分布

特别地，当时，似然比和检验统计量分别为 :

$$\begin{align} \lambda&=\left(\frac{|V|}{|V_{11}| \cdot |V_{22}|}\right)^{n / 2}=\left(\frac{v_{11} v_{22}-v_{12}^{2}}{v_{11} v_{22}}\right)^{n / 2} \\ &=\left(1 - \frac{v_{12}^{2}}{v_{11} v_{22}}\right)^{n / 2}=\left(1 - r^{2}\right)^{n / 2}\\ \\ &\frac{n - 1 - p_1}{p_1} \cdot \frac{1 - \lambda^{2 / n}}{\lambda^{2 / n}}=(n - 2) \frac{r^{2}}{1 - r^{2}} \\ &\stackrel{d}{\sim} F(1, n - 2)\\ & \stackrel{d}{=} t^{2}(n - 2) \end{align}$$

例: 独立性检验

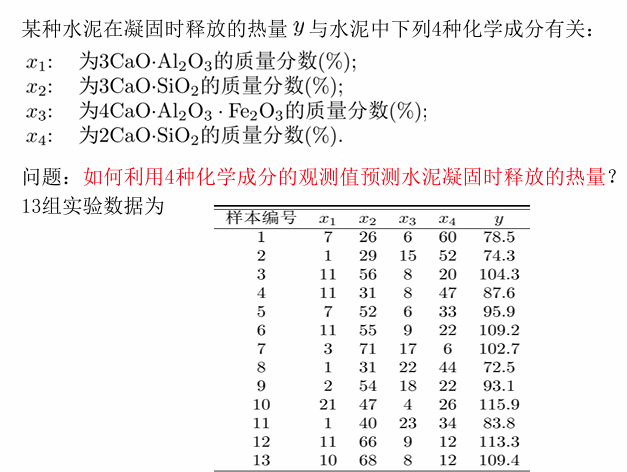
检验问题：是否与相互独立？

的样本离差阵V为：

$$V=\left(\begin{array}{cccc} 415.2&251.1& - 372.6& - 290.0\\ 251.1&2905.7& - 166.5& - 3041.0\\ - 372.6& - 166.5&492.3&38.0\\ - 290.0& - 3041.0&38.0&3362.0 \end{array}\right)\\ V_{11}=\left(\begin{array}{cc} 415.2& - 372.6\\ - 372.6&492.3 \end{array}\right), V_{22}=\left(\begin{array}{cc} 2905.7& - 3041.0\\ - 3041.0&3362.0 \end{array}\right)$$

和的样本离差阵分别为 , 样本量。

计算离差阵的行列式有：, 似然比统计量的值为：

$$\Lambda=\lambda^{\frac 2 n}=\lambda^{\frac 2 13}=\frac{\vert V\vert}{\vert V_{11}\vert · \vert V_{22}\vert}=0.0624$$

由于, 检验统计量、p值为:

$$\frac{n-2-p_1}{p_1}·\frac{1-\sqrt \Lambda}{\sqrt \Lambda}=\frac 9 2·\frac{1- \lambda^{\frac 1 {13}}}{\lambda^{\frac 1 {13}}}=13.514\\\\ \begin{align} p&=Pr\{F(2p_1,2(n-2-p_1))\ge13.514\}\\ &=Pr\{F(4,18)\ge 13.514\}\\ &=2.94\times 10^{-5}<0.05 \end{align}$$

结论：拒绝原假设，认为不与相互独立。

当时，似然比为:

$$\lambda = \left( \frac{\vert V \vert}{\prod_{i = 1}^{p} v_{ii}} \right)^{n/2} = \vert R \vert^{n/2}$$

可由样本相关系数矩阵的分布给出检验方案。

3.3.7 条件独立性检验

将剖分为维和维两部分，，并对作相应剖分，有:

$$X=\begin{pmatrix}X_1\\X_2\end{pmatrix},\quad \Sigma=\begin{pmatrix}\Sigma_{11}&\Sigma_{12}\\\Sigma_{21}&\Sigma_{22}\end{pmatrix}$$

因此，在给定下的条件协方差阵为:

$$T = Cov(X_1|X_2)=\Sigma_{1|2}=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}$$

再将和条件协方差阵作剖分 :

$$X_1=\begin{pmatrix}X_{11}\\\vdots\\X_{1m}\end{pmatrix},\quad T=\begin{pmatrix}T_{11}&\cdots&T_{1m}\\\vdots&\ddots&\vdots\\T_{m1}&\cdots&T_{mm}\end{pmatrix}$$

其中为维向量，, 是的矩阵，。

理解每个为维：

假设我们在研究某种疾病的患者数据，收集了以下几类信息：

:健康指标

: 血压	:血糖水平	: 胆固醇水平
收缩压（Systolic Blood Pressure, SBP）	空腹血糖（Fasting Blood Glucose, FBG）	总胆固醇（Total Cholesterol, TC）
舒张压（Diastolic Blood Pressure, DBP）		高密度脂蛋白胆固醇（High-Density Lipoprotein, HDL）
		低密度脂蛋白胆固醇（Low-Density Lipoprotein, LDL）

X₂人口统计信息: 年龄（Age）、性别（Gender）

变量划分：

总体变量： p=8

• （血压2维，血糖1维，胆固醇3维）。

• （年龄1维，性别1维）。

对有：

$$X_1= \begin{pmatrix} X_{11} \\ X_{12} \\ X_{13} \end{pmatrix},X_{11} = \begin{pmatrix} \text{SBP} \\ \text{DBP} \end{pmatrix},X_{12} = \begin{pmatrix} \text{FBG} \end{pmatrix},X_{13} = \begin{pmatrix} \text{TC} \\ \text{HDL} \\ \text{LDL} \end{pmatrix}$$

所以，有.总的来说，是对一个的多元正态总体的n在不断的划分。

感兴趣的问题是：在给定的条件下，的分量是否相互独立？

对应的检验问题为:

$$H_0:T_{ij} = 0,1\leq i<j\leq m,\quad v.s.\quad H_1:T_{ij}不全为0,\quad1\leq i<j\leq m$$

A. 检验统计量的构造

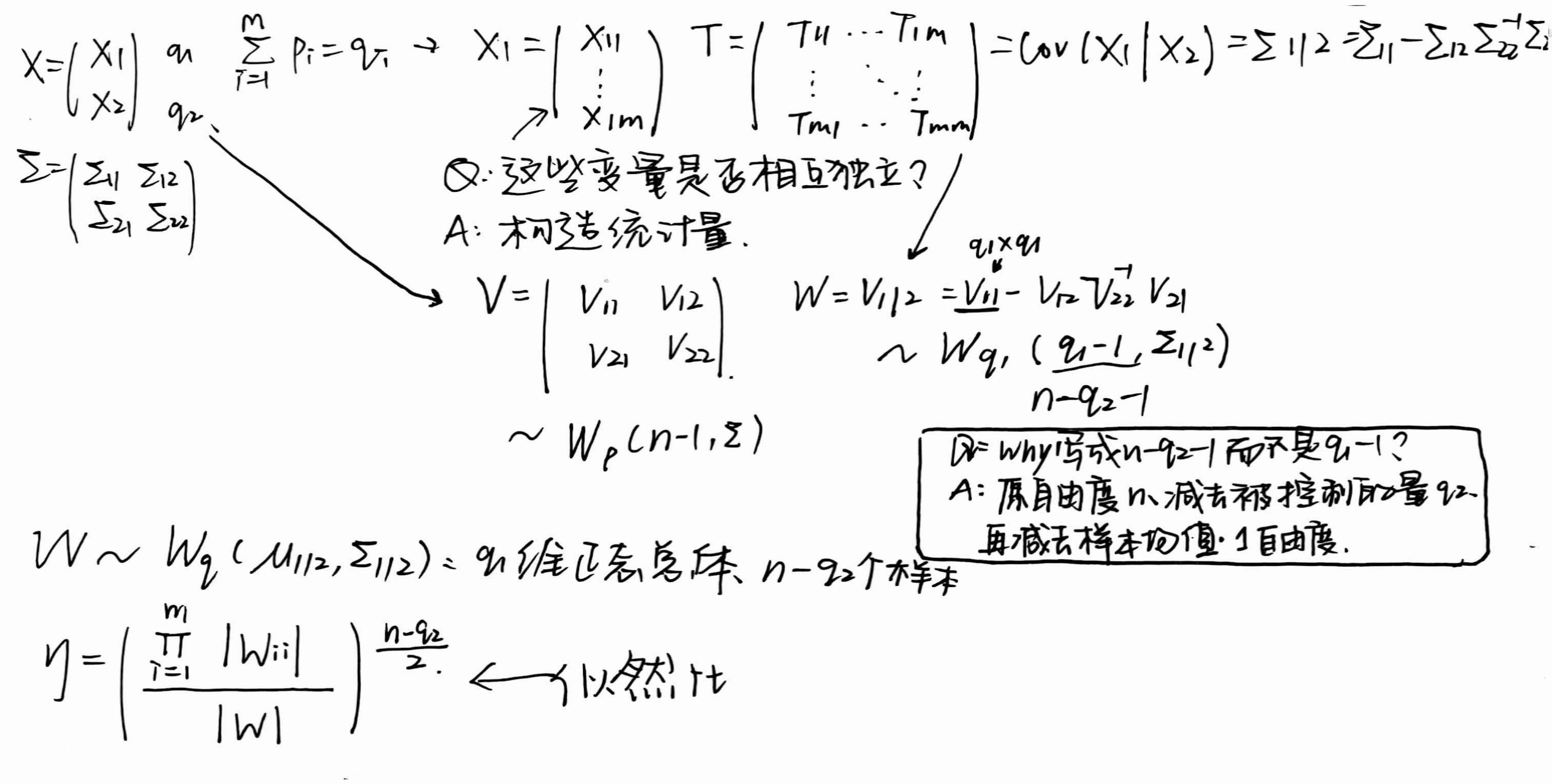
将样本离差阵$V$作相应剖分 $V=\begin{pmatrix}V_{11}&V_{12}\\V_{21}&V_{22}\end{pmatrix}$， 计算在$X_2$给定后$X_1$的样本条件离差阵 $W = V_{1|2}=V_{11}-V_{12}V_{22}^{-1}V_{21}$。

由于$V\stackrel{d}{\sim}W_p(n - 1,\Sigma)$，有 $W\stackrel{d}{\sim}W_{q_1}(n - q_2 - 1,\Sigma_{1|2})$。

注意：此时，$W$可以看成是:

• 均值为 $\mu_{1|2}=E(X_1|X_2=x_2)=\mu_1+\Sigma_{12}\Sigma_{22}^{-1}(x_2-\mu_2)$
• 协方差阵为 $\Sigma_{1|2}=Cov(X_1|X_2=x_2)=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}$

的$q_1$维正态总体的$n - q_2$个(虚拟)独立样本的样本离差阵。

再将样本条件离差阵$W$作相应剖分:

$$W=\begin{pmatrix}W_{11}&\cdots&W_{1m}\\\vdots&\ddots&\vdots\\W_{m1}&\cdots&W_{mm}\end{pmatrix}$$

其中，是的矩阵，。

相似地，基于这组虚拟样本，可得检验的似然比为 :

$$\eta=\left(\frac{\prod_{i = 1}^{m}|W_{ii}|}{|W|}\right)^{-(n - q_2)/2}$$

再利用3.3.6中的独立性检验结果导出检验统计量的精确分布或渐近分布。

例：条件独立性检验

检验问题：给定的条件下，与是否相互独立？

的样本离差阵为 :

$$V=\begin{pmatrix}415.2&251.1&- 372.6&- 290.0&776.0\\251.1&2900.5&- 166.5&- 3041.0&2293.0\\- 372.6&- 166.5&492.3&38.0&- 618.2\\- 290.0&- 3041.0&38.0&3362.0&- 2481.7\\776.0&2293.0&- 618.2&- 2481.7&2715.8\end{pmatrix}$$

经计算，可得给定的条件下，的样本条件离差阵为 :

$$W=\begin{pmatrix}156.68&- 161.08&39.17\\- 161.08&177.51&- 41.99\\39.17&- 41.99&57.91\end{pmatrix}$$

本例中，，，，因此样本量变为虚拟样本量:

$$m=n - q_2=13 - 2 = 11\\ W_{11}=\begin{pmatrix}156.68&- 161.08\\- 161.08&177.51\end{pmatrix},w_{22}=57.91$$

因此，条件独立性检验的似然比的值为 :

$$\begin{align} \lambda&=\left(\frac{\vert W\vert}{\vert W_{11}\vert\cdot\vert w_{22}\vert}\right)^{m/2}=\left(\frac{\vert W\vert}{\vert W_{11}\vert\cdot\vert w_{22}\vert}\right)^{11/2}=0.8256^{11/2}\\\\ \Lambda&=\lambda^{2/m}=0.8256 \end{align}$$

本例中，，，虚拟样本量 检验统计量的值为 :

$$F=\frac{m - 1 - p_1}{p_1}\cdot\frac{1-\Lambda}{\Lambda}=\frac{11 - 1 - 2}{2}\cdot\frac{1 - 0.8256}{0.8256}=0.8397$$

检验的值为 结论：不能拒绝给定的条件下，与相互独立的假设。

作业：两总体均值检验

设 和 是两个相互独立的 维正态总体，其中 未知。设 是来自总体 的 个独立样本， 是来自总体 的 个独立样本，其中 。 请给出如下检验问题的检验方案 :

$$H_0:\mu_1 = -\mu_2,\quad v.s.\quad H_1:\mu_1\neq-\mu_2$$

相等，所以和Berman-Fisher检验问题无关。就是单纯的两总体的均值比较问题，但是注意假设中有负号。

①线性变换：令后续就按最普通的进行计算即可。

②根据似然比做：直接比较在原假设和备择假设下的最大似然值，判断是否拒绝原假设。

在下:

$$\hat\mu_1=\frac{m\bar x-n\bar y}{m+n},\hat\mu_2=\frac{n\bar y-m\bar x}{m+n}\\\\ \hat \Sigma=\frac{1}{m+n}[V+\frac{mn}{m+n}(\bar x+\bar y)(\bar x+\bar y)']$$

题目给出未知，此时样本离差阵. 的似然函数为：

$$L(\mu_1,\mu_2,\Sigma)=\vert\Sigma\vert^{-(m + n)/2}\times\\ \exp\left\{-\frac{1}{2}\text{tr}[\Sigma^{-1}(V + m(\bar{x}-\mu_1)(\bar{x}-\mu_1)' + n(\bar{y}-\mu_2)(\bar{y}-\mu_2)')]\right\}$$

检验问题的似然比为:

$$\begin{align} \lambda&=\frac{\sup_{\{\mu,\Sigma\}}L(\mu,\mu,\Sigma)}{\sup_{\{\mu_1,\mu_2,\Sigma\}}L(\mu_1,\mu_2,\Sigma)}\\ &=\left(\frac{\vert V_1+V_2 + \frac{mn}{m+n}(\bar{x}+\bar{y})(\bar{x}+\bar{y})'\vert}{\vert V_1+V_2\vert}\right)^{-(m + n)/2}\\ &=\left(1+\frac{mn}{m + n}(\bar{x}+\bar{y})'(V_1+V_2)^{-1}(\bar{x}+\bar{y})\right)^{-(m + n)/2} \end{align}$$

令 :

$$T^2=\frac{mn(m + n - 2)}{m + n}(\bar{x}+\bar{y})'V^{-1}(\bar{x}+\bar{y})\\\\ T^2\vert_{H_0}\stackrel{d}{\sim}T^2_p(m + n - 2)$$

因此，当 时拒绝零假设， 其犯第一类错误的概率为 。

Q: 是怎么得到？

A: 通过极大似然估计得到，下面是具体过程。

我们有两个独立的 维正态总体：

其中，协方差矩阵 是相同的且未知的。我们从每个总体中分别抽取了独立的样本：

• 总体 ：样本
• 总体 ：样本

样本量满足 ，以确保检验的有效性。我们要检验的假设为：

$$H_0: \mu_1 = -\mu_2 \quad \text{vs.} \quad H_1: \mu_1 \neq -\mu_2$$

步骤1：构造似然函数: 对于两个总体 和 ，其联合似然函数为两个独立正态分布的乘积：

$$L(\mu_1, \mu_2, \Sigma) = L_X(\mu_1, \Sigma) \times L_Y(\mu_2, \Sigma)\\ L_X(\mu_1, \Sigma) = \prod_{i=1}^m \frac{1}{(2\pi)^{p/2} |\Sigma|^{1/2}} \exp\left( -\frac{1}{2} (x_i - \mu_1)^\top \Sigma^{-1} (x_i - \mu_1) \right)\\ L_Y(\mu_2, \Sigma) = \prod_{j=1}^n \frac{1}{(2\pi)^{p/2} |\Sigma|^{1/2}} \exp\left( -\frac{1}{2} (y_j - \mu_2)^\top \Sigma^{-1} (y_j - \mu_2) \right)\\ L(\mu_1, \mu_2, \Sigma) = \frac{1}{(2\pi)^{(m+n)p/2} |\Sigma|^{(m+n)/2}} \exp\left( -\frac{1}{2} \left[ \sum_{i=1}^m (x_i - \mu_1)^\top \Sigma^{-1} (x_i - \mu_1) + \sum_{j=1}^n (y_j - \mu_2)^\top \Sigma^{-1} (y_j - \mu_2) \right] \right)\\$$

步骤2：对数似然函数为了简化计算，我们取对数似然函数：

$$\begin{align} &\ell(\mu_1, \mu_2, \Sigma)= \log L(\mu_1, \mu_2, \Sigma) \\ &=-\frac{(m+n)p}{2} \log(2\pi) - \frac{(m+n)}{2} \log |\Sigma| - \frac{1}{2} \left[ \sum_{i=1}^m (x_i - \mu_1)^\top \Sigma^{-1} (x_i - \mu_1) + \sum_{j=1}^n (y_j - \mu_2)^\top \Sigma^{-1} (y_j - \mu_2) \right] \end{align}$$

步骤3：在原假设 下最大化似然函数: 在原假设 下，我们有 。因此，对数似然函数变为：

$$\ell(\mu_1, \Sigma) = -\frac{(m+n)p}{2} \log(2\pi) - \frac{(m+n)}{2} \log |\Sigma| - \frac{1}{2} \left[ \sum_{i=1}^m (x_i - \mu_1)^\top \Sigma^{-1} (x_i - \mu_1) + \sum_{j=1}^n (y_j + \mu_1)^\top \Sigma^{-1} (y_j + \mu_1) \right]\\\\$$

求导：

$$\begin{align} \frac{\partial \ell}{\partial \mu_1} = \sum_{i=1}^m \Sigma^{-1} (x_i - \mu_1) - \sum_{j=1}^n \Sigma^{-1} (y_j + \mu_1) &= 0\\ \sum_{i=1}^m (x_i - \mu_1) &= \sum_{j=1}^n (y_j + \mu_1)\\ \sum_{i=1}^m x_i - m\mu_1 &= \sum_{j=1}^n y_j + n\mu_1\\ \sum_{i=1}^m x_i - \sum_{j=1}^n y_j &= (m + n)\mu_1\\ \mu_1 = \frac{\sum_{i=1}^m x_i - \sum_{j=1}^n y_j}{m + n} &= \frac{m\bar{x} - n\bar{y}}{m + n} \end{align}$$

由于 ，则

对 的求偏导数同理。

1. 对数似然函数中涉及 的部分：

$$-\frac{(m+n)}{2} \log |\Sigma| - \frac{1}{2} \text{tr}\left[ \Sigma^{-1} \left( \sum_{i=1}^m (x_i - \mu_1)(x_i - \mu_1)^\top + \sum_{j=1}^n (y_j + \mu_1)(y_j + \mu_1)^\top \right) \right]$$

1. 对 的偏导数为零：

$$-\frac{(m+n)}{2} \Sigma^{-1} + \frac{1}{2} \Sigma^{-1} \left( \sum_{i=1}^m (x_i - \mu_1)(x_i - \mu_1)^\top + \sum_{j=1}^n (y_j + \mu_1)(y_j + \mu_1)^\top \right) \Sigma^{-1} = 0$$

1. 解得：

$$\begin{align} \Sigma &= \frac{1}{m + n} \left( \sum_{i=1}^m (x_i - \mu_1)(x_i - \mu_1)^\top + \sum_{j=1}^n (y_j + \mu_1)(y_j + \mu_1)^\top \right)\\ \hat{\Sigma} &= \frac{1}{m + n} \left[ V_X + V_Y + \frac{mn}{m + n} (\bar{x} + \bar{y})(\bar{x} + \bar{y})^\top \right]\\ V_X &= \sum_{i=1}^m (x_i - \bar{x})(x_i - \bar{x})^\top, \quad V_Y = \sum_{j=1}^n (y_j - \bar{y})(y_j - \bar{y})^\top \end{align}$$