多元统计分析-Ch3 多元正态分布的估计与检验

【挑战20天学完多元统计分析，让我们说：DDL是最佳生产力！】

急，只剩下10天了。。。

Ch3 多元正态分布的估计与检验

[TOC]

3.1 多元正态分布样本统计量

设为来自多元正态总体的独立样本，其中，，。记:

metric	公式	说明
样本均值		无偏估计，即。
样本离差阵		衡量了样本点相对于样本均值的离散程度。
样本协方差阵		对离差阵进行归一化

事实：是的完全充分统计量, 这意味着和包含了样本中关于总体参数和的所有信息。

3.1.1 (, ) 的分布性质

1. ；
2. ；
3. 与 相互独立。

证明：

（1）记 ，则有 ，。

令 为 阶正交矩阵，其中:

$$U_1 = \left( \frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}, \cdots, \frac{1}{\sqrt{n}} \right)' = \frac{1}{\sqrt{n}} \mathbf{1}_n\\ 1_n'U_j=\sqrt{n}(\frac 1 {\sqrt{n}}1_n)'U_j=\sqrt{n}U_iU_j=0$$

的第一列 被特别选择为与样本均值方向相关的向量。令 记为 ，则代表了样本均值方向上的信息, 则代表了与样本均值正交的剩余信息。

$$E(Y) = E(X)U = \mu \mathbf{1}_n'U = \mu \mathbf{1}_n'\left( \frac{1}{\sqrt{n}} \mathbf{1}_n, U_2, \cdots, U_n \right) = (\sqrt{n} \mu, 0, \cdots, 0)\\ \begin{align*} \text{Cov}(\text{vec}(Y))&=\text{Cov}(\text{vec}(I_p XU))\\ &=\text{Cov}((U' \otimes I_p)\text{vec}(X))\\ &=(U' \otimes I_p)\text{Cov}(\text{vec}(X))(U \otimes I_p)\\ &=(U' \otimes I_p)(I_n \otimes \Sigma)(U \otimes I_p)\\ &=I_n \otimes \Sigma \end{align*}$$

从上面的可以得到：相互独立，且， 。 因而有，即(1)成立。

（2）由于，即，因而有

$$\begin{align*} V&=\sum_{i = 1}^{n}X_iX_i'-n\bar{X}\bar{X}'\\ &=\sum_{i = 1}^{n}X_iX_i'-Y_1Y_1'\\ &=\sum_{i = 1}^{n}Y_iY_i'-Y_1Y_1'\\ &=\sum_{i = 2}^{n}Y_iY_i'\sim W_p(n - 1,\Sigma)\end{align*}$$

所以(2)成立。 又由于，，因此与独立，即(3)成立。

3.2 多元正态分布的参数估计

3.2.1 极大似然估计

观测样本的联合密度：

$$f(X)=(2\pi)^{-\frac{n p}{2}}|\Sigma|^{-\frac{n}{2}}\exp\left\{-\frac{1}{2}\text{tr}\Sigma^{-1}(V + n(\bar{X}-\mu)(\bar{X}-\mu)')\right\}$$

首先求的极大似然估计:

$$\begin{align} f(X)&=(2\pi)^{-\frac{n p}{2}}|\Sigma|^{-\frac{n}{2}}\exp\left\{-\frac{1}{2}\text{tr}\Sigma^{-1}(V + n(\bar{X}-\mu)(\bar{X}-\mu)')\right\}\\ &=(2\pi)^{-\frac{n p}{2}}|\Sigma|^{-\frac{n}{2}}\exp\left\{-\frac{1}{2}\text{tr}\Sigma^{-1}V-\frac{n}{2}\text{tr}\Sigma^{-1}(\bar{X}-\mu)(\bar{X}-\mu)'\right\}\\ &=(2\pi)^{-\frac{n p}{2}}|\Sigma|^{-\frac{n}{2}}\exp\left\{-\frac{1}{2}\text{tr}\Sigma^{-1}V-\frac{n}{2}(\bar{X}-\mu)'\Sigma^{-1}(\bar{X}-\mu)\right\} \end{align}$$

易知的极大似然估计为：。 即正态总体均值的极大似然估计是样本均值。

将代入似然函数并去掉与参数无关的项，有：

$$f(X)\propto|\Sigma|^{-n/2}\exp\left\{-\frac{1}{2}\text{tr}(\Sigma^{-1}V)\right\}$$

考虑正交分解，其中是正交矩阵， 。那么有:

$$|\Sigma|^{-1}=|V|^{-1}\prod_{i = 1}^{p}\lambda_i,\\ \text{tr}(\Sigma^{-1}V)=\text{tr}(\Sigma^{-1/2}V\Sigma^{-1/2})=\text{tr}(UAU')=\text{tr}(AU'U)=\text{tr}(\Lambda)=\sum_{i = 1}^{p}\lambda_i.$$

则上面的式子变为：

$$f(X)\propto|\Sigma|^{-n/2}\exp\left\{-\frac{1}{2}\text{tr}(\Sigma^{-1}V)\right\}\\ f(X)\propto|V|^{-n/2}\prod_{i = 1}^{p}\lambda_i^{n/2}\exp\left\{-\frac{\lambda_i}{2}\right\}$$

上式在时取最大值，故的极大似然估计满足：

$$\hat{\Sigma}^{-1/2}V\hat{\Sigma}^{-1/2}=nI_p\Rightarrow\hat{\Sigma}=V/n$$

因此，正态总体参数的极大似然估计为。 记 :

—-	公式	期望
样本协方差阵
样本精度矩阵

因此，是的无偏估计(一致最小)。

3.2.2 样本相关系数

记为正态总体的相关系数矩阵，并记，，则的极大似然估计为:

$$\hat{\rho}_{ij}=r_{ij}=\frac{v_{ij}}{\sqrt{v_{ii}v_{jj}}}=\frac{s_{ij}}{\sqrt{s_{ii}s_{jj}}}, \quad 1\leq i,j\leq p$$

记为样本相关系数矩阵。

A. 样本相关系数的精确分布

考虑二元正态分布的情形: 精确分布假设总体，由性质3.2.7（边际分布：）可知：服从二元正态分布:

$$\ \begin{pmatrix}X_1\\X_2\end{pmatrix}\sim N_2\left(\begin{pmatrix}\mu_1\\\mu_2\end{pmatrix},\begin{pmatrix}\sigma^2_1&\rho\sigma_1\sigma_2\\\rho\sigma_1\sigma_2&\sigma^2_2\end{pmatrix}\right) \\ \rho=\frac{Cov(X_1,X_2)}{\sigma_1\sigma_2},\sigma_1=\sqrt{Var(X_1)},\sigma_2=\sqrt{Var(X_2)}$$

假设下面的样本来自二元分布总体：

$$\begin{pmatrix} x_{11}\\x_{12} \end{pmatrix},\begin{pmatrix} x_{21}\\x_{22} \end{pmatrix},\dots,\begin{pmatrix} x_{n1}\\x_{n2} \end{pmatrix}$$

由这些样本可以定义样本离差阵:

$$V=\begin{pmatrix} v_{11}&v_{12}\\ v_{21}&v_{22} \end{pmatrix}=\begin{pmatrix} \sum^n_{i=1}(x_{i1}-\bar x_1)^2 &\sum^n_{i=1}(x_{i1}-\bar x_1)(x_{i2}-\bar x_2) \\ \sum^n_{i=1}(x_{i1}-\bar x_1)(x_{i2}-\bar x_2) &\sum^n_{i=1}(x_{i2}-\bar x_2)^2 \end{pmatrix}$$

其中样本均值为.

根据相关系数的极大似然估计即为样本相关系数：

$$\hat\rho_{ij}=\frac{\sum^n_{k=1}(x_{ki}-\bar x_i)(x_{kj}-\bar x_j)}{\sqrt{\sum^n_{k=1}(x_{ki}-\bar x_i)^2\sum^n_{k=1}(x_{kj}-\bar x_j)^2}}\equiv r_{ij}\\ r=\frac{\sum^n_{k=1}(x_{k1}-\bar x_1)(x_{k2}-\bar x_2)}{\sqrt{\sum^n_{k=1}(x_{k1}-\bar x_1)^2\sum^n_{k=1}(x_{k2}-\bar x_2)^2}}=\frac{v_{12}}{\sqrt{v_{11}v_{22}}}$$

样本相关系数r与分布的参数无关。令：

$$u_{i1}=\frac{x_{i1}-\mu_1}{\sigma_1},\mu_{i2}=\frac{x_{i2}-\mu_{2}}{\sigma_2},i=1,2,\dots,n$$

则i.i.d.,.

则 :

$$r=\frac{\sum^n_{k=1}(x_{k1}-\bar x_1)(x_{k2}-\bar x_2)}{\sqrt{\sum^n_{k=1}(x_{k1}-\bar x_1)^2\sum^n_{k=1}(x_{k2}-\bar x_2)^2}}=\frac{\sum^n_{k=1}(u_{k1}-\bar u_1)(u_{k2}-\bar u_2)}{\sqrt{\sum^n_{k=1}(u_{k1}-\bar u_1)^2\sum^n_{k=1}(u_{k2}-\bar u_2)^2}}=$$

所以, r 的分布与分布的参数无关，只与有关。

不妨假设，因为样本离差阵，其中 .

$$V=\sum^n_{i=2}Y_iY_i'，Y=[Y_1,Y_2,\dots,Y_n]\\ v_{ij}=\sum^n_{k=2}y_{ki}y_{jk}$$

（是因为n-1,去除一个第一列相关量）

再由Wishart分布的定义知，随机向量的密度函数为:

$$\frac{(v_{xx}v_{yy}-v_{xy}^2)^{(n - 4)/2}}{2^{n - 1}\pi^{1/2}\Gamma\left(\frac{n - 1}{2}\right)\Gamma\left(\frac{n - 2}{2}\right)(1 - \rho^2)^{(n - 1)/2}}\exp\left\{-\frac{v_{xx}+v_{yy}-2\rho v_{xy}}{2(1 - \rho^2)}\right\}$$

其中，，，。

由变换导出的密度函数，再对和积分后，可得的密度函数为:

$$f(r|\rho, n)=\frac{2^{n - 3}(1 - \rho^2)^{(n - 1)/2}(1 - r^2)^{(n - 4)/2}}{\pi(n - 3)!}\sum_{k = 0}^{\infty}\frac{(2\rho r)^k}{k!}\Gamma^2\left(\frac{n + k - 1}{2}\right), \quad |r|<1$$

当时，即与独立，样本相关系数的密度函数为 :

$$f(r|n)=\frac{2^{n - 3}(1 - r^2)^{(n - 4)/2}}{\pi(n - 3)!}\Gamma^2\left(\frac{n - 1}{2}\right), \quad |r| < 1$$

因此，可以用此分布作为, 零假设为与独立时的统计量的零分布, 来检验零假设是否成立。

(书P124-定理5.4.1)：假设是来自p元正态分布的i.i.d.样本，如果，则样本相关系数的密度函数为：

$$f(r|n)=\frac{2^{n - 3}(1 - r^2)^{(n - 4)/2}}{\pi(n - 3)!}\Gamma^2\left(\frac{n - 1}{2}\right), \quad |r| < 1$$

应用：的假设检验

检验问题：(双侧检验：检验变量之间是否存在任何形式的相关性：正相关或负相关) 与独立

等价于：

$$H_0:\rho = 0,\quad v.s.\quad H_1:\rho \neq 0$$

检验方案一： 计算出C，比较r与C的大小。

1. 给定显著性水平 （通常取为0.05）；
2. 计算临界值 ，满足
3. 如果 ，则拒绝零假设，即认为 与 不独立。

检验方案二： 换另外一种方式来确定C：转换为查表计算的t值

通常采用统计量 作为检验与是否独立的统计量。

将相关系数带入得：

$$T = \sqrt{n - 2} \cdot \frac{v_{xy}v_{xx}^{-1/2}}{\sqrt{v_{yy} - v_{xy}^2v_{xx}^{-1}}}$$

由Wishart分布的性质6( 独立分解性质 )知, 当与独立，即时，有 :

• 与相互独立；
• ；
• ；

t分布：为服从自由度为n的t分布。

$$t=\frac{X}{\sqrt{\frac{Y}n}}\sim t(n)$$

在零假设()下：

$$\begin{align} T &= \sqrt{n - 2} \cdot \frac{r}{\sqrt{1 - r^2}} = \frac{v_{xy}v_{xx}^{-1/2}}{\sqrt{\frac{v_{yy}-v_{xy}^2v_{xx}^{-1}}{n - 2}}}\\ &\stackrel{d}{=} \frac{N_1(0,1)}{\sqrt{\frac{\chi^2(n - 2)}{n - 2}}}\\ &\stackrel{d}{\sim}t(n - 2) \end{align}$$

总结检验方案二：

$$H_0: \rho = 0, \quad v.s. \quad H_1: \rho \neq 0,$$

1. 给定显著性水平 ;
2. 如果 ，则拒绝零假设，即认为与不独立， 其中是自由度为的标准分布的分位点。

检验方案三：单侧正/负相关检验：检验变量之间是否存在正/负相关。

独立 vs 正相关的检验问题	独立 vs 负相关的检验问题
计算检验的值:	计算检验的值:
如果值小于显著性水平( )，则拒绝零假设。	如果值小于显著性水平( )，则拒绝零假设。

例子(栗子，吃一口)

在Ch1中的栗子继续拿来讨论：

(1)变量与独立与正相关检验问题

检验统计量为

$$\begin{align} T &= \sqrt{n - 2} \cdot \frac{r}{\sqrt{1 - r^2}} \\ &= \sqrt{13 - 2} \cdot \frac{0.030}{\sqrt{1 - 0.030^2}} \\ &=0.0995 \end{align}$$

因此，变量与独立与正相关检验问题：

$$p = P\{t(11) \geq 0.0995\} = 0.4612 > 0.05,$$

故而不能拒绝与之间的相互独立性。(接受)

(2) 变量与独立与负相关检验问题：

$$p = P\{t(11) \leq - 0.4655\} = 0.3253 > 0.05,$$

则不能拒绝与之间的相互独立性。 (接受)

(3) 变量与独立与负相关检验问题：

$$p = P\{t(11) \leq - 2.1\} = 0.0298 < 0.05,$$

则拒绝与之间的相互独立性，认为它们负相关。(拒绝)

B. 样本相关系数的渐近分布（总体不服从正态分布）

注意到，样本相关系数可以改写成

$\begin{align} v_{xy} &= \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \ &= \frac{1}{n} \sum_{i=1}^{n} x_i y_i - \frac{1}{n} \sum_{i=1}^{n} x_i \bar{y} - \frac{1}{n} \sum_{i=1}^{n} y_i \bar{x} + \frac{1}{n} \sum_{i=1}^{n} \bar{x} \bar{y} \ &= \frac{1}{n} \sum_{i=1}^{n} x_i y_i - \bar{x} \bar{y} - \bar{y} \bar{x} + \bar{x} \bar{y} \ &= \frac{1}{n} \sum_{i=1}^{n} x_i y_i - \bar{x} \bar{y} \ &= t_5 - t_1 t_2 \end{align}$	$\begin{align}v_{xx}&= \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 \&= \frac{1}{n} \sum_{i=1}^{n} (x_i^2 - 2 x_i \bar{x} + \bar{x}^2) \&= \frac{1}{n} \sum_{i=1}^{n} x_i^2 - 2 \bar{x} \cdot \frac{1}{n} \sum_{i=1}^{n} x_i + \frac{1}{n} \sum_{i=1}^{n} \bar{x}^2 \&= \frac{1}{n} \sum_{i=1}^{n} x_i^2 - 2 \bar{x} \cdot \bar{x} + \bar{x}^2 \&= \frac{1}{n} \sum_{i=1}^{n} x_i^2 - \bar{x}^2 \&= t_3 - t_1^2\end{align}$	$\begin{align}v_{yy}&= \frac{1}{n} \sum_{i=1}^{n} (y_i - \bar{y})^2 \&= \frac{1}{n} \sum_{i=1}^{n} (y_i^2 - 2 y_i \bar{y} + \bar{y}^2) \&= \frac{1}{n} \sum_{i=1}^{n} y_i^2 - 2 \bar{y} \cdot \frac{1}{n} \sum_{i=1}^{n} y_i + \frac{1}{n} \sum_{i=1}^{n} \bar{y}^2 \&= \frac{1}{n} \sum_{i=1}^{n} y_i^2 - 2 \bar{y} \cdot \bar{y} + \bar{y}^2 \&= \frac{1}{n} \sum_{i=1}^{n} y_i^2 - \bar{y}^2 \&= t_4 - t_2^2\end{align}$

$$r = \frac{v_{xy}}{\sqrt{v_{xx}v_{yy}}}= \frac{t_5 - t_1 t_2}{\sqrt{t_3 - t_1^2} \cdot \sqrt{t_4 - t_2^2}} = g(t_1, t_2, t_3, t_4, t_5)\\ \begin{cases} t_1 = n^{-1} \sum_{i = 1}^{n} x_i, \\ t_2 = n^{-1} \sum_{i = 1}^{n} y_i,\\ t_3 = n^{-1} \sum_{i = 1}^{n} x_i^2,\\ t_4 = n^{-1} \sum_{i = 1}^{n} y_i^2,\\ t_5 = n^{-1} \sum_{i = 1}^{n} x_iy_i. \end{cases}$$

记随机变量序列，， 并令：

$$\bar{Z} = n^{-1}\sum_{i = 1}^{n}z_i=(t_1,t_2,t_3,t_4,t_5)'.$$

由于 i.i.d.，因此由独立同分布随机变量和的中心极限定理知：

当样本量 增加时，样本均值向量 的分布会趋近于多元正态分布，无论原始随机向量 的分布形态如何，前提是每个 有有限的期望和协方差。

定理（多元中心极限定理）： 设 是一组相互独立且同分布（i.i.d.）的 p维随机向量，具有期望向量和协方差矩阵 。当 n 足够大时，标准化的样本均值向量近似服从多元正态分布 ，即

$$\sqrt{n} (\bar{\mathbf{Z}} - \boldsymbol{\mu}) \xrightarrow{d} N_p(\mathbf{0}, \boldsymbol{\Sigma})$$

其中，是样本均值向量。

引入渐进分布：

令：，是经过标准化的协方差项，是样本协方差，是样本方差。

令，

给出.这个分布的均值为0，协方差为.

$$\Sigma=\begin{pmatrix}2&2\rho^2&2\rho\\2\rho^2&2&2\rho\\2\rho&2\rho&1+\rho^2\end{pmatrix}$$

(书p133 定理5.4.3)令是一列p维的随机向量，b是一个p维固定向量，当,使得, 此处.

假设是一个向量值函数，其中每个分量在处有非零矩阵，定义矩阵，其元素为. 当,使得:

$$\sqrt{n}[f(U(n))-f(b)]\overset{d}{\rightarrow}N_m(0,\Phi_b'\Sigma\Phi_b)$$

上面的的计算有些复杂，换一个来验证一下这个定理：

$$\begin{align} &r=\frac{u_3}{\sqrt{u_1u_2}}\\ &\frac{\partial r}{\partial u_1}|_{u=b}=-\frac 1 2 u_3u_2 (u_1u_2)^{-\frac 3 2}\\ &\frac{\partial r}{\partial u_2}|_{u=b}=-\frac 1 2 u_3u_1 (u_1u_2)^{-\frac 3 2}\\ &\frac{\partial r}{\partial u_3}|_{u=b}=(u_1u_2)^{-\frac 1 2}\\ &f(b)=f(\begin{pmatrix}1\\1\\\rho\end{pmatrix})=\rho代入：\\ &\frac{\partial r}{\partial u_1}|_{u=b}=-\frac 1 2\rho\\ &\frac{\partial r}{\partial u_2}|_{u=b}=-\frac 1 2\rho\\ &\frac{\partial r}{\partial u_3}|_{u=b}=1\\ \end{align}$$

让我们回到：:

$$\sqrt{n}(\bar{Z}-\mu_Z)\stackrel{d}{\rightarrow}N_5(0,\Sigma_Z)\\ \mu_Z = E(z_1)=\begin{pmatrix} 0\\ 0\\ 1\\ 1\\ \rho \end{pmatrix}, \Sigma_Z = \text{Cov}(z_1)=\begin{pmatrix} 1 & \rho & 0 & 0 & 3\rho\\ \rho & 1 & 0 & 0 & 3\rho\\ 0 & 0 & 2\rho^2 & 2\rho^2 & 2\rho\\ 0 & 0 & 2\rho^2 & 2\rho^2 & 2\rho\\ 3\rho & 3\rho & 2\rho & 2\rho & 1+\rho^2 \end{pmatrix}$$

此时有将统计量映射到上的变换g，其中g是在期望处可微。

$$\begin{cases} g(\bar{Z}) = g(t_1, t_2, t_3, t_4, t_5) = r\\ g(\mu_Z) = \rho \end{cases}$$

再由Cramér定理（定理5.4.3），可得样本相关系数的渐近分布：

$$\begin{align} \sqrt{n}(r - \rho) &= \sqrt{n}(g(\bar{Z}) - g(\mu_Z)) \\&\stackrel{d}{\rightarrow} N(0, (g'(\mu_Z))'\Sigma_Z g'(\mu_Z))\\ &\stackrel{d}{\rightarrow} N(0, (1 - \rho^2)^2) \end{align}$$

其中是的一阶偏导。 注意：上面的结论与是否为0无关。

Q: Cramer定理？（Delta方法）

A: 在上面定理5.4.3有提到，总的来说，假设我们有一个大样本的均值向量,且它的分布趋近于正态分布（由中心极限定理可以得到），那么这个均值向量可以应用一个可微函数 ，经过变换后的量也会趋于正态分布。

C. 置信区间(区间估计)

由于样本相关系数的精确分布不是分布自由的，即与未知的总体相关系数有关，因此无法用于置信区间的构造。

因此使用其渐近分布构造总体相关系数的区间估计。但是渐进方差包含未知参数, 因此很难直接利用渐进正态分布来构造的置信区间。为解决这个问题，采用下面两种方法。

(1) plug-in插入方法

既然渐进方差包含未知参数, 可用其极大似然估计进行替换。

当，可以证明, 然后由Slutsky定理有：

$$\frac{\sqrt{n}[r(n)-\rho]}{1-r^2(n)}=\frac{\sqrt{n}[r(n)-\rho]}{1-\rho^2}\frac{1-\rho^2}{1-r^2(n)}\stackrel{d}{\rightarrow} N(0, 1),n\rightarrow \infty$$

因此，总体相关系数的置信水平为的区间估计为 ：

$$\left[r - \frac{(1 - r^2)Z_{1 - \alpha/2}}{\sqrt{n}}, r + \frac{(1 - r^2)Z_{1 - \alpha/2}}{\sqrt{n}}\right]$$

其中是标准正态分布的分位点。

置信区间的统计意义

记： 表示概率。

$$C_L = r - n^{-1/2}(1 - r^2)Z_{1-\alpha/2}\\ C_U = r + n^{-1/2}(1 - r^2)Z_{1-\alpha/2}\\ \begin{align} \Pr\{C_L \leq \rho \leq C_U\} &= \Pr\left\{\left|\frac{\sqrt{n}(r - \rho)}{1 - r^2}\right| \leq Z_{1-\alpha/2}\right\}\\ &\approx \Pr\{|N(0, 1)| \leq Z_{1-\alpha/2}\}\\ &= 1 - \alpha \end{align}$$

是栗子，我们有救了

(1) 变量与的相关系数的置信区间:

$$\begin{align} C_L &= r - n^{-1/2}(1 - r^2)Z_{1 - \alpha/2} \\ & = 0.030 - 13^{-1/2}(1 - 0.030^2) \times 1.96 \\ &= -0.513\\ C_U& = r + n^{-1/2}(1 - r^2)Z_{1 - \alpha/2} \\ &= 0.030 + 13^{-1/2}(1 - 0.030^2) \times 1.96\\ &= 0.573 \end{align}$$

变量	置信区间	相互独立性
变量与的相关系数		0在此区间里，故不能拒绝与之间的相互独立性。
变量与的相关系数		0在此区间里，故也不能拒绝与之间的相互独立性。
变量与的相关系数		0不在此区间里，故不能认为与之间是相互独立的。

(2) 方差齐性变换(Fisher Z变换)

求函数, 使得的渐进方差为1，即：

$$\sqrt{n}[f(r(n))-f(\rho)]\overset{d}{\rightarrow}N(0,1)\\ \sqrt{n}[f(r(n))-f(\rho)]\overset{d}{\rightarrow}N(0,(f'(\rho))^2(1-\rho^2)^2)\\$$

所以：，通过这个计算出函数式子为：,代入上式：

$$\sqrt{n} \left( \frac{1}{2} \ln \frac{1 + r}{1 - r} - \frac{1}{2} \ln \frac{1 + \rho}{1 - \rho} \right) \stackrel{d}{\rightarrow} N(0, 1)$$

由上式可以构造置信水平为的置信区间为：

$$\left[\frac12\ln\frac{1+r(n)}{1-r(n)}]-\frac{1}{\sqrt{n}}z_{1-\alpha/2},\frac12\ln\frac{1+r(n)}{1-r(n)}]+\frac{1}{\sqrt{n}}z_{1-\alpha/2}\right]$$

为构造的置信区间，对上面的置信区间进行变换，可得到的置信水平为的置信区间为

$$\left[ \frac{\frac{1 + r}{1 - r}e^{-a}-1}{\frac{1 + r}{1 - r}e^{-a}+1}, \frac{\frac{1 + r}{1 - r}e^{a}-1}{\frac{1 + r}{1 - r}e^{a}+1} \right] ,a = \frac{2}{\sqrt{n}}Z_{1 - \alpha/2}$$

称为Fisher的变换。通常使用Fisher Z变换方法构造的置信区间。

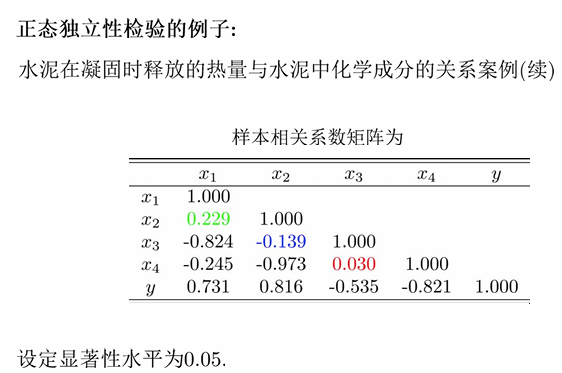
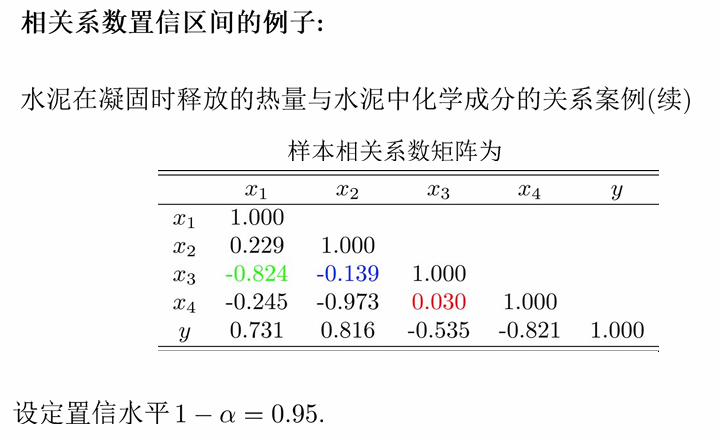
栗子

水泥在凝固时释放的热量与水泥中化学成分的关系案例(续) 设定置信水平。

变量与的相关系数的置信区间的计算：

$$\left[ \frac{\frac{1 + 0.030}{1 - 0.030}e^{-a}-1}{\frac{1 + 0.030}{1 - 0.030}e^{-a}+1}, \frac{\frac{1 + 0.030}{1 - 0.030}e^{a}-1}{\frac{1 + 0.030}{1 - 0.030}e^{a}+1} \right] = [-0.237, 0.293]$$

其中。

变量	置信区间
变量与的相关系数
变量与的相关系数
变量与的相关系数

注意：置信区间变窄。

3.2.3 正态总体均值的置信域估计

A.单总体

设是来自p元正态总体的随机样本，其中. 上面给出了总体均值向量和总体协方差矩阵的无偏估计分别是样本均值向量和样本协方差矩阵. 下面讨论的置信域估计问题，分别在总体协方差阵已知和未知的两种情况下讨论。

已知

如果总体协方差矩阵 已知，样本均值向量 的分布可以通过标准化后的形式来推导出：

$$n(\bar{\mathbf{X}} - \boldsymbol{\mu})'\boldsymbol{\Sigma}^{-1}(\bar{\mathbf{X}} - \boldsymbol{\mu}) \stackrel{d}{\rightarrow} \chi^2(p)$$

则的水平为的置信域估计为：

$$D = \left\{\boldsymbol{\mu} \in \mathbb{R}^p : n(\bar{\mathbf{X}} - \boldsymbol{\mu})'\boldsymbol{\Sigma}^{-1}(\bar{\mathbf{X}} - \boldsymbol{\mu}) \leq \chi^2_{1 - \alpha}(p)\right\}$$

即有 . 意味着在大量的重复实验中，置信域 将包含真实总体均值 的概率为 。

Q: 分布与置信域的联系？

A: 具体来说，样本均值 和总体均值 之间的偏差经过标准化后（即通过协方差矩阵的逆来标准化）符合 分布。这意味着，我们可以通过卡方分布的分位点来构建置信区间。

置信域 D中是卡方分布自由度为 时，置信度为 的分位点。这表示总体均值 在给定的样本数据下落入该置信域的概率为 。

未知

因为我们无从得知，所以使用的无偏估计来代替。令 ：

$$\begin{align} T^2 &= n(\bar{X} - \mu)'S^{-1}(\bar{X} - \mu)\\ &=n(n - 1)(\bar{X} - \mu)'V^{-1}(\bar{X} - \mu)\\ &\sim T^2_p(n-1) \end{align}$$

由正态样本统计量的性质知 ：, , 且与独立.

Hotelling 分布性质如下：

性质	说明
1.	,其中分子分母相互独立；
2.

因此有：

$$T^2 = (n - 1)(\sqrt{n}(\bar{X} - \mu))'V^{-1}(\sqrt{n}(\bar{X} - \mu)) \stackrel{d}{\rightarrow} T_p^2(n - 1)\\ \frac{1}{n - 1}T^2 = n(\bar{X} - \mu)'V^{-1}(\bar{X} - \mu) \stackrel{d}{\rightarrow} \frac{\chi^2(p)}{\chi^2(n-p)}\\ \frac{n - p}{(n - 1)p}T^2 \stackrel{d}{\rightarrow} \frac{\chi^2(p)/p}{\chi^2(n - p)/(n - p)} \stackrel{d}{\rightarrow} F(p, n - p)$$

则当未知时，的水平为的置信域估计为 :

$$D = \left\{\boldsymbol{\mu} \in \mathbb{R}^p : \frac{n(n - p)}{p}(\bar{X} - \boldsymbol{\mu})'V^{-1}(\bar{X} - \boldsymbol{\mu}) \leq F_{1 - \alpha}(p, n - p)\right\}$$

即有 .

PS: 因为这个置信域D是一个二次型，那么上述的不等式就是对这个二次型的约束，所以，这个置信域是一个超椭球。

• 协方差矩阵 的逆 定义了椭球的方向和形状，特征值决定了每个方向上的伸缩因子。
• 分布的临界值 确定了超椭球的大小。

B.两总体

设独立总体，，，。 (属于同一维度空间，但分布不同。)

记 ，分别为来自总体和的样本，。 我们要构造总体均值差的置信域估计。

已知：

已知条件	对应公式
样本X的样本离差阵和协方差矩阵
样本Y的样本离差阵和协方差矩阵

我们下面讨论的问题是：

1. : ①未知，②已知
2. （这种情况在本课程中不涉及，下面也不会涉及）

因此下面对于未知、已知的考虑的前提是.

已知

由，，有:

$$(\bar X-\bar Y)\overset{d}{\sim}N_p(\delta,(\frac1m+\frac1n)\Sigma)=N_p(\delta,\frac{mn}{m + n}\Sigma)$$

根据二次型的性质：,假设有个p阶方阵 ,则有. 当时, .

$$\frac{mn}{m + n}((\bar{X} - \bar{Y}) - \delta)'\Sigma^{-1}((\bar{X} - \bar{Y}) - \delta) \stackrel{d}{\rightarrow} \chi^2(p)$$

由此得到的水平为的置信域估计为:

$$D = \left\{\delta \in \mathbb{R}^p : \frac{mn}{m + n}((\bar{X} - \bar{Y}) - \delta)'\Sigma^{-1}((\bar{X} - \bar{Y}) - \delta) \leq \chi^2_{1 - \alpha}(p)\right\}.$$

未知

记和分别为总体和的样本离差阵。

由和的联合密度函数:

$$\begin{align} &(2\pi)^{-(m + n)p/2}|\boldsymbol{\Sigma}|^{-(m + n)/2} \cdot \\ &\exp\left\{-\frac{1}{2}\text{tr}[\boldsymbol{\Sigma}^{-1}(V_X + V_Y + m(\bar{X}-\boldsymbol{\mu}_1)(\bar{X}-\boldsymbol{\mu}_1)' + n(\bar{Y}-\boldsymbol{\mu}_2)(\bar{Y}-\boldsymbol{\mu}_2)')]\right\} \end{align}$$

知的极大似然估计为。

记，并令 :

$$T^2 = \frac{mn(m + n - 2)}{m + n}((\bar{X}-\bar{Y})-\boldsymbol{\delta})'V^{-1}((\bar{X}-\bar{Y})-\boldsymbol{\delta})$$

由于与相互独立，且

$$\sqrt{\frac{mn}{m + n}}((\bar{X}-\bar{Y})-\boldsymbol{\delta}) \stackrel{d}{\rightarrow} N_p(0,\boldsymbol{\Sigma}), \quad V \stackrel{d}{\rightarrow} W_p(m + n - 2,\boldsymbol{\Sigma})\\ T^2 \stackrel{d}{\rightarrow} T_p^2(m + n - 2)$$

进而可知

$$\begin{align} &\frac{m + n - p - 1}{(m + n - 2)p}T^2 \\ &= \frac{(m + n - p - 1)mn}{(m + n)(m + n - 2)p}((\bar{X}-\bar{Y})-\boldsymbol{\delta})'V^{-1}((\bar{X}-\bar{Y})-\boldsymbol{\delta}) \\ &\stackrel{d}{\sim} F(p,m + n - p - 1) \end{align}$$

由此得到的水平为的置信域估计为

$$D = \left\{ \boldsymbol{\delta} \in \mathbb{R}^p :\begin{align} \frac{(m + n - p - 1)mn}{(m + n)p}((\bar{X} - \bar{Y}) - \boldsymbol{\delta})'V^{-1}((\bar{X} - \bar{Y}) - \boldsymbol{\delta})\\ \leq F_{1 - \alpha}(p, m + n - p - 1)\end{align} \right\}$$

3.2.4 正态总体均值的Bayes估计

Bayes方法两要素：

1. 样本的密度函数形式已知、只是参数未知.
2. 参数也被视为随机变量，其密度函数（先验密度）完全确定.

先验密度如何确定？

1. 专业知识和专家经验.
2. 数学方法，如：共轭先验、Jeffery先验、无信息先验等.

A. Bayes推断

基于后验密度（分布）： 后验密度 ∝ 似然函数 × 先验密度

• 数据(样本)的似然函数为给定参数下的条件密度：
• 数据(样本)和参数的联合密度：
• 数据(样本)的边缘密度：
• Bayes后验密度为给定数据(样本)下参数的条件密度： .

$$p(\theta|X)=\frac{h(X, \theta)}{H(X)}=\frac{f(X|\theta)\pi(\theta)}{H(X)} \propto f(X|\theta)\pi(\theta)$$

逆Wishart分布

若，则称随机矩阵服从逆Wishart分布，记为，。

逆Wishart分布的密度函数 :

$$f_p(X)=\frac{|\boldsymbol{\Sigma}|^{-n/2}|X|^{-(n + p + 1)/2} \exp \left\{-\frac{1}{2} \text{tr}(\boldsymbol{\Sigma}^{-1} X^{-1})\right\}}{2^{(np/2)} \Gamma_p\left(\frac{n}{2}\right)}, \quad X>0$$

多元正态分布参数的先验分布

$$\begin{cases} \boldsymbol{\Sigma} \stackrel{d}{\sim} IW_p(\alpha, T) \\ \text{在} \boldsymbol{\Sigma} \text{给定的条件下}, \boldsymbol{\mu} \stackrel{d}{\sim} N_p(\boldsymbol{\theta}, k^{-1} \boldsymbol{\Sigma}) \end{cases}$$

其中，和为超参数。

后验密度

$$\pi_1(\boldsymbol{\Sigma} | \mathbf{X})=\frac{\left|\mathbf{T}_{n}\right|^{\alpha_{n} / 2}|\boldsymbol{\Sigma}|^{-\left(\alpha_{n}+p+1\right) / 2} \exp \left\{-\frac{1}{2} \operatorname{tr}\left(\mathbf{T}_{n} \boldsymbol{\Sigma}^{-1}\right)\right\}}{2^{\left(\alpha_{n} p / 2\right)} \pi^{p(p - 1) / 4} \prod_{i = 1}^{p - 1} \Gamma\left(\frac{\alpha_{n}-i + 1}{2}\right)}=I W_{p}\left(\alpha_{n}, \mathbf{T}_{n}\right) \\ \pi_2(\boldsymbol{\mu} | \boldsymbol{\Sigma}, \mathbf{X})=\frac{(2 \pi)^{-p / 2}|\boldsymbol{\Sigma}|^{-1 / 2} \exp \left\{-\frac{k n}{2(k + n)}(\boldsymbol{\mu}-\boldsymbol{\theta}_{n})^{\prime} \boldsymbol{\Sigma}^{-1}(\boldsymbol{\mu}-\boldsymbol{\theta}_{n})\right\}}{(2 \pi)^{p / 2}|\boldsymbol{\Sigma}|^{-1 / 2}}=N_{p}\left(\boldsymbol{\theta}_{n}, k_{n}^{-1} \boldsymbol{\Sigma}\right)$$

其中，

$$\alpha_{n}=n+\alpha, \quad \mathbf{T}_{n}=\mathbf{T}+\mathbf{V}+\frac{k n(\overline{\mathbf{X}}-\boldsymbol{\theta})(\overline{\mathbf{X}}-\boldsymbol{\theta})^{\prime}}{k + n}\\ \boldsymbol{\theta}_{n}=\frac{n \overline{\mathbf{X}}+k \boldsymbol{\theta}}{n + k}, \quad k_{n}=n + k$$

因此，该先验分布是共轭先验分布。

注：后验密度（分布）的形式一般都比较复杂，通常采用Markov chain Monte Carlo方法来计算。

Bayes估计

• Bayes估计 = 参数的后验均值
• 的Bayes估计：
• 的Bayes估计： (性质8)

作业1

设,i.i.d., 已知, 未知. 求的极大似然估计.

首先，我们知道这个答案是(雾)，然后开始写…

对于每个样本 ，其概率密度函数为：

$$f(X_i; \mu, \Sigma) = \frac{1}{(2\pi)^{p/2} |\Sigma|^{1/2}} \exp\left( -\frac{1}{2} (X_i - \mu)' \Sigma^{-1} (X_i - \mu) \right)$$

由于 是独立同分布的，因此样本的联合密度函数为：

$$L(\Sigma; X_1, X_2, \dots, X_n) = \prod_{i=1}^n f(X_i; \mu, \Sigma)\\ L(\Sigma; X_1, X_2, \dots, X_n) = \prod_{i=1}^n \frac{1}{(2\pi)^{p/2} |\Sigma|^{1/2}} \exp\left( -\frac{1}{2} (X_i - \mu)' \Sigma^{-1} (X_i - \mu) \right)\\ \ell(\Sigma; X_1, X_2, \dots, X_n) = \log L(\Sigma; X_1, X_2, \dots, X_n)\\ \ell(\Sigma; X_1, X_2, \dots, X_n) = -\frac{np}{2} \log(2\pi) - \frac{n}{2} \log|\Sigma| - \frac{1}{2} \sum_{i=1}^n (X_i - \mu)' \Sigma^{-1} (X_i - \mu)\\$$

为了求 的极大似然估计 ，我们对对数似然函数 关于 求导数，并令其等于零。

$$\frac{\partial}{\partial \Sigma} \log|\Sigma| = \Sigma^{-1}\\ \frac{\partial}{\partial \Sigma} \left( a \Sigma^{-1} b \right) = -\Sigma^{-1} a b' \Sigma^{-1}$$

$$\begin{align} \frac{\partial\ell}{\partial\Sigma}&=-\frac n2\Sigma^{-1}+\frac{1}{2}\sum^n_{i=1}\Sigma^{-1}(X_i-\mu)(X_i-\mu)'\Sigma^{-1}=0\\ n\Sigma^{-1}&=\sum^n_{i=1}\Sigma^{-1}(X_i-\mu)(X_i-\mu)'\Sigma^{-1}\\ \Sigma n\Sigma^{-1}\Sigma&=\sum^n_{i=1}\Sigma\Sigma^{-1}(X_i-\mu)(X_i-\mu)'\Sigma^{-1}\Sigma\\ n\Sigma &=\sum^n_{i=1}(X_i-\mu)(X_i-\mu)'\\ \hat{\Sigma} &= \frac{1}{n} \sum_{i=1}^n (X_i - \mu)(X_i - \mu)' \end{align}$$