多元统计分析-Ch1 多元分布
【挑战20天学完多元统计分析,让我们说:DDL是最佳生产力!】
Ch1 多元分布
[TOC]
1.0 预备知识
1.0.1 随机变量
随机变量
| 期望 | |
|---|---|
| 矩 | |
| 方差 |
1.0.2 随机向量
令
| 联合分布函数 | ||
|---|---|---|
| 联合概率密度函数(非负) | 存在 |
|
| 边缘分布 | (也就是选取随机向量中的部分、构成的分布)。 |
|
| 边缘概率密度函数 | 对 |
|
| 条件密度 | 令 |
X^{(1)}=x^{(1)})=\frac{f(x^{(1)},x^{(2)})}{g(x^{(1)})} |
1.0.3 多元随机变量(随机向量)
| 期望 |
|
|---|---|
| 协方差 |
|
| 协方差 |
1.0.4 矩阵知识
一些运算:
:期望和trace的计算等级相同。 :二次型,此公式将期望值分解为常数项(期望向量的二次型)和随机项(协方差矩阵与 A 的迹)。
分块矩阵:
记
记

1.0.5 多元特征函数
(特征函数与概率分布函数一一对应)随机向量
其中,
性质:
- 对正整数
, 如果 存在, 则 - 对
, 分量 的特征函数是 . - 记
的边缘特征函数分别为 , 记 的特征函数是 , 则 相互独立的充分必要条件是: . - 设
维随机向量 的特征函数分别为 , 如果 相互独立, 则随机向量和 的特征函数为: .
Q:我个人感觉这个地方是不是写错了?Y怎么会是p维向量?那角标不应该是p吗?
A: 在这里,
是独立的随机向量,每个 依然是 维的,所以 是多个 维向量
1.1 一元正态分布
【分布密度】若随机变量
其中$-\infty
1.2 多元正态分布
【分布密度】若
其中
d 代表服从分布(distribution),
是多元正态分布的方差。
p元标准正态分布:
定理1:设p元随机向量
证明:随机向量
的特征函数定义为: 其中,
是与 同维度的向量。 代入
到特征函数的定义中,得到: 由于
是 维标准正态随机向量, ,其特征函数为: 这里
是与 同维度的向量。 我们知道,一个
维正态分布 的特征函数为: 因此,
服从 分布,即: 如何产生
的(伪)随机数?—==Cholesky 分解== 生成的标准正态分布随机向量
可以通过下列变换得到目标分布 , L 是 Cholesky 分解得到的下三角矩阵,Z是标准正态随机向量。
1.2.2 性质
| 性质 | 说明: |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.密度函数 | $p(x)=(2\pi)^{-\frac p 2}\ | \Sigma\ | ^{-\frac 1 2}\exp\left\{-\frac 1 2 (x-\mu)’\Sigma^{-1}(x-\mu)\right\}$ | ||||||
| 2.特征函数 | |||||||||
| 3.期望方差 | |||||||||
| 4.线性变换 | |||||||||
| 5.相互独立 | 设 |
||||||||
| 6.卡方分布 | |||||||||
| 7.矩阵分解 | |||||||||
| 8.分量独立性 | |||||||||
| 9.条件分布 | $(X_1 | X_2=x_2)\overset{d}{\sim}N_q(\mu_{1 | 2},\Sigma_{1 | 2}) |
2}=E(X_1 | X_2=x_2)=\mu_1+\Sigma_{12}\Sigma_{22}^{-1}(x_2-\mu_2) |
2}=Cov(X_1 | X_2=x_2)=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21} |
2}\le\Sigma_{11})$ |
| 10.变量的独立分解 | 令 |
1}) |
2} |
1}=\Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12})$ |
1.3 相关系数
| 定义 | 说明 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 相关系数 |
||||||||||||
| 相关矩阵R | ||||||||||||
| 偏相关系数 | X_2^{(p-q)})\overset{d}{\sim}N_q(\mu_{1 | 2},\Sigma_{1 | 2}) |
(1 | 2)}=\frac{\sigma_{(ij) | (1 | 2)}}{\sqrt{\sigma_{(ii) | (1 | 2)}}\sqrt{\sigma_{(jj) | (1 | 2)}}}$ | |
| 精度矩阵 |
设随机向量 |
偏相关系数是图模型和因果推断中的重要统计量,可以由特征函数+期望+方差,可以通过偏相关系数判别多元正态随机向量分量之间的条件独立性。
精度矩阵的性质:
若
在
证明:
由(分量独立性):
则
无量纲:因为精度矩阵的数值与变量的量纲有关,所以进行标准化处理。令
在给定
1.3.1 练习
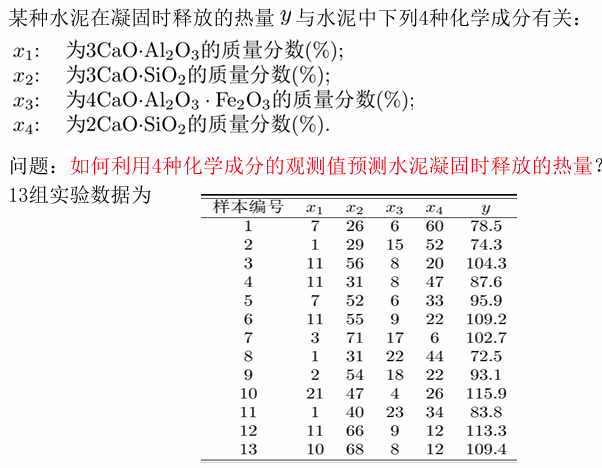
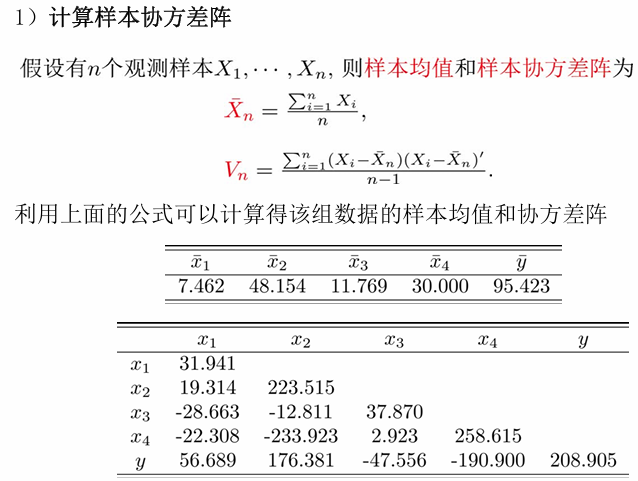
对于
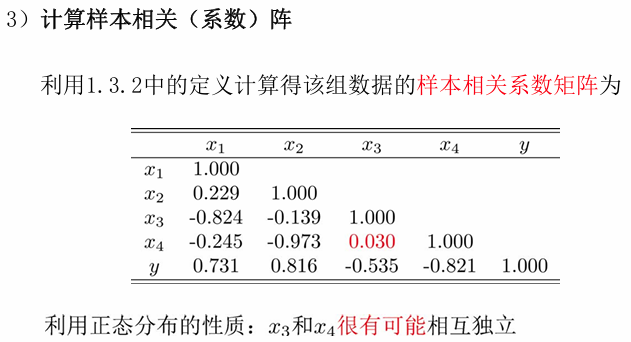
预测:计算y关于
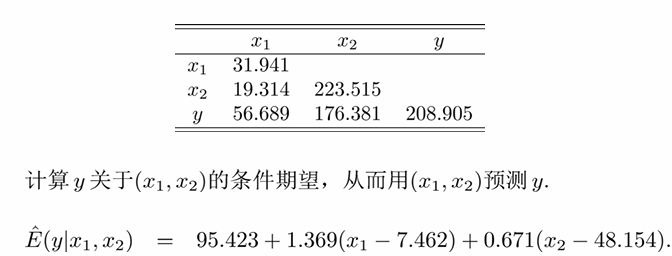
1.4 矩阵多元正态分布
1.4.0 矩阵拉直和Kronecker积
矩阵拉直:记
Kronecker积:令
令
令
的计算步骤如下:
拉直运算和Kronecker积的性质
| 性质 | 说明 |
|---|---|
| 1 | 对任意实数 |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | 若 |
| 7 | |
| 8 | 若 |
| 9 | 若 |
1.4.1 矩阵分布
设
记
随机矩阵的期望:
矩阵的拉直运算:
随机矩阵的协方差阵:
随机矩阵的分布:随机矩阵拉直后的随机向量的分布。
矩阵
即
是因为
独立同分布,所以它们的 都是一样的。
随机矩阵拉直运算的性质(转置)
性质1:对
其中,
由性质1,对上述随机矩阵
因此,对由
1.4.3 矩阵正态分布
矩阵正态分布是指矩阵的每一列或每一行都服从正态分布,且这些列或行之间可能具有某种协方差结构。
矩阵正态分布的一个重要特性是它的“拉直”形式也是正态分布。
假设矩阵
- 如果
一般地,记
从这个分布,可以得到
密度函数
矩阵正态分布的密度函数表示了矩阵
若
上式等价于(用迹的性质进行简化):
证明:(即证
利用Kronecker积的一个重要性质:
其中 、 和 分别是 、 和 的矩阵。
线性变换
如果矩阵服从正态分布,经过线性变换后,结果仍然服从矩阵正态分布,只是均值和协方差矩阵发生了变化。
性质2:设
对其进行线性变换
则矩阵