Schwertlilien
归档分类标签关于
搜索
归档分类标签关于
Schwertlilien
As a recoder: notes and ideas.

2023.3.27

每天の学习日记数据结构
版权声明: 署名-非商业性使用-禁止演绎 4.0
全文约2.5K字
阅读次数:

2023.3.27—图のreview

今天早上修复了blog：

原先出现的问题是：在上传文件后对文件进行了修改，可能导致CSS渲染文件或者js文件出错。然后hexo寄了。

修复的方法是：Hexo的安装及重置恢复_怪异收集者的博客-CSDN博客。所以change一个主题，然后就好啦！但是需要自己 改一下config.yml(也可以把之前的copy一下放到新的主题文件夹内)，但是我干脆就换了一个了。

看看现在的：

图的概念

简单图：无自环，无重边。

子图：边的子集，以及相关联的点集。

度(Degree)

在无向图中，顶点的度是其邻接点的数目。

在有向图中。(入度)指向这个顶点的弧的数目，(出度)此顶点指向其他顶点的弧的数目。该顶点的度=出度+入度。

邻接与路径

在无向图中，存在一条边(u,v)：则称u和v邻接。

在有向图中，存在一条边：则v是u的邻接点。

路径：图上一个顶点序列，其中序列上任意相邻两点都邻接。

简单路径：顶点和边==不重复出现==。

环：除了顶点和终点相同外没有重复顶点的路径。

连通和连通分量

连通(connected)：如果无向图中任意两点都有路径，则图是连通的；否则是非连通的。

非连通图有多个连通分量。==连通与非连通是无向图上的概念，有向图是强连通和弱连通。==

强连通图：有向图中任意两点都有相互可达的路径。

相互可达的子图属于同一个强连通分量(scc)。

树(连通无向无环图)

==树可以 以任意点作为根==。

下面是一些定理：

  • G上有V个点，有V-1条边，还是一个无环图，那么它一定是连通的。

    反过来也成立：G上有V个点，有V-1条边，还是连通的，那么它一定是无环图。

  • G连通，但认一删除一条边后不连通。

    G无环，但任意添加一条边后包含环。

  • 任意两点只有唯一的简单路径。

    简单路径：顶点和边==不重复出现==。

稀疏图与稠密图

如何划分稀疏图与稠密图？假设考虑有向图：G=那么$E=V^2$数量级是稠密图。

  • 稀疏图：边数E和$\frac {V(V-1)}{2}$相比非常少(V,E同数量级)
  • 时间复杂度为$O(ElogE)$和$O(V^2)$的算法：对稀疏图来说前者好，对稠密图来说后者好。

欧拉路径与欧拉回路

欧拉路径：只通过每条边一次的路径。

欧拉回路：如果这条路径的起点和终点是同一点。

一笔画问题。

  • 对无向图：图G有一条欧拉路径，当且仅当G是连通的，且有0 or 2 个奇度数节点。当所有节点都是偶度数时欧拉回路七点可以是任意点。
  • 对有向图：存在欧拉路径的条件：图连通，所有点出度=入度，or 有一个终点的入度-出度=1，一个起点的出度-入度=1。当所有点出度=入度是任意点可作为起点，而后者必须以出度-入度=1的点作为起点，入度-出度=1的点作为终点。

图的存储

边列表

基本上题目给出的就是这种形式，但是这种形式并不是很好处理。

邻接矩阵

1
int G[2005][2005];//G[u][v]:u->v的边

邻接表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//====================[vector实现]==================================//
//由于起点知道，所以只存储终点。
struct Edge{//1->2->5:1与2,1与5之间存在边。
    int end;
    int weight;
    Edge(int v,int w):end(v),weight(w){}//构造函数
};

vector<Edge> adj[N+5];//N:点的个数

//Input
for(int i=1;i<=M;i++){
    int u,v,w;
    cin>>u>>v>>w;
    adj[u].push_back(Edge(v,w));
    adj[v].push_back(Edge(u,w));//如果是无向图需要双向建边。
}

//====================[链表实现--链式前向星]===========================//
const int maxN=5e5+5;

struct Edge{
    int to;
    int weight;
    Edge* next;
};

Edge pool[maxN*2];
int heads[maxN];
int nn;

void addEdge(int from,int to,int weight){
    pool[++nn].to=to;
    pool[nn].weight=weight;
    pool[nn].next=heads[from];
    heads[from]=nn;
}

前向星

以储存边的方式来存储图。构造方法如下：读入每条边的信息，将边存放在数组中，把数组中的边按照起点顺序排序(可以使用基数排序，如下面例程)，前向星就构造完了。通常用在点的数目太多，或两点之间有多条弧的时候。

一般在别的数据结构不能使用的时候才考虑用前向星。除了不能直接用起点终点定位以外，前向星几乎是完美的。

把边集数组终得每一条边按照起点大小排序，如果起点相同就按照终点从小到大排序。并记录下以i为起点的起始位置和以i为起点的边数(i的出度)。

  • head[i]：记录以i为边集在数组终得第一个存储位置。

  • len[i]：记录所有以i为起点的边在数组终得存储长度。

链式前向星—静态邻接表

1
2
3
4
5
6
7
8
9
10
11
12
13
struct Edge{
    int next;	//与第i条边同起点的下一条边的存储位置
    int to;		//第i条边的终点
    int w;		//边权
};

void addEdge(int u,int v,int w){
    e[cnt].to=v;
    e[cnt].w=w;
    e[cnt].next=head[u];//以u为起点的最后一条边的编号
    head[u]=cnt++;		//更新以u为起点的上一条边的编号=head[u]=cnt;cnt++;
}//实际上是模拟的邻接表的将新节点从head插入：next=head[u];
//head[]:表示以i为起点的第一条边存储的位置

P5318

小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$）以及 $m(m\le10^6)$ 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

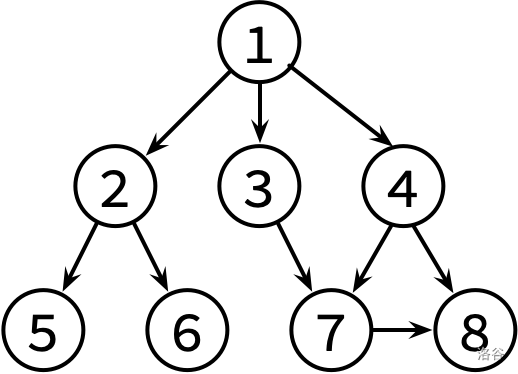
这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
# include<bits/stdc++.h>
using namespace std;

const int maxN = 1e5 + 5;
const int maxM = 1e6 + 5;
int n, m, cnt;
vector<int> adj[maxN];
bool vis_dfs[maxN] = {0};

bool vis_bfs[maxN] = {0};

void dfs(int x) {
	vis_dfs[x] = true;
	cout << x << " ";

	for (int i = 0; i < adj[x].size(); i++) {
		int node = adj[x][i];
		if (!vis_dfs[node])
			dfs(node);
	}

}

void bfs(int x) {//广搜需要借助队列
	queue<int>q;
	q.push(x);
	cout << endl << x << " ";
	vis_bfs[x] = true;

	while (!q.empty()) {
		int node = q.front();
		for (int i = 0; i < adj[node].size(); i++) {
			int end_node = adj[node][i];
			if (!vis_bfs[end_node]) {
				vis_bfs[end_node] = true;
				q.push(end_node);
				cout << end_node << " ";
			}
		}
		q.pop();
	}
}


int main() {
	int u, v;

	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		cin >> u >> v;
		adj[u].push_back(v);
	}

	for (int i = 1; i <= n; i++) {
		sort(adj[i].begin(), adj[i].end());
	}

	dfs(1);//我对这个地方有点疑问：1号点一定会有edge吗？
	bfs(1);
	return 0;
}

P3916

给出 $N$ 个点，$M$ 条边的有向图，对于每个点 $v$，求 $A(v)$ 表示从点 $v$ 出发，能到达的编号最大的点。

好吧，看这个题并不是很难，所以速速的就完了。但是T了一个点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# include<bits/stdc++.h>
using namespace std;

const int maxN = 1e5 + 5;
int n, m, cnt;
vector<int> adj[maxN];
bool vis_dfs[maxN] = {0};

void dfs(int x) {
	vis_dfs[x] = true;
	if (x > cnt)
		cnt = x;
	for (int i = 0; i < adj[x].size(); i++) {
		int node = adj[x][i];
		if (!vis_dfs[node])
			dfs(node);
	}
}

int main() {
	int u, v;
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		cin >> u >> v;
		adj[u].push_back(v);
	}

	for (int i = 1; i <= n; i++) {
		cnt = 0;
		memset(vis_dfs, 0, sizeof(vis_dfs));
		dfs(i);
		cout << cnt << " ";
	}
}

看了看题解，主要的思路是反向建边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# include<bits/stdc++.h>
using namespace std;

const int maxN = 1e5 + 5;
int n, m, cnt;
vector<int> adj[maxN];
int vis[maxN] = {0};

void dfs(int x, int d) {
	if (vis[x]) //--|
		return; //	|--主要就是这里：由于是从最大开始遍历，那么直接赋值就是max，那么可以直接返回。
	vis[x] = d; //--|
	for (int i = 0; i < adj[x].size(); i++) {
		int node = adj[x][i];
		if (!vis[node])
			dfs(node, d);
	}
}

int main() {
	int u, v;
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		cin >> u >> v;
		adj[v].push_back(u);//反向建边--主要是配合上面的步骤
	}

	for (int i = n; i ; i--) {
		dfs(i, i);
	}

	for (int i = 1; i <= n; i++)
		cout << vis[i] << " ";
}

P1807

设 $G$ 为有 $n$ 个顶点的带权有向无环图，$G$ 中各顶点的编号为 $1$ 到 $n$，请设计算法，计算图 $G$ 中 $1, n$ 间的最长路径。

乐，没写完，明天再说。

搜索
匹配结果数:
未搜索到匹配的文章。