2023.3.14

今天有三节课，但是没事，可以翘。

今天有算法分析作业。

[TOC]

record一下：

动态规划

为什么使用递归求斐波纳契数列很慢？

复杂度是$2^n$（大概），多个重叠子问题，重复计算。使用空间换时间，避免重复计算。

我算fib(5) -> fib(3) + fib(4) -> fib(1)+fib(2) + fib(2)+fib(3)

Basic idea

• 保存子问题的结果，避免重复计算。
• 用额外的数据保存（备忘录memo）
• 空间换时间
• 大问题可以由子问题推出（状态转移）我个人感觉很像分治

int memo[10005];
int fib(int n){//[递归+备忘]
    if(memo[n]!=0)return memo[n];
    if(n==1||n==2)return memo[n]=1;
    return memo[n]=fib(n-1)+fib(n-2);
}//时间复杂度O(n)

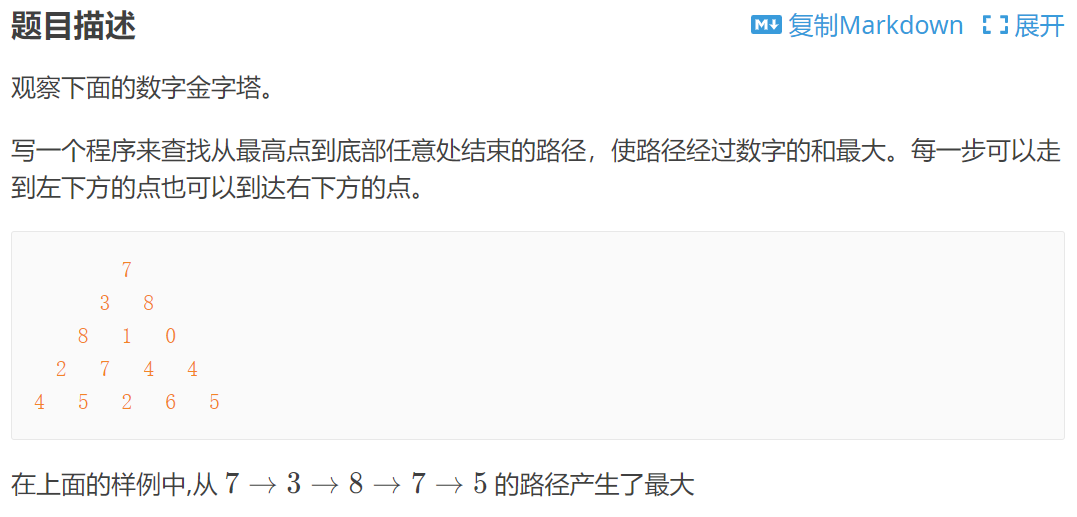
P1216

递归：$d(r,j)$表示第r行，第j个数（r,j从1开始）

maxSum(r,j):表示从(r,j)位置到底表最优路线和。
$$
maxSum(r,j)=\begin{cases}
d(r,j)&r=n\
Max(maxSum(r+1,j),maxSum(r+1,j+1))+d(r,j)&r\ne n\
\end{cases}
$$

const int MAXN=1005;
int d[MAXN][MAXN];
int n;
int maxSum(int r,int j){
    if(r==n)return d[r][j];
    int x=maxSum(r+1,j);
    int y=maxSum(r+1,j+1);
    return max(x,y)+d[r][j];
}//也可以把求过的点存下来

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){cin>>d[r][j];}
    }//感觉可以优化的地方有很多，这里使用的二维数组，可以压缩成一维的。
    cout<<maxSum(1,1)<<endl;
}

使用MEMO：

int memo[MAXN][MAXN];

int maxSum(int r,int j){
    if(memo[r][j]!=-1)return memo[r][j];
    if(r==n)return memo[r][j]=d[r][j];
    int x=maxSum(r+1,j);
    int y=maxSum(r+1,j+1);
    return memo[r][j]=max(x,y)+d[r][j];
}

int main(){
    cin>>n;
    memset(memo,-1,sizeof(memo));
    for(int i=1;i<=n;i++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){cin>>d[i][j];}
        }
    }
    cout<<maxSum(1,1)<<endl;
    return 0;
}

上面的这种方法是自顶向下的：在main函数内是maxSum(1,1)从第一行第一个元素开始。

我们也可以选择从下往上填MEMO。

递推+填表

7					|	30
3	8				|	23	21
8	1	0			|	20	13	10
2	7	4	4		|	7=max(4,5)+2	12	10	10
4	5	2	6	5	|	4	5	2	6	5

int memo[MAXN][MAXN];
int d[MAXN][MAXN];

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){//输出数组
        for(int j=1;j<=i;j++){cin>>d[i][j];}
    }
    
    for(int i=1;i<=n;i++){memo[n][i]=d[n][i];}//把最后第n层给预备好。
    
    for(int i=n-1;i;i--){//自底向上，从倒数第二层开始。
        for(int j=1;j<=i;j++){//确保在memo这里不会越界。
            memo[i][j]=max(memo[i+1][j],memo[i+1][j+1])+d[i][j];
        }
    }
    cout<<memo[1][1]<<endl;
}

可以看到，上面会使用到二维数组。但是我们实际上只填了一半，比较浪费。可以优化成一维数组。先可以把memo的二维数组变成一维（一行n）。

basic idea:

主要是求完memo[r][j]后memo[r+1][j]就不再使用，因此可以用memo[r][j]覆盖memo[r+1][j]。

int memo[MAXN];//压缩成一维。
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){cin>>d[i][j];}
    }
    for(int i=1;i<=n;i++){memo[i]=d[n][i];}
    for(int i=n-1;i;i--){
        for(int j=i;j<=i;j++){
            memo[j]=max(memo[j],memo[j+1])+d[i][j];
        }
    }
    cout<<memo[1]<<endl;
}

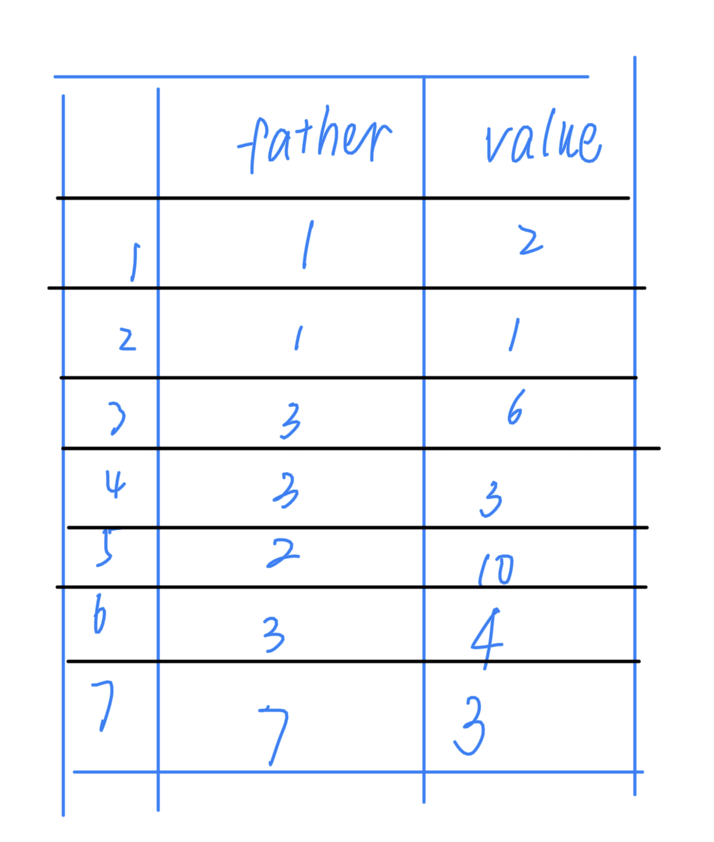
P2 训练计划

这题乍看是个DP，但是实际上应该是计算图以及最短路。（感觉并查集就好了）

//input
void input(){
	int course[105][2];//[1]:father,[2]:day
    int n,m;//距离大赛开幕的天数和训练科目的数量
    cin>>n>>m;
    for(int i=1;i<=m;i++){//填充并查集
        cin>>course[i][0];
        if(!course[i][0])course[i][0]=i;
    }
    for(int i=1;i<=m;i++){//填充value
        cin>>course[i][1];
    }
}

计算每科的最早开始时间；计算完之后计算maxTime>n时，就不往后计算了。否则就要逆推得到每科的最晚开始时间。

int find(int i){
    if(earliest_time[i]!=-1)return earliest_time[i];
    if(course[i][0]==i)return earliest_time[i]=1;
    int father=course[i][0];
    return earliest_time[i]=find(a)+course[a][1];
}

int main(){
    iuput();
    //计算最早开始时间--
    //大概的想法是if(father[a]==a)那么a科不存在依赖，最早开始时间是一天。
    //然后对于有依赖关系的，通过find找，但是在递归的过程中可以+路径，最后return 总路径
    int earliest_time[m];
    memset(earliest_time,-1,sizeof(earliest_time));
    for(int i=1;i<=m;i++){
        cout<<find(i)<<" ";
    }
}

测试是否会超过给的时间：

//test over the given time
for(int i=1;i<=m;i++){
    if(earliest_time[i]+course[i][1]>n)return 0;
}

//latest_time
int latest_time[105];

int find_late(int i){
    if(latest_time[i]!=-1)return latest_time[i];
    if(course[i][0]==i)return latest_time[i]=(n+1-course[i][1]);
    int fa=course[i][0];
    return latest_time[i]=find_late(fa)-course[i][1];
}

算法分析作业

每个子问题的规模都一样，且相对于父问题都是成比例缩小。
$$
T(n)=aT(\frac n 2)+f(n)
$$